PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Farhod
Tester: Joud Zouzou
Editorialist: Taranpreet Singh
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Reachability Tree, Disjoint Set Union, Sortings and Observations.
PROBLEM:
Given N planets numbered from 1 to N with associated gain values given in array A and M bidirectional spaceways, each spaceway connecting two different planets u and v and require at least w status level. At visiting any planet x for the first time in a query, your current status level increases by A_x.
For Q queries giving the source planet, x and destination planet y, find out the minimum status level L \geq 0 required at the start time to reach from x to y, or determine it is impossible to reach to planet y for any status level at the start point. Each query is independent of each other.
QUICK EXPLANATION
- Sorting the spaceways in non-decreasing order of status requirement, we know that if we can use the current spaceway, we can use all the previous spaceways.
- Let us maintain a disjoint set union, initially each node being in its own disjoint set, and for each storing an additional value V initially zero, representing the minimum status needed to start from
EXPLANATION
Let us build reachability tree with 2*N-1 nodes where N planets become the leaves of reachability tree and all the edges in minimum spanning forest (considering status level as weight) representing an internal node in reachability tree. The Tree is organized in such a way such that for each internal node, the subtree of this node contains the largest set of nodes which are reachable using spaceways of status requirement up to x.
Consider an example with 6 planets and following spaceways (Given in sorted order of status)
2 3 with requirement 2
2 4 with requirement 3
4 5 with requirement 4
1 4 with requirement 5
The reachability tree for above is shown in the following image.
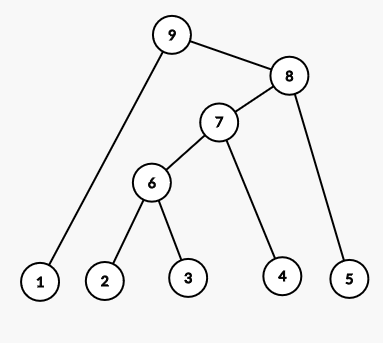
We can see,
- all nodes in subtree of 6 can be visited using spaceways of requirement up to 2.
- all nodes in subtree of 7 can be visited using spaceways of requirement up to 3.
- all nodes in subtree of 8 can be visited using spaceways of requirement up to 4.
- all nodes in subtree of 9 can be visited using spaceways of requirement up to 5.
Let’s consider edges in non-decreasing order of status requirements. Now, when we reach for spaceway from 2 to 4 with requirement 3, we have already created fictitious node 6 and can reach node 2 to node 3.
Coming to answering queries, let us find the LCA of x and y in the reachability tree. For example, suppose we need to calculate the minimum beginning status requirement to move from 2 to 4. We see that LCA(2,4) = 7. In order to reach from 2 to 4, we shall only use spaceways with status requirement up to 3, since node 7 contain only nodes reachable from each other using spaceways of status requirement 3.
Suppose we need L status at beginning. Current status at node 2 becomes L+A_2. If L+A_2 \geq 3 > 2, so we can also visit planet 3, which increases our status requirement to L+A_2+A_3 \geq L+A_2. So, it is always beneficial to visit all planets reachable using spaceways with status requirement up to maximum status requirement spaceway needed to reach from x to y, as we only increase status. So, minimum status requirement is max(2-(A_2), 3-(A_2+A_3)).
Similarly, minimum status requirement to reach node 1 from node 3 is max(2-A_3, 3-(A_2+A_3), 4-(A_2+A_3+A_4), 5-(A_2+A_3+A_4+A_5)). If we see carefully, the answer to query from x to y is the maximum of (W_p-S_p) where p is every ancestor of x including x, but excluding LCA(x, y) in reachability tree where W_p is the status requirement of spaceway of parent of p and S_p is the sum of gain of all leaf nodes in subtree of p.
Of course, if nodes aren’t reachable from each other using any spaceway, the answer is -1. Don’t forget to keep L \geq 0 if an answer exists. Refer implementation if any doubts.
TIME COMPLEXITY
The time complexity of above solution is O(N* α(N) + M*logM + Q*log(N)) or O(N* α(N) + M*logM + Q*log^2(Q)) depending upon implementation (Fast and Slow implementations given below.)
SOLUTIONS:
Setter's Solution (Fast Implementation)
#include <bits/stdc++.h>
#define fi first
#define se second
const int N = 200200;
using namespace std;
int n;
int m;
int tim;
int p[N];
int dip[N];
int tin[N];
int tout[N];
int f[N][19];
int d[N][19];
long long a[N];
bool root[N];
vector < pair < int, int > > v[N];
int get(int x)
{
return x == p[x] ? x : p[x] = get(p[x]);
}
void dfs(int x, int p)
{
tin[x] = ++tim;
f[x][0] = p;
for(int i = 1; i < 19; i++){
f[x][i] = f[f[x][i - 1]][i - 1];
d[x][i] = max(d[x][i - 1], d[f[x][i - 1]][i - 1]);
}
for(auto y: v[x]){
dip[y.fi] = dip[x] + 1;
d[y.fi][0] = y.se;
dfs(y.fi, x);
}
tout[x] = tim;
}
bool isp(int x, int y)
{
return tin[x] <= tin[y] && tout[x] >= tout[y];
}
int lca(int x, int y)
{
if(isp(x, y)){
return x;
}
if(isp(y, x)){
return y;
}
for(int i = 18; i >= 0; i--){
if(!isp(f[x][i], y)){
x = f[x][i];
}
}
return f[x][0];
}
int get_res(int x, int g)
{
int res = 0;
for(int i = 0; i < 19; i++){
if(g & (1 << i)){
res = max(res, d[x][i]);
x = f[x][i];
}
}
return res;
}
void solve()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
vector < pair < int, pair < int, int > > > e;
for(int i = 1; i <= m; i++){
int x, y, w;
scanf("%d%d%d", &x, &y, &w);
e.push_back({w, {x, y}});
}
sort(e.begin(), e.end());
int G = n + 1;
for(int i = 1; i <= n + n; i++){
v[i].clear();
p[i] = i;
root[i] = true;
dip[i] = 0;
}
for(auto pe: e){
int x = pe.se.fi, y = pe.se.se;
long long w = pe.fi;
x = get(x);
y = get(y);
if(x == y){
continue;
}
v[G].push_back({x, max(0ll, w - a[x])});
v[G].push_back({y, max(0ll, w - a[y])});
p[x] = G;
p[y] = G;
a[G] = a[x] + a[y];
root[x] = root[y] = false;
G++;
}
tim = 0;
for(int i = 1; i < G; i++){
if(root[i]){
for(int j = 0; j < 19; j++){
d[i][j] = 0;
}
dfs(i, i);
}
}
int q;
scanf("%d", &q);
for(int i = 1; i <= q; i++){
int x, y;
scanf("%d%d", &x, &y);
if(x == y){
printf("0\n");
} else if(get(x) != get(y)){
printf("-1\n");
} else{
int p = lca(x, y);
printf("%d\n", get_res(x, dip[x] - dip[p]));
}
}
}
int main()
{
//freopen("sample.in", "r", stdin);
//freopen("sample.out", "w", stdout);
ios_base::sync_with_stdio(0);
int T;
scanf("%d", &T);
while(T--){
solve();
}
}
Tester's Solution
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <string>
#include <assert.h>
using namespace std;
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
assert(cnt>0);
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
cerr<<(int) g<<endl;
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
long long g=readInt(l,r,'\n');
return g;
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
struct edge{
int u,v,w;
};
bool operator<(edge a, edge b){
return a.w<b.w;
}
int T;
int n,m,q;
int sm_n=0;
int sm_m=0;
int sm_q=0;
int A[100100];
edge list[100100];
int pa[100100];
int root(int a){
if(pa[a]==a)return a;
return pa[a]=root(pa[a]);
}
void merge(int a,int b){
a=root(a);
b=root(b);
if(a!=b){
pa[a] = b;
}
}
bool is_samee(int a,int b){
return root(a)==root(b);
}
vector<int> adj[100100];
vector<int> cst[100100];
bool vis[100100];
int main(){
//freopen("3.in.txt","rb",stdin);
T=readIntLn(1,100);
while(T--){
n=readIntSp(1,100000);
m=readIntLn(1,100000);
for(int i=1;i<=n;i++){
pa[i]=i;
adj[i].clear();
cst[i].clear();
}
sm_n += n;
assert(sm_n<=400000);
sm_m += m ;
assert(sm_m<=400000);
for(int i=1;i<=n;i++){
if(i==n){
A[i]=readIntLn(0,1000000000);
} else {
A[i]=readIntSp(0,1000000000);
}
}
int mxxx =0;
for(int i=0;i<m;i++){
int u,v,w;
u=readIntSp(1,n);
v=readIntSp(1,n);
w=readIntLn(0,1000000000);
mxxx=max(mxxx,w);
list[i].u=u;
list[i].v=v;
list[i].w=w;
}
sort(list,list+m);
for(int i=0;i<m;i++){
if(!is_samee(list[i].u,list[i].v)){
adj[list[i].u].push_back(list[i].v);
cst[list[i].u].push_back(list[i].w);
adj[list[i].v].push_back(list[i].u);
cst[list[i].v].push_back(list[i].w);
merge(list[i].u,list[i].v);
}
}
q=readIntLn(1,100000);
sm_q+=q;
assert(sm_q <= 400000);
for(int i=0;i<q;i++){
int x,y;
x=readIntSp(1,n);
y=readIntLn(1,n);
if(!is_samee(x,y)){
cout<<-1<<endl;;
continue;
}
priority_queue<pair<int,int> > p;
for(int i=1;i<=n;i++){
vis[i]=false;
}
vis[x]=true;
p.push(make_pair(0,x));
int stat=0;
int sol =0 ;
while(!p.empty()){
pair<int,int> nd=p.top();
p.pop();
nd.first *= -1;
int need = max(0,nd.first - stat);
sol += need;
stat += need;
stat += A[nd.second];
if(stat >= mxxx)break;
if(nd.second == y)break;
for(int i=0;i<adj[nd.second].size();i++){
int ch=adj[nd.second][i];
int co=cst[nd.second][i];
if(vis[ch])continue;
vis[ch]=true;
p.push(make_pair(-co,ch));
}
}
cout<<sol<<endl;
}
}
assert(getchar()==-1);
}
Editorialist's Solution (Slow Implementation)
import java.util.*;
import java.io.*;
import java.text.*;
public class Main{
//SOLUTION BEGIN
//This code is not meant for understanding, proceed with caution
void pre() throws Exception{}
void solve(int TC) throws Exception{
int n = ni(), m = ni();
int SZ = 2*n-1;
TreeSet<Integer>[] qset = new TreeSet[SZ];
int[] set = new int[SZ], sz = new int[SZ];
long[] a = new long[SZ];
for(int i = 0; i< n; i++)a[i] = nl();
int[][] e = new int[m][];long[] w = new long[m];
for(int i = 0; i< m; i++){
e[i] = new int[]{ni()-1, ni()-1, i};
w[i] = nl();
}
long[] cost = new long[SZ];
for(int i = 0; i< SZ; i++){
set[i] = i;sz[i] = 1;
qset[i] = new TreeSet<>();
}
int q = ni();
int[] st = new int[q];//Start node of query
long[] ans = new long[q];//Answer to queries
Arrays.fill(ans, -1);
for(int qq = 0; qq< q; qq++){
int x = ni()-1, y = ni()-1;
if(x==y){
ans[qq] = 0;
continue;
}
st[qq] = x;
qset[x].add(qq);
qset[y].add(qq);
}
Arrays.sort(e, (int[] i1, int[] i2)->{
return Long.compare(w[i1[2]], w[i2[2]]);
});
int nxt = n;
//Answer of queries
for(int i = 0; i< m; i++){
int x = e[i][0], y = e[i][1];
long we = w[e[i][2]];
x = find(set, cost, x);
y = find(set, cost, y);
//If x and y already reachable using previous edges
if(x==y)continue;
if(sz[x]<sz[y]){int t = x;x=y;y=t;}
//Updating cost for moving from x to y
cost[x] = Math.max(cost[x], we-a[x]);
//Updating cost for moving from y to x
cost[y] = Math.max(cost[y], we-a[y]);
//Created new node and made it parent of both roots of components
set[x] = nxt;
set[y] = nxt;
//Updated size and values for each
a[nxt] = a[x]+a[y];
qset[nxt] = qset[x];
a[nxt] = a[x]+a[y];
sz[nxt] = sz[x]+sz[y];
//Iterating over smaller set
for(Integer idx:qset[y]){
if(qset[nxt].contains(idx)){
//Finding max over path from start of query to nxt
find(set, cost, st[idx]);
//answering query
ans[idx] = cost[st[idx]];
qset[nxt].remove(idx);
}else qset[nxt].add(idx);
}
nxt++;
}
for(long l:ans)pn(l);
}
int find(int[] set, long[] cost, int x){
if(set[x] != x){
//Finding tomost parent
int p = find(set, cost, set[x]);
//Updating cost to max of current cost and cost from p to set[x]
cost[x] = Math.max(cost[x], cost[set[x]]);
set[x] = p;
}
return set[x];
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
long mod = (long)1e9+7, IINF = (long)1e18;
final int INF = (int)1e9, MX = (int)2e5+1;
DecimalFormat df = new DecimalFormat("0.00000000000");
double PI = 3.1415926535897932384626433832792884197169399375105820974944, eps = 1e-8;
static boolean multipleTC = true, memory = false;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
if(memory)new Thread(null, new Runnable() {public void run(){try{new Main().run();}catch(Exception e){e.printStackTrace();}}}, "1", 1 << 28).start();
else new Main().run();
}
long gcd(long a, long b){return (b==0)?a:gcd(b,a%b);}
int gcd(int a, int b){return (b==0)?a:gcd(b,a%b);}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()