RAMDEV - Editorial

editorial
, , , , , ,
1

PROBLEM LINK:

International Day of Yoga

Author and Editorialist: Kabir Kanha Arora
Testers: Illisha Singh, Jackson Jose, Nishank Suresh, Vaibhav Gautam

DIFFICULTY:

EASY - MEDIUM

PREREQUISITES:

Observation, Greedy.

PROBLEM:

Given a rectangular yoga mat and N halls, how many mats can you fit in all the halls combined, if all the mats have to be aligned axis-parallel to the hall, and all the mats in any given hall have the same orientation?

DEFINITIONS:

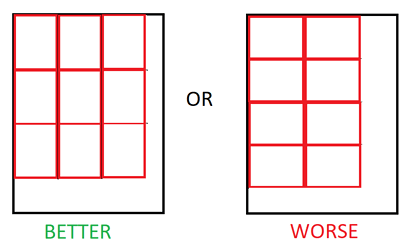
  • Let us first explain what axis-parallel means. According to Wikipedia, In geometry, an axis-parallel object is an object in n-dimensional space whose shape is aligned with the coordinate axes of the space.
    The following diagram helps illustrate that:
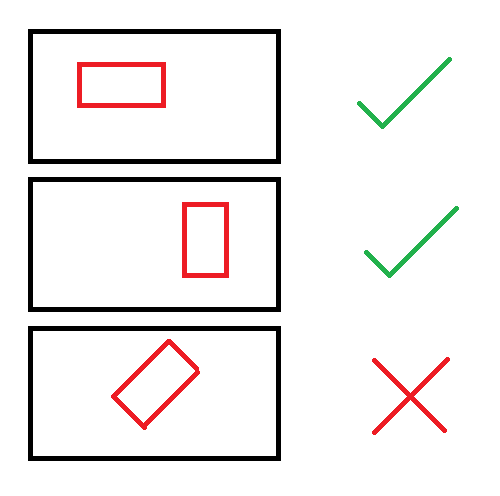
    AxisParallel

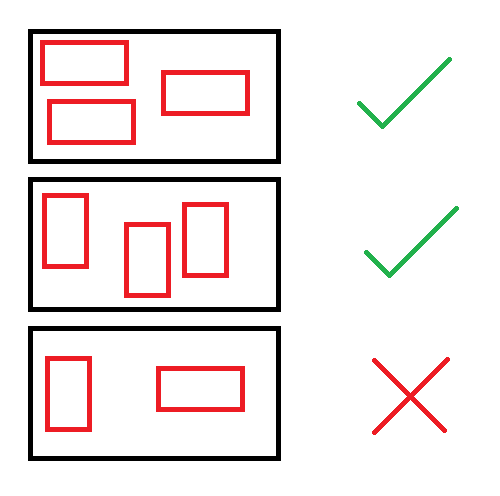
  • Secondly, it is important that you understand what having the same orientation in one hall means. The following diagram explains that:
    ValidConfigs

EXPLANATION:

You will observe that we can look at each of the N halls separately and independently. You will also observe that it is optimal, and can be proved, to arrange the yoga mats starting from one of the corners, in the following manner:

Optimal
Optimal880×529 4.74 KB

Now we just need to look at the number of yoga mats both of these arrangements allow us to place, and pick the better one.

\implies So, if a given hall is of dimension L_i \times B_i and the yoga mats have dimensions l \times b, then we can place \lfloor \frac{L_i}{l} \rfloor \times \lfloor \frac{B_i}{b} \rfloor mats in one of the arrangements, and \lfloor \frac{L_i}{b} \rfloor \times \lfloor \frac{B_i}{l} \rfloor in the other. The optimal answer is simply the max of these two.

This process is then repeated across all the halls and the answer is summed up.

COMMON ERRORS:

  • Dividing the area of a hall by the area of a yoga mat.
    This simply won’t work. Consider the case where a yoga mat is of dimensions 10 \times 10 and the hall is of dimensions 1 \times 1000, and you’ll see the problem.

  • Using an integer variable to store the sum of mats
    This causes overflow errors. Consider a case where there are 10^5 halls and each hall has dimensions 1000 \times 1000 and a mat has dimensions 1 \times 1. Clearly you can have 10^6 mats in each hall, and hence, 10^{11} overall. Simply too big for an int. Use long in Java or long long in C++. Python users need not worry :slight_smile:

  • Formula errors
    It is important to note that a/b * c/d is not the same as (a/b)*(c/d)

SOLUTIONS:

Setter's Solution (Kabir Kanha Arora) - Java 
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        long l = scanner.nextLong();
        long b = scanner.nextLong();
        int N = scanner.nextInt();

        long ans = 0;   // IMPORTANT: Note that int is not sufficient, so we use long here.
        for (int i = 0; i < N; ++i) {
            long L_i = scanner.nextLong();
            long B_i = scanner.nextLong();
            // The max yoga mats possible in each room is the max of both orientations.
            ans += Math.max((L_i / l) * (B_i / b), (L_i / b) * (B_i / l));      // The brackets need to be precise.
        }
        System.out.println(ans);
    }
}
Tester's Solution (Vaibhav Gautam) - C++ 
#include <bits/stdc++.h>
using namespace std;
using ll = long long int;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    ll l, b;
    cin >> l >> b;
    int n;
    cin >> n;
    ll ans = 0;
    for (int i = 0; i < n; ++i) {
        ll L, B;
        cin >> L >> B;
        ll pos1 = (L / l) * (B / b);
        ll pos2 = (L / b) * (B / l);
        ans += max(pos1, pos2);
    }
    cout << ans << '\n';
}
Tester's Solution (Vaibhav Gautam) - Python 
l,b=map(int,input().split())
N=int(input())
ans=0
for i in range(0,N):
    L,B=map(int,input().split())
    #Parallel to x-axis
    pos1=(L//l)*(B//b)
    #Parallel to y-axis
    pos2=(L//b)*(B//l)
    ans+=max(pos1,pos2)
print(ans)
1 Like