PROBLEM LINK:
Setter: Vikas Pandey
Tester: Rahul Dugar
Editorialist: Ishmeet Singh Saggu
DIFFICULTY:
Easy-Medium
PREREQUISITES:
DFS, Greedy and Bipartite Graph
PROBLEM:
In a red-blue tree , each vertex is either red or blue, and adjacent vertices always have different colors.
You are given a tree with N vertices. The nodes of the tree are colored in either red or blue. You can swap the color of any two adjacent nodes. You have to make the given tree into a red-blue tree in the minimum number of swaps or state that it is impossible.
QUICK EXPLANATION:
- As tree is a bipartite graph, so root the tree at node 1 and run a dfs to assign the parity(i.e. parity0 and parity1).
- Minimum number of swaps required to swap the color of any 2 nodes without changing the color of nodes present on the path between them is equal to the distance between these two nodes.
- There are 2 possible assignments.
- Try to assign red color to nodes with parity0.
- Try to assign red color to nodes with parity1.
- Let us solve when we try to assign red color to nodes with parity0.
- For a subtree of node X if all the nodes in the subtree have the proper color then it is optimal to not disturb it.
- We will focus on two types of nodes.
- Type1 - It is having a parity1 and red in color.
- Type2 - It is having a parity0 and is blue in color.
- Now we will run a dfs and for each node X we will maintain 2 parameters, excess and req.
- excess - It is the count of nodes with Type1 present in its subtree and not yet swapped color with the node of Type2. And as we move up the dfs we will add it to our answer, where excess of node X is equal to the sum of excess of its child nodes and +1 if type(X) == Type1.
- req - It is the count of nodes with Type2 present in its subtree and not yet swapped color with the node of Type2. And as we move up the dfs we will add it to our answer, req of node X is equal to the sum of req of its child nodes and +1 if type(X) == Type2.
- Note! node X can have either a non-zero excess or a non-zero req or both be zero. Suppose we get excess = 5 and req = 3 by using above step, it will be optimal to swap 3 nodes from excess to fill the 3 nodes of req and their cost of swaps we have already added to our answer as we moved up the dfs. So new excess = 2 and req = 0 of subtree of node X. We will add this updated excess and req to our answer when we move up the dfs.
- Think how to know if an assignment is possible of not
- Similarly, We will do it for the other case in which we try to assign red color to nodes with parity1 and if the assignment is possible then we will take the minimum of these two, else we will take the case which is possible. And if both the cases are not possible then the answer is impossible and we will print -1.
EXPLANATION:
A tree is a bipartite graph, let us refer to it’s 2 parities(or 2 disjoint sets) as parity0 and parity1. So first run a dfs to assign parity to the nodes. Now it can be formed to a red-blue tree by swapping nodes, given that the count of red nodes is equal to either to the count of nodes with parity0 or parity1(because in that case count of blue nodes will be equal to the other parity). Otherwise, the answer is impossible.
Also to make the problem simpler we will only focus on assigning red color nodes because if they are assigned correctly all the blue color nodes will automatically be assigned correctly.
We will take two cases :
- When we are trying to assign the red color to the nodes with parity0 if the count of red color nodes is equal to the count of nodes with parity0.
- When we are trying to assign the red color to the nodes with parity1 if the count of red color nodes is equal to the count of nodes with parity1.
In explanation, I will explain the first case as the second case can be done similarly. So let’s start.
One observation is that you can swap the color of any two nodes in the tree without changing the color of nodes that are present on the path between them. And the minimum number of swaps required to do this is equal to the distance between these 2 nodes. I will explain it with some example:-
Example 1. We want to swap the color of node 1 to node 3 without changing the color of the in-between nodes.
We can do so by swapping nodes 2 and 3 first and then node 1 and 2. Total No. of swaps = 2.
Example 2. We want to swap the color of node 1 to node 4.
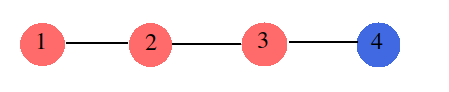
We can do so by swapping nodes 3 and 4 first, then node 2 and 3 and then node 1 and 2. Total No. of swaps = 3.
Example 3. We want to swap the color of node 1 to node 5.
We can do so by swapping nodes 3 and 4 first, then node 2 and 3, then node 1 and 2 and finally node 4 and 5. Total No. of swaps = 4.
By this observation, we can say that we can still change the color of other nodes without disturbing the nodes lying between the path. So it is optimal to not to disturb the nodes that have parity0 and red color or the node with parity1 and blue color as we can still freely swap the colors of the nodes.
- First, let us root the tree at node 1.
- For a subtree of node X if all the nodes in the subtree have the proper color then it is optimal to not disturb it.
Now consider two types of nodes :
- Type1 - It is having a parity1 and red in color.
- Type2 - It is having a parity0 and is blue in color.
Some Initial Thoughts
- Suppose we encounter a node with Type1 and it is either a leaf node or all it’s child subtrees are properly assigned. Then we have to pass it up the edge(joining this node and its parent) adding one to the answer. As the only option is to pass the red color up as all its child subtree is properly assigned.
- Similarly, if we encounter a node with Type2 and it is either a leaf node or all it’s child subtrees are properly assigned. Then it will require a red color, and its only option to get it through the edge joining it with the parent so it will also add one to our answer.
Now we will run a dfs and for each node X we will maintain 2 parameters, excess and req.
-
excess - It is the count of nodes with Type1 present in its subtree and not yet swapped color with the node of Type2. And as we move up the dfs (
exiting the dfs function of node X can be visualized as traveling up or traveling to its parent and is referred to as moving up the dfs) we will add it to our answer. As the only way is to send it above passing through the edge connecting node X and it’s parent, as all other nodes in the subtree of X are properly assigned. - req - It is the count of nodes with Type2 present in its subtree and not yet swapped color with with the node of Type1. And as we move up the dfs we will add it to our answer. As the only way is to get it from above passing through the edge connecting node X and it’s parent, as all other nodes in the subtree of X are properly assigned.
- excess of node X is equal to the sum of excess of its child nodes and +1 if its Type1.
excess[X] = 0;
if(type(X) == Type1) {
excess[X] ++;
}
for(auto child : graph[X]) {
if(child == parent) continue;
excess[X] += excess[child];
}
- req of node X is equal to the sum of req of its child nodes and +1 if its Type2.
req[X] = 0;
if(type(X) == Type2) {
req[X] ++;
}
for(auto child : graph[X]) {
if(child == parent) continue;
req[X] += req[child];
}
- Note! node X can have either a non-zero excess or a non-zero req or both be zero(in case the subtree is properly assigned). Why? because after computing excess and req for node X by using above steps suppose we get excess = 5 and req = 3, so instead of keeping it as same, what will be the optimal way to fulfill these requirements
, Yep we can swap 3 nodes from excess to fill the 3 nodes of req and there cost of swaps we have already added to our answer as we moved up the dfs. So new excess = 2 and req = 0 and this will be the excess and req of subtree of node X. So after computing excess and req we will update them as below and after that we will add it to our answer as we move up.
temp = min(excess[X], req[X]);
excess[X] -= temp;
req[X] -= temp;
- So if excess = req it means the subtree can be properly assigned by only using nodes in its own subtree as excess and req will become 0. So if excess = req for node 1(root) then we can consider the answer which we computed. Else it is not possible to make the red-blue tree in the current case(You can use this condition to reduce your implementation
).
Similarly, We will do it for the other case in which we try to assign red color to nodes with parity1 and if the assignment is possible then we will take the minimum of these two, else we will take the case which is possible. And if both the cases are not possible then the answer is impossible and we will print -1.
TIME COMPLEXITY:
- We are running one dfs to assign parity to the nodes and 2 dfs for both the cases of the assignment. So total time complexity per test case is O(N).
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define ff first
#define ss second
#define endl "\n"
vector<vector<int>> adj;
string s;
long long ans;
int dfs(int root, int par, int color)
{
int curr=0, c=s[root]-'0';
for(auto x:adj[root])
if(x!=par)
curr+=dfs(x, root, color^1);
if(c^color)
curr+=(c==0)?1:-1;
ans+=abs(curr);
return curr;
}
void solve()
{
long long n, fans=LLONG_MAX;
cin>>n;
adj.clear();
adj.resize(n);
for(int i=1; i<n; i++)
{
int u, v;
cin>>u>>v;
u--, v--;
adj[u].pb(v);
adj[v].pb(u);
}
cin>>s;
for(int rcolor=0, tmp=dfs(0, 0, rcolor); (rcolor<2); rcolor++, ans=0, tmp=dfs(0, 0, rcolor))
fans=tmp==0?min(fans, ans):fans;
cout<<((fans==LLONG_MAX)?-1:fans)<<endl;
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
cin>>t;
while(t--)
ans=0, solve();
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#ifndef rd
#define trace(...)
#define endl '\n'
#endif
#define pb push_back
#define fi first
#define se second
#define int long long
typedef long long ll;
typedef long double f80;
#define double long double
#define pii pair<int,int>
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int infi=0x3f3f3f3f;
//const int mod=998244353;
const int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
uniform_int_distribution<int> uid(0,lim-1);
return uid(rang);
}
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
vi gra[100005];
int dsu[100005];
int fpar(int u) {
return (dsu[u]<0)?u:dsu[u]=fpar(dsu[u]);
}
void merge(int u, int v) {
if((u=fpar(u))!=(v=fpar(v))) {
if(dsu[u]>dsu[v])
swap(u,v);
dsu[u]+=dsu[v];
dsu[v]=u;
}
}
int intend[100005],act[100005];
string s;
int dfs(int fr, int at, int bol) {
if(s[at-1]=='0')
act[at]++;
if(bol)
intend[at]++;
int res=0;
for(int i:gra[at]) {
if(i!=fr) {
res+=dfs(at,i,bol^1);
intend[at]+=intend[i];
act[at]+=act[i];
}
}
res+=abs(intend[at]-act[at]);
return res;
}
int sum_n=0;
void solve() {
int n=readIntLn(1,100000);
sum_n+=n;
memset(dsu,-1,sizeof(int)*(n+5));
fr(i,1,n)
gra[i].clear();
fr(i,2,n) {
int u=readIntSp(1,n),v=readIntLn(1,n);
assert(u!=v);
merge(u,v);
gra[u].pb(v);
gra[v].pb(u);
}
assert(dsu[fpar(1)]==-n);
s=readStringLn(n, n);
for(char i:s)
assert(i=='0'||i=='1');
int ans=infl;
memset(intend,0,sizeof(int)*(n+5));
memset(act,0,sizeof(int)*(n+5));
int temp=dfs(1,1,0);
if(intend[1]==act[1])
ans=min(ans,temp);
memset(intend,0,sizeof(int)*(n+5));
memset(act,0,sizeof(int)*(n+5));
temp=dfs(1,1,1);
if(intend[1]==act[1])
ans=min(ans,temp);
if(ans==infl)
ans=-1;
cout<<ans<<endl;
}
signed main() {
ios_base::sync_with_stdio(0),cin.tie(0);
srand(chrono::high_resolution_clock::now().time_since_epoch().count());
cout<<fixed<<setprecision(8);
int t=readIntLn(1,100);
while(t--)
solve();
assert(1<=sum_n&&sum_n<=1000000);
assert(getchar()==EOF);
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
const long long INF = 2e18;
int N;
long long ans;
vector<vector<int>> graph;
vector<int> parity, color, excess, req;
// below function assign parity to the node, NOTE, tree is a bipartite graph.
void assignParity(int node, int parent, int t) {
parity[node] = t;
for(auto to : graph[node]) {
if(to == parent) continue;
assignParity(to, node, t^1);
}
}
void dfs(int node, int parent, int prty) {
excess[node] = (parity[node] == prty);
req[node] = (color[node] == 0);
for(auto to : graph[node]) {
if(to == parent) continue;
dfs(to, node, prty);
excess[node] += excess[to];
req[node] += req[to];
}
int temp = min(excess[node], req[node]);
excess[node] -= temp;
req[node] -= temp;
ans += excess[node] + req[node]; // if the number of unsatisfied nodes is non-zero then it will contribute to our answer by swapping along the edge (node --- parent).
// exiting process of the dfs can be visualized as moving up an edge(node --- parent)
}
void solveTestCase() {
cin >> N;
graph.clear();
graph.resize(N+1);
parity.assign(N+1, 0);
color.assign(N+1, 0);
excess.assign(N+1, 0);
req.assign(N+1, 0);
for(int i = 0; i < N-1; i ++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for(int i = 1; i <= N; i ++) {
char in; cin >> in;
color[i] = (in-'0'); // let 0 be red color and 1 be blue color.
}
assignParity(1, -1, 0); // we will root the tree at node 1.
long long res = INF;
for(int i = 0; i < 2; i ++) {
ans = 0;
dfs(1, -1, i); // trying to assign color 0 to nodes with parity i, in minimum number of steps.
if(excess[1] == req[1]) { // If we have successfully assigned the nodes.
res = min(ans, res);
}
}
if(res == INF) cout << -1 << endl;
else cout << res << endl;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int testCase;
cin >> testCase;
for(int i = 1; i <= testCase; i ++) {
solveTestCase();
}
return 0;
}
Feel free to share your approach. In case of any doubt or anything is unclear please ask it in the comment section. Any suggestions are welcomed. 
) And my dfs function name is solve