PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Author: Sandeep V
Tester: Danny Mittal
Editorialist: Nishank Suresh
DIFFICULTY:
Easy
PREREQUISITES:
None
PROBLEM:
There is a square grid of size N\times N, where exactly N cells are blocked. Further, they are distributed such that there is exactly one blocked cell in every row and every column.
Is it possible to move from \left(1, 1\right) to \left(N, N\right) by taking only rightward and downward steps, without passing through any blocked cell?
QUICK EXPLANATION:
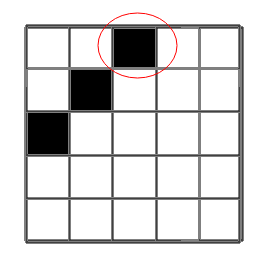
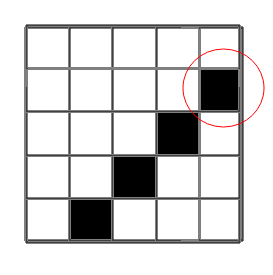
The answer is Yes if and only if no diagonal (with constant i+j) is filled with blocked cells.
EXPLANATION:
Drawing out a few examples on paper will likely give you the idea to check whether a diagonal is completely blocked.
This is both a necessary and a sufficient condition for a path to exist.
For convenience, the diagonal consisting of cells \left(i, j\right) such that i + j = c will be called diagonal c.
Proof of necessity
Suppose there is a path from \left(1, 1\right) to \left(N, N\right).
\left(1, 1\right) lies on diagonal 2, and each step we take, whether rightward or downward, moves us from diagonal i to diagonal i+1. As a result, we pass through exactly one square in each diagonal.
The only way such a path can exist is if every diagonal has at least one unblocked cell, making this a necessary condition.
Proof of sufficiency
Suppose that every diagonal has at least one unblocked cell. We will construct a path from \left(1, 1\right) to \left(N, N\right).
There is exactly one blocked cell in the first row - let it be \left(1, x\right) where x > 1. Let k be the smallest integer such that cells \left(1, x\right), \left(2, x-1\right), \dots, \left(k, x+1-k\right) are all blocked but cell \left(k+1, x-k\right) is not blocked.
This diagonal has at least one unblocked cell by assumption, so we know for a fact that k < x, i.e, x - k > 0.
Now do the following:
Move right from \left(1, 1\right) to \left(1, x-k\right). All these cells are not blocked because the only blocked cell in row 1 is in column x.
Then, move down to \left(k+1, x-k\right). Again, all these cells are unblocked because the cells blocked in rows 2, 3, \dots, k occur in columns after x-k, and \left(k+1, x-k\right) is unblocked by assumption.
Next, move right to \left(k+1, x\right). The cells along this path are unblocked because the blocked cells in each of these columns are above the path.
Finally, move down to \left(x, x\right).
We are now at position (x, x). Further, note that cells (x, x), (x+1, x), \dots, (N, x) are all unblocked because (1, x) is blocked.
We can now move from (x, x) to (N, N) via a similar constructive process.
The last row has exactly one blocked cell - let this be (N, y). Clearly, y = x is not possible.
- If y < x, we can simply move down to (N, x) and then right to (N, N), with all intermediate cells being unblocked.
- Suppose y > x. Let r be the smallest integer such that cells \left(N, y\right), \left(N-1, y+1\right), \dots, \left(N-r, y+r\right) are all blocked but cell \left(N-r-1, y+r+1\right) is not blocked.
Since all diagonals of the grid have an unblocked cell, such a r does exist, and will be < N-y.
Now do the following:
Move down to (N-r-1, x).
Next, move right to (N-r-1, y+r+1) - all intermediate cells are unblocked because the blocked cells in these columns are strictly below this path.
Next, move down to (N, y+r+1) - all intermediate cells are unblocked because the blocked cells in these rows are strictly to the left of this path.
Finally, move right to (N, N) and we are done.
All that remains is to check whether some diagonal is indeed blocked. A simple way to do this is to maintain a frequency table of x+y for every cell \left(x, y\right) in the input, and then iterate over every diagonal x+y and check whether freq[x+y] equals the length of that diagonal.
TIME COMPLEXITY:
\mathcal{O}(N\log N) or \mathcal{O}(N) per test.
CODE:
Setter (Python)
import sys
input=sys.stdin.readline
t=int(input())
for _ in range(t):
n=int(input())
c=dict()
for i in range(n):
a,b=map(int,input().split())
if(a+b in c):
c[a+b]+=1
else:
c[a+b]=1
fl=1
for i in range(2,n+1):
if(i in c):
if(c[i]==i-1):
fl=0
break
j=n+1
k=n
for i in range(n-1):
if(j in c):
if(c[j]==k):
fl=0
break
j+=1
k-=1
#print(j,k)
#print(c)
if(fl==0):
print("NO")
else:
print("YES")
Tester (Kotlin)
import java.io.BufferedInputStream
fun main(omkar: Array<String>) {
val jin = FastScanner()
repeat(jin.nextInt(1000)) {
val n = jin.nextInt(1000000)
val ys = IntArray(n + 1)
repeat(n) {
val x = jin.nextInt(n, false)
val y = jin.nextInt(n)
ys[x] = y
}
if (ys.toSet().size != n + 1) {
throw IllegalArgumentException("not all distinct y")
}
if ((1..n).any { ys[it] == 0 }) {
throw IllegalArgumentException("not all distinct x")
}
if (ys[1] == 1 || ys[n] == n) {
throw IllegalArgumentException("start and/or finish blocked")
}
println(if ((1..ys[1]).all { it + ys[it] == 1 + ys[1] } || (ys[n]..n).all { it + ys[it] == n + ys[n] }) "nO" else "yEs")
}
}
class FastScanner {
private val BS = 1 shl 16
private val NC = 0.toChar()
private val buf = ByteArray(BS)
private var bId = 0
private var size = 0
private var c = NC
private var `in`: BufferedInputStream? = null
constructor() {
`in` = BufferedInputStream(System.`in`, BS)
}
private val char: Char
private get() {
while (bId == size) {
size = try {
`in`!!.read(buf)
} catch (e: Exception) {
return NC
}
if (size == -1) return NC
bId = 0
}
return buf[bId++].toChar()
}
fun nextInt(): Int {
var neg = false
if (c == NC) c = char
while (c < '0' || c > '9') {
if (c == '-') neg = true
c = char
}
var res = 0
while (c >= '0' && c <= '9') {
res = (res shl 3) + (res shl 1) + (c - '0')
c = char
}
return if (neg) -res else res
}
fun nextInt(unused1: Int, unused2: Boolean = true) = nextInt()
fun nextInt(unused1: Int, unused2: Int, unused3: Boolean = true) = nextInt()
}
Editorialist (C++)
#include "bits/stdc++.h"
// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,mmx,avx,avx2")
using namespace std;
using ll = long long int;
mt19937_64 rng(chrono::high_resolution_clock::now().time_since_epoch().count());
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
int t; cin >> t;
while (t--) {
int n; cin >> n;
vector<array<int, 2>> v(n);
for (auto &[x, y] : v)
cin >> x >> y;
sort(begin(v), end(v));
int lst = 0;
for (int i = 1; i < n; ++i) {
if (v[i][1] == v[i-1][1] - 1) lst = i;
else break;
}
if (v[lst][1] == 1) {
cout << "No\n";
continue;
}
reverse(begin(v), end(v));
lst = 0;
for (int i = 1; i < n; ++i) {
if (v[i][1] == v[i-1][1] + 1) lst = i;
else break;
}
if (v[lst][1] == n) {
cout << "No\n";
continue;
}
cout << "Yes\n";
}
}