PROBLEM LINK:
Author: Ritesh Gupta
Tester: Sachin Yadav
Editorialist: Ritesh Gupta
DIFFICULTY:
EASY
PREREQUISITES:
MATH, EQUATIONS
PROBLEM:
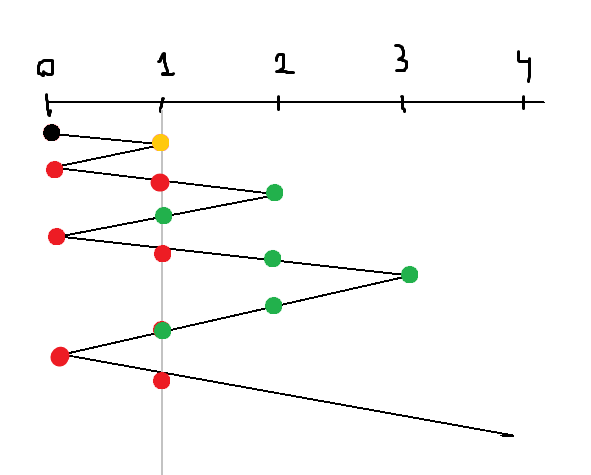
A game is defined on non-negative x-axis as you have to start your journey from 0_{th} location in positive x direction and every time you visit a new integer location, you have to come again at 0^{th} position. It will take 1 second to reach from i^{th} location to (i-1)^{th} location or (i+1)^{th} location**.
You are given two non-negative integers N(0 \le N \le 10^9) and K(1 \le K \le 10^9). You have to tell the time at which you arrive at x = N location on the positive x-axis for K^{th} time.
QUICK EXPLANATION:
- For 0^{th} location, the time at which you are here are: \{0,2,6,12...\} which is given by K * (K-1).
- For any other location, the answer is given by - N * N + (K//2) * (2*N) + ((K+1)//2) * ((K+1)//2 - 1) where // represents the integer division.
EXPLANATION:
-
For N = 0, we know that we will reach the 0^{th} location for every time we visit a new location. So, we observe that time taken to visit an i^{th} location from the 0^{th} location and come back to 0^{th} location, is equal to 2*i and if we formulate it then the K^{th} term is given by K * (K-1).
-
Otherwise, we know that we visit any i^{th} location first time after visiting 0^{th} location (i-1) times plus the time is taken from 0^{th} location to i^{th} location which takes (i-1)*(i) + i = i*i.
- The second time, it will take time equal to the first time + \space 2*i, as it will go up to 0^{th} location and come back again.
- The third time, it will take time equal to the second time + \space 2, as it will go up to (i+1)^{th} location and come back again.
- The fourth time, it will take time equal to the third time + \space 2*i, as it will go up to 0^{th} location and come back again.
- The fifth time, it will take time equal to the fourth time + \space 4, as it will go up to (i+2)^{th} location and come back again.
And so on…
By formulating, it evaluates to N * N + (K//2) * (2*N) + ((K+1)//2) * ((K+1)//2 - 1) where // represents the integer division, N(>0) is the location and K(>=0) is the count of the visit.
TIME COMPLEXITY:
TIME: O(1)
SPACE: O(1)
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
#define int long long
#define mod 1000000007
#define endl "\n"
using namespace std;
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
if(n == 0)
{
cout << (k*(k-1))%mod << endl;
continue;
}
int ans = n*n;
ans %= mod;
ans += 2*(k/2)*n;
ans %= mod;
k = (k+1)/2;
ans += k*(k-1);
ans %= mod;
cout << ans << endl;
}
}
Tester's Solution
T=int(input())
MOD=int(1e9+7)
for t in range(T):
N,K=[int(a) for a in input().split()]
M=K//2
# ans= ((K%2)?( (N+M)*(N+M) + M ):( (N+M)*(N+M) - M) )
ans=(N+M)*(N+M) -M
if(K%2):
ans+=2*M
if(N==0):
ans=K*(K-1)
print(ans%MOD)