How ?
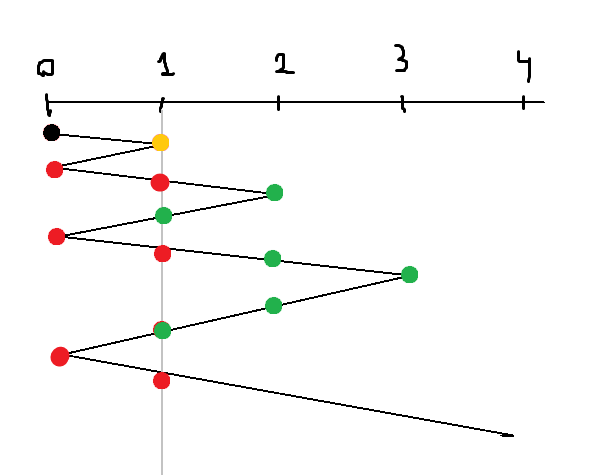
Consider case of n = 1 Till first occurance we have n^2 time elapsed (golden in image). Then onwards look at the points to the left and points to the right.
The left points (red) form mountains of constant height and each containing 2n points.
The right mountains (green) form a sequence 2, 4, 6, 8. Now all that remains is to find out how many of these left and right mountains are required to reach our k.
If you look at editorial expression, the first term is time to reach k = 1. Second term is contribution of left mountains, and third term is contribution of right mountains.
if k is even
(n+(k/2))(n+(k/2))-(k/2)
else
(n+(k/2))(n+(k/2))+(k/2)
See all sequences starting from 0 and ending to 1 as a block. We can get the index of 0 by the formula i*(i+1), where i is the index of the i’th occurence of 0 . Upto the i’th block, the total count of n is 1+(i-n)*2. At each stage, see if this is less than or greater than k and recurse.
General term of sequence where difference of numbers of sequence differ by 2 is pow(n,2)+ c*n +k where c and k can be calculated by plugging in some values of n (n denotes the term number of sequence).
Can anyone help me with this plz…which test case will not work with the following code??
ll n,k,x,ans;
cin>>n>>k;
if(n==0)
cout<<((k)*(k-1))%MOD<<endl;
else{
x = (n+k/2)%MOD;
ans = (x * x)%MOD;
if(k&1){
ans = (ans+abs(n-x))%MOD;
}
else{
ans -= abs(n-x);
}
cout<<ans<<endl;
It’s because of overflow 
Try this testcase 1000000000 1000000000
Thanks. But I’m still getting wrong submission with this changed code.
ll n,k,x;
unsigned ll ans;
cin>>n>>k;
if(n==0){
cout<<((k)*(k-1))%MOD<<endl;
}
else{
x = (n+k/2)%MOD;
ans = (x*x)%MOD;
if(k&1){
ans = (ans+abs(n-x))%MOD;
}
else{
ans = (ans-abs(n-x))%MOD;
}
cout<<ans<<endl;
}
Can u tell what I’m doing wrong.
I am not able to find what’s wrong with my code. Here’s my code
can please somebody help me…
#define lli long long int
#define mod 1000000007
#include
using namespace std;
#include<bits/stdc++.h>
inline lli read ()
{
char c;
lli n = 0;
while ((c = getchar_unlocked ()) < 48);
n += (c - ‘0’);
while ((c = getchar_unlocked ()) >= 48)
n = n * 10 + (c - ‘0’);
return n;
}
int main(void)
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
lli T=read();
while(T--)
{
lli n=read(),k=read();
// t=n*(n+1) this formula is for total time of nth round (returned back to zero)
lli t=((n%mod)*((n+1)%mod))%mod;
k--;
if(k>0)
{
/*
t=(n+(k/2))*(n+(k/2)+1) same as above but putting k/2 extra rounds with n
i.e. putting n=n+(k/2)
*/
t=(( ((n%mod) + ((k/2)%mod) )%mod) * ((((n%mod) + ((k/2)%mod) +1))%mod));
if(k%2==0)
t=((t%mod)-(n%mod))%mod;//t=t-n
else
t=((t%mod)+(n%mod))%mod;//t=t+n
}
else
t=( (t%mod)-(n%mod))%mod;//t=t-n
cout<<t%mod<<endl;
}
return 0;
}
instead of using long long for n, k. Can we use ‘int’ for them? And only use a long long variable to store the ans. Is this possible or will it overflow then?
Here is my Code for RECNDNUM. It passes all the sample test cases, then where it is going wrong…
I tried many random test case generators and compared my code with the Setter’s solution. Outputs are identical in all cases. I don’t know what’s wrong. Any one try and find a test case?
Desperate af T_T
heyy geek, please have look on my code.
I used the concept of sum of AP and the first time we find n is n*n
#include
#include
#include <bits/stdc++.h>
#include
using namespace std;
#define ll long long int
int mod=1e9+7;
ll fxp(ll a,ll b,ll m)
{
if(b==2)
return (aa)%m;
if(b%2==0)
return fxp(aa,b/2,m);
return fxp(a,b-1,m)*a;
}
void swap(ll &a,ll &b){ ll t=a; a=b; b=t;}
int main() {
// your code goes here
int t;
cin>>t;
while(t–)
{
ll n,k;
cin>>n>>k;
int res=0;
res=nn;
k=k-1;
if(n==0 && k>0)
{
if(k%2==0)
res+=(k/2)(4+(k-1)2);
else
res+=((k(4+(k-1)*2))/2);
}
else
if(k%2==0 && k!=0)
{
res+=(n*2)*k/2;
ll x=k/2;
res+=(x*(4+(x-1)*2))/2;
}
else if(k%2!=0 && k!=0)
{
res+=(n*2)*(k/2)+n*2;
ll x=k/2;
res+=(x/2)*(4+(x-1)*2);
}
cout<<(res%mod)<<endl;
}
return 0;
}
@rishup_nitdgp why this solution (in which I used long long) is giving wrong answer but in setter’s solution which used int ans = n * n which is not overflowing whereas in my solution even though I used long long and took modulo at every step then also it resulted in WA.
How come??
My same logic worked in pypy3 so my logic was correct and it was an overflow error then how come when n could be as large as 10^9 and your solution is working?
The ans may be negative when you subtract k/2.
Can anyone tell me which test case will not be executed with this code : -
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const long long MOD = (long long)(1e9 + 7);
ll solve(ll t)
{
ll n,k,start;cin>>n>>k;
if(n==0)
start=1;
else if(n>0)start=n;
if(k==1)cout<<(n*n)%MOD;
else
{k–;
while(k>0)
{start++;
k-=2;
start%=MOD;
if(k<=0)break;
}
if(k<0)
cout<<(((start-1)*start)+n)%MOD;
else
cout<<(((start-1)*start)+start+(start-n))%MOD;
}
if(t>0)cout<<"\n";
}
int32_t main()
{
#ifdef ONPC
freopen(“input.txt”, “r”, stdin);
#endif
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
ll t;cin>>t;while(t–)
{
solve(t);
}
return 0;
}
But it is working in pypy3.
The point is how the setter’s solution working even though it will definitely overflow for large values of n when ans = n^2.