PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: Ildar Gainullin
Tester: Nikolay Budin
Editorialist: Alei Reyes
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Eulerian Paths
PROBLEM:
There are m tiles in different cells of a n \times n chessboard.
Your goal is to start a rook in any of the given tiles and move it m-1 times (as it is a rook, you can only move it to any other cell on the same row or column), visiting all given tiles, and alternating the type of the used move (so you can’t move the rook to some cell in the same row two times in a row and you can’t move the rook to some cell in the same column two times in a row).
QUICK EXPLANATION:
Construct bipartite graph where Left represents the rows and Right the columns.
For each tile at cell (r,c), add an edge connecting vertex r from left to vertex c from right.
An eulerian path in such graph gives the order in which the cells can be visited.
EXPLANATION:
Finding a hamiltonian path in a general graph is NP-complete. Instead of thinking on how to go through all cells, sometimes is useful to find a graph where we have to go through all edges, which is a problem that can be solved in linear time (Eulerian Path ).
The structure of rows and columns in a chessboard can be represented very naturally by a bipartite graph.
Let’s construct an undirected bipartite graph G where Left represent the rows and Right the columns.
A tile at position (r,c) can be represented as an edge that connects r from Left to c from right.
If we follow a path in G, adjacent edges represent cells that can be reached by a rook because they share either a row or a column.
However a rook has two types of moves (horizontal and vertical), and we are interested in moving a rook from tile to tile by alternating the type of move.
It turns out that the bipartiteness of the graph also allows to model the two types of move. We can go through tile (r,c) by moving in the graph in two different ways:
- r \rightarrow c, it means we moved towards (r,c) using a horizontal move. After visiting the tile we have to move using a vertical move i.e to a different row using an edge c \rightarrow r'
- c \rightarrow r, it means we moved towards (r,c) using a vertical move. After visiting the tile we have to move using a horizontal move i.e to a different column using an edge r \rightarrow c'.
Therefore the problem is reduced to find a path that visits all edges of the graph exactly once i.e an eulerian path.
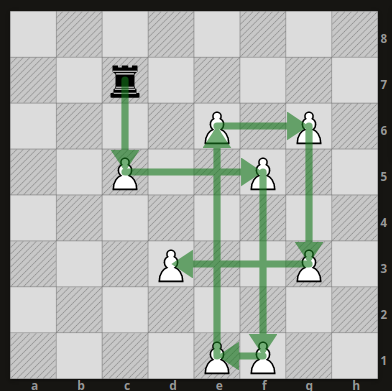
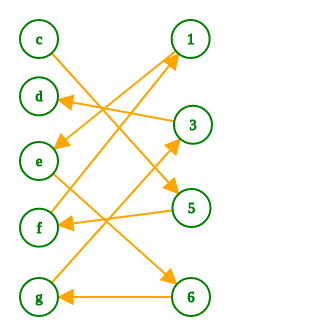
The following picture depicts the bipartite graph of the above board distribution. Each pawn represents a tile. If you start from node c and follow the arrows, you will walk through an eulerian path.
SOLUTIONS:
Setter's Solution
int main() {
int t;
cin >> t;
while (t--) {
int n, m;
cin >> n >> m;
vector <int> dsu(n + n);
vector <int> deg(n + n);
vector <int> empt(n + n);
for (int i= 0; i < n + n; i++) dsu[i] = i;
function<int(int)> get = [&] (int v) {
if (v == dsu[v]) return v;
else return dsu[v] = get(dsu[v]);
};
function<void(int,int)> uni = [&] (int u, int v) {
dsu[get(u)] = get(v);
};
vector <vector <pair <int, int> > > g(2 * n);
vector <char> used_e(m);
map <pair <int, int>, int> id;
for (int i = 0; i < m; i++) {
int r, c;
cin >> r >> c;
r--, c--;
empt[r]++, empt[n + c]++;
id[{r, n + c}] = i;
id[{n + c, r}] = i;
g[r].push_back({n + c, i});
g[n + c].push_back({r, i});
deg[r] ^= 1, deg[c + n] ^= 1;
uni(r, c + n);
}
bool bad = false;
int cnt = 0;
int start = 0;
set <int> ok;
for (int i = 0; i < n + n; i++) {
if (!empt[i]) continue;
ok.insert(get(i));
if (deg[i]) cnt++;
if (deg[i]) start = i;
}
if (bad || cnt > 2 || ok.size() > 1) assert(0);
else {
vector <int> ans;
function<void(int)> dfs = [&] (int v) {
while (!g[v].empty()) {
int i = g[v].back().second;
int to = g[v].back().first;
g[v].pop_back();
if (!used_e[i]) {
used_e[i] = true;
dfs(to);
}
}
ans.push_back(v);
};
dfs(start);
vector <int> p;
for (int i = 1; i < (int) ans.size(); i++) {
p.push_back(id[{ans[i - 1], ans[i]}]);
}
for (int i : p) {
cout << i + 1 << ' ';
}
cout << '\n';
}
}
}
Tester's Solution
void solve() {
int n, m;
cin >> n >> m;
map<pii, int> inds;
vector<vector<pii>> graph;
auto get_ind = [&](pii p) {
if (!inds.count(p)) {
int tmp = szof(inds);
inds[p] = tmp;
graph.push_back({});
}
return inds[p];
};
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
int a = get_ind({x, 1});
int b = get_ind({y, 2});
graph[a].push_back({b, i});
graph[b].push_back({a, i});
}
vector<int> odd;
for (int i = 0; i < szof(graph); ++i) {
if (szof(graph[i]) % 2) {
odd.push_back(i);
}
}
if (szof(odd) == 2) {
int a = odd[0];
int b = odd[1];
graph[a].push_back({b, m});
graph[b].push_back({a, m});
++m;
}
vector<bool> used(m);
vector<int> vcnt(szof(graph));
vector<int> cycle;
function<void(int)> dfs = [&](int v) {
while (vcnt[v] < szof(graph[v])) {
auto to = graph[v][vcnt[v]];
++vcnt[v];
if (!used[to.ss]) {
used[to.ss] = true;
dfs(to.ff);
cycle.push_back(to.ss);
}
}
};
dfs(0);
if (szof(odd) == 2) {
rotate(cycle.begin(), find(cycle.begin(), cycle.end(), m - 1), cycle.end());
cycle.erase(cycle.begin());
}
for (int ind : cycle) {
cout << ind + 1 << " ";
}
cout << "\n";
}