PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: Ildar Gainullin
Tester: Radoslav Dimitrov
Editorialist: Jelmer Firet
DIFFICULTY:
MEDIUM-HARD
PREREQUISITES:
Union Find datastructure
Kruskall’s algorithm for MST
PROBLEM:
You are given a graph G where vertex 1 is connected to all other vertices and G-\{1\} is connected. For each K from 1 to N-1 determine the minimum weight of a spanning tree where vertex 1 has degree K.
QUICK EXPLANATION:
Call G' the graph without vertex 1. Start with the spanning tree where we use all edges out of vertex 1. Step trough a modified Kruskal’s algorithm on G'. Each step we break a connection with 1 and replace it with an edge of G'. The modification of Kruskal’s algorithm ensures that the spanning trees we find have minimum weight.
EXPLANATION:
I will split this explanation in three parts: first I will reiterate the idea of Kruskal’s algorithm, then I will explain the idea of how we are going to use it and finally I explain how we need to modify Kruskal’s to make it work. Even if you are familiar with Kruskal’s algorithm I recommend to read the first section, as it gives a different view on Kruskal’s algorithm than the one you might know.
Kruskal’s algorithm
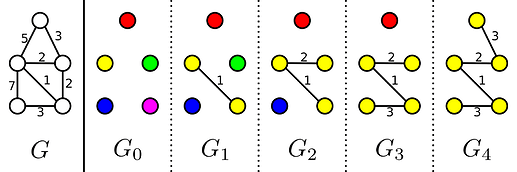
Kruskal’s algorithm is a greedy algorithm to solve the minimum spanning tree problem. It does so by evaluating all edges from shortest to longest, and we add an edge to the solution if it does not form a cycle with the existing edges. This can however be explained differently. If our graph has N vertices we start with a forest of N trees where each tree contains exactly one of the vertices. Then in each step of Kruskal’s algorithm we find the smallest edge joining two different trees, add it to the MST and merge those trees. In this sense Kruskal’s steps trough a sequence of N minimal-weight forests with k edges. I will label these k-edge forests with G_k. As you can see in the image below, the number of trees in G_k is equal to the number of vertices minus the number of edges.
That these intermediate forests have the smallest weight of all forests with k edges is not immediately obvious. I will give a proof below, but it is not necessary to understand for the rest of the explanation.
Proof
We first start with a lemma:
The largest edge in any k-edge forest is at least as big as the largest edge in G_k.
I am going to use proof by contradiction to show that this is the case. Assume that the graph H is also a k-edge forest but the largest edge is smaller than the largest edge in G_k. Then obviously there are some edges that differ between the two forests. Let’s call e the smallest weight edge in H but not in G_k. Note that e has weight smaller than the largest edge in G_k, so Kruskal’s algorithm evaluated it and concluded it would form a cycle with the included edges of smaller weight. Because f did not form a cycle in H there is at least one edge of this cycle not in H, call the smallest one of these f. Now S'=S-\{e\}+\{f\} also forms a k-edge forest. The largest edge of this forest did not increase, but it has one more edge matching with G_k. Repeating this procedure we can conclude that the largest edge of G_k is less than or equal to the largest edge of H. This gives a contradiction with the assumption, so the assumption must have been false and the lemma true.
Now using this lemma we can proof the minimality of G_k:
The weight of any k-edge forest is at least as big as the weight of G_k
We will proof this using induction and proof by contradiction.
For the induction basis we note that there is only one 0-edge forest, so G_0 has the smallest weight.
Now we assume (as the induction hypothesis) that we know that G_k is the smallest-weight k-edge forest. If we assume that G_{k+1} is not (for proof by contradiction) then there is a (k+1)-edge forest H bthat has smaller total weight than G_{k+1}. Then by our lemma we know that the largest edge of H is at least as big as the largest edge of G_{k+1}. If we remove the largest edge of H we end up with a k-edge forest H', and similarly removing the largest edge of $G_{k+1} gives us the k-edge forest G_k. But because H had smaller weight than G_{k+1} and the largest edge of H is at least as big as that of G_{k+1} it can only be the case that H' has smaller weight than G_k. However that would give a contradiction with our induction hypothesis, so G_{k+1} has the smallest weight finishing our induction.
Idea of the algorithm
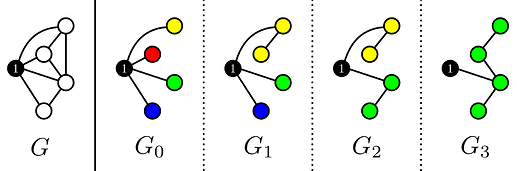
From the statement it is clear that we should handle vertex 1 differently from all other vertices. Therefore I will call the graph without vertex 1 and all it’s edges G'. Suppose that M is a spanning tree of G, then after removing vertex 1 we are left with a forest M'. The number of trees in M' is equal to the degree of vertex 1 in M. Using Kruskal’s on G' we can construct minimum weight forest’s with k edges (so the number of trees is |V|-k), and connect each tree with the smallest weight edge to vertex 1. The vertex of each tree that is connected to vertex 1 will be called the root of this tree.
Note that the solutions we find along the way have decreasing degree of vertex 1, so we need to output the total weights of these graphs in reverse order
This solution would not work out of the box however. Take a graph where a single edge from vertex 1 has really high weight. Then no matter the weights in G' we should select an edge to join so that we can remove the high weight edge to vertex 1 as soon as possible. Therefore we need to modify Kruskal’s algorithm to take into account the edges from vertex 1.
Modifying Kruskal’s algorithm
In a step (my definition) Kruskal’s algorithm would find the lowest weight edge and join the corresponding trees. However, the modified Kruskal’s algorithm should use the edge for which the total weight is increased the least if that edge is added and an edge from vertex 1 removed. Let’s call the increase in total weight the value of an edge. Then the value of an edge (u,v) is calculated as follows:
\text{value}(u,v) = \text{weight}(u,v) - \max(\text{weight}(1,\text{root(u)}), \text{weight}(1,\text{root(v)}))
This is because we add the edge (u,v) and break the largest of the two edges that now connect the new tree with vertex 1. This definition however introduces a new issue that we need to think about. The value of an edge doesn’t remain the same while executing Kruskal’s, so why does this produce correct results. We can find the answer by looking at the traditional explanation of Kruskal’s, namely that it evaluates the edges from smallest to largest and either discards or adds them to the minimum spanning tree. Whenever the modified Kruskal’s adds an edge to the MST, the value of edges can only increase. This means that edges that were not evaluated yet, remain larger than the one that’s being added. The order of the unevaluated edges only becomes important when an edge is evaluated, and by that time the value is set.
The implementation of this modified Kruskal’s is similar to the original. We use a heap (priority_queue) of edges to find the smallest unevaluated edge, and we use a Union Find data-structure to store which trees we currently have. The standard algorithm would then repeatedly do the following:
- fetch the smallest weight edge of the heap
- if it connects two different components → add it to the MST
- otherwise → discard it
The modified Kruskal’s instead uses the value of an edge as the key for the heap. In principle the edge values need to be updated every time two trees are joined, however this is hard without implementing our own heap. Instead we just continue until the edge emerges out of the heap, and then check if it needed to be updated. If it should have been updated we do so now and insert it back into the heap, otherwise we do Kruskal’s as normal. The only detail left is quickly finding the value an edge should have. For this we expand the Union Find data-structure to also store for each group the minimum weight of an edge from that group to vertex 1.
Small issue
I found a valid test case which would give my solution TLE. It is generated by the following code:
int N = 100000;
int M = 2*N-3;
cout << N << " " << M << endl;
for (int i = 2; i < N; i++) {
cout << 1 << " " << i << " " << 1 << endl;
}
for (int i = 1; i < N; i++) {
cout << i << " " << i+1 << " " << i+1 << endl;
}
Using an execution analysis tool (namely the callgrind tool of valgrind) I found out that almost 50% of the execution time was spend adding elements to the priority queue, and the other 50% removing elements from the priority queue. This was solved by pre-allocating the vector behind the priority_queue, instead of it making the container larger and smaller dynamically.
Complexity
As mentioned below, the complexity of this algorithm as explained is \mathcal{O}(VE\log E). Based on the comment of Radoslav (tester) this solution was still allowed to pass because a small modification would have made it \mathcal{O}(E\log E). I want to elaborate on his explanation of this trick a bit more.
The trick is to replace the single heap that stores all edges with multiple heaps, one global and multiple local ones for each component. The global heap contains the smallest edge out of each component heap. In the global heap the edges are sorted based on their value, as described above. The local heaps store all edges out of that component sorted on the edge’s weights.
In each step we extract the smallest edge from the global heap, which is guaranteed to be between two components. Suppose this edge joins u and v. We then merge the components of u and v, and so also their local heaps. Then look trough the edges in the merged local heap until you find the smallest-weight edge that goes to another component. Calculate the value of this edge and add it into the global heap.
Note that the C++ stdlib priority_queue does not implement an \mathcal{O}(\log n) merge of heaps, so we have to implement a heap that allows for fast merging ourselves.
ALTERNATE EXPLANATION:
Tester: Modified Kruskal’s
The approach the tester uses is similar to the one described above. There are however two changes between his solution and mine. First of all he uses set instead of priority_queue, though it has the same function. This did mean that he did not need to preallocate a vector to be used by the priority_queue. The second difference is in maintaining the shortest distance between vertex 1 and each component. Where I stored this information per component the tester instead made the root of each component the vertex with the smallest edge to vertex 1.
Setter: Dynamic Programming + Divide and Conquer + Heavy-Light Decomposition.
I will give a (relatively) short overview of the setter’s approach. I try to highlight all parts of his method, but to go into full detail would be enough for a second editorial. This means that sometimes I will be a bit handwavy/vague.
The setter used an entirely different approach. First he calculates the minimum spanning tree T of G', because only those edges of G' will be used in each of the spanning trees we are after. This minimum spanning tree is rooted at vertex 2. Then he uses dynamic programming over this tree to find the answer for all K. Call T_v the subtree in G' with highest vertex v. Then dp[v][1][k] gives the minimum weight of a spanning tree of the subgraph T_v+\{1\} that in which vertex 1 has k edges. dp[v][0][k] calculates the min. weight spanning forest with two trees, one containing v and the other containing 1, where vertex 1 has degree k. So the second coordinate encodes the number of connections from the component of vertex v to vertex 1.
The base cases of this dp table are relatively easy. Suppose v is a leaf, so has no children. Then dp[v][0][0]=0 and dp[v][0][k]=inf for k\neq 0. Furthermore dp[v][1][k]=inf for k\neq 1, dp[v][1][1]=weight(1,v). In the update we consider each of the children one by one.
Suppose u is the parent and v is the child. To join the components of u and v there are multiple factors we need to account for:
- whether the component of u is/isn’t connected to vertex 1
- whether the component of v is/isn’t connected to vertex 1
- whether we want to use the edge (u,v) or not.
Of the 8 total combinations 5 remain valid (no two connections to 1 from a single component, only the component containing u may remain disconnected from 1). For each of these combinations we “merge” dp[u][i] and dp[v][j] and use that to update dp[u][k] (relax). The merge takes two arrays a and b and makes an array c such that c[k]=\min\{a[i]+b[j]|i+j=k\}, and does this in \mathcal{O}(|a|+|b|) by looking at the differences between adjacent cells.
This algorithm would be \mathcal{O}(n^2) which is too slow, so we need to use some tricks to speed it up. We need to make sure that each time we merge the arrays that are being merged are as small as possible.
The first optimization to achieve this is to use divide and conquer for merging the children of each vertex. We perform multiple rounds of merging. In the first round we merge child 1 and 2, child 3 and 4, child 5 and 6, … . In the next round we merge {1,2} and {3,4}, {5,6} and {7,8}, … . This way we perform \log c rounds where in each round we only merge each element once. This is done in the function dfs
The second optimization is to use heavy-light decomposition on T, and only perform the above described joining for the light edges. The subtree of the lower vertex in a light edge has at most half the vertices as the subtree of the parent, so with the D&C approach of the previous paragraph the complexity for all light edge joins becomes $\mathcal{O}(n\log n). The heavy edges form paths in T, on which we will perform a more difficult operation to merge all vertices in a heavy path (still D&C with total complexity \mathcal{O}(n\log n), also needs to consider whether the bottom component is connected to vertex 1 or not and whether the entire path is in one component or not). This is done in the function restore.
In the end the algorithm of the setter is \mathcal{O}(n\log n) but much more complex than the modified Kruskal’s algorithm.
SOLUTIONS:
Setter's Solution
#include <cmath>
#include <functional>
#include <fstream>
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <map>
#include <list>
#include <time.h>
#include <math.h>
#include <random>
#include <deque>
#include <queue>
#include <cassert>
#include <unordered_map>
#include <unordered_set>
#include <iomanip>
#include <bitset>
#include <sstream>
#include <chrono>
#include <cstring>
using namespace std;
typedef long long ll;
#ifdef iq
mt19937 rnd(228);
#else
mt19937 rnd(chrono::high_resolution_clock::now().time_since_epoch().count());
#endif
const int N = 2e5;
const ll inf = (ll) (1e18) + 7;
int dsu[N];
int get(int v) {
if (v == dsu[v])
return v;
else
return dsu[v] = get(dsu[v]);
}
void uni(int u, int v) {
dsu[get(u)] = get(v);
}
vector <pair <int, int> > adjList[N];
vector <ll> dp[N][2];
int in[N];
void convex(vector <ll> a) {
while (!a.empty() && a.back() == inf) a.pop_back();
for (int i = 2; i < (int) a.size(); i++) {
assert(a[i] - a[i - 1] >= a[i - 1] - a[i - 2]);
}
}
vector <ll> merge(vector <ll> a, vector <ll> b, ll w) {
while (!a.empty() && a.back() == inf) a.pop_back();
while (!b.empty() && b.back() == inf) b.pop_back();
if (a.empty() || b.empty()) return {};
int p = 0, q = 0;
while (a[p] == inf) p++;
while (b[q] == inf) q++;
vector <ll> cur;
for (int i = 0; i < p + q; i++) cur.push_back(inf);
cur.push_back(a[p] + b[q] + w);
vector <ll> ders_a;
for (int i = p + 1; i < (int) a.size(); i++) {
ders_a.push_back(a[i] - a[i - 1]);
}
vector <ll> ders_b;
for (int i = q + 1; i < (int) b.size(); i++) {
ders_b.push_back(b[i] - b[i - 1]);
}
vector <ll> ders(ders_a.size() + ders_b.size());
merge(ders_a.begin(), ders_a.end(), ders_b.begin(), ders_b.end(), ders.begin());
for (ll x : ders) {
cur.push_back(cur.back() + x);
}
return cur;
}
void relax(vector <ll> &a, vector <ll> b) {
while (a.size() < b.size()) a.push_back(inf);
for (int i = 0; i < (int) b.size(); i++) {
a[i] = min(a[i], b[i]);
}
}
int sz[N];
pair <int, int> jump[N];
vector <ll> same[4 * N][2];
vector <ll> ret[4 * N][2][2];
void restore(int x) {
int root = x;
vector <int> ord;
vector <int> ws;
while (true) {
ord.push_back(x);
if (jump[x].second == -1) break;
ws.push_back(jump[x].second);
x = jump[x].first;
}
function<void(int,int,int)> solve = [&] (int v, int l, int r) {
for (int i = 0; i < 2; i++) for (int j = 0; j < 2; j++) ret[v][i][j].clear();
for (int i = 0; i < 2; i++) same[v][i].clear();
if (r - l == 1) {
same[v][0] = dp[ord[l]][0];
same[v][1] = dp[ord[l]][1];
} else {
int m = (l + r) / 2;
ll w = ws[m - 1];
solve(v * 2 + 1, l, m);
solve(v * 2 + 2, m, r);
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
if (i + j < 2)
relax(same[v][i + j], merge(same[v * 2 + 1][i], same[v * 2 + 2][j], w));
relax(ret[v][i][j], merge(same[v * 2 + 1][i], same[v * 2 + 2][j], 0ll));
}
}
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
if (j == 1) {
relax(ret[v][i][k], merge(same[v * 2 + 1][i], ret[v * 2 + 2][j][k], 0ll));
relax(ret[v][k][i], merge(ret[v * 2 + 1][k][j], same[v * 2 + 2][i], 0ll));
}
if (i + j < 2) {
relax(ret[v][i + j][k], merge(same[v * 2 + 1][i], ret[v * 2 + 2][j][k], w));
relax(ret[v][k][i + j], merge(ret[v * 2 + 1][k][j], same[v * 2 + 2][i], w));
}
}
}
}
for (int i = 0; i < 2; i++) {
relax(ret[v * 2 + 1][i][i], same[v * 2 + 1][i]);
relax(ret[v * 2 + 2][i][i], same[v * 2 + 2][i]);
}
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
for (int t = 0; t < 2; t++) {
if (j + k == 1)
relax(ret[v][i][t], merge(ret[v * 2 + 1][i][j], ret[v * 2 + 2][k][t], w));
if (j == 1 && k == 1) {
relax(ret[v][i][t], merge(ret[v * 2 + 1][i][j], ret[v * 2 + 2][k][t], 0ll));
}
}
}
}
}
}
};
solve(0, 0, (int) ord.size());
dp[root][0].clear(), dp[root][1].clear();
relax(dp[root][0], ret[0][0][1]);
relax(dp[root][0], same[0][0]);
relax(dp[root][1], ret[0][1][1]);
relax(dp[root][1], same[0][1]);
}
void dfs(int cur, int prev) {
dp[cur][0] = {0};
dp[cur][1] = {inf, in[cur]};
sz[cur] = 1;
vector <pair <int, pair <int, int> > > ch;
for (auto c : adjList[cur]) {
int to = c.first;
int w = c.second;
if (to != prev) {
dfs(to, cur);
sz[cur] += sz[to];
ch.push_back({sz[to], {to, w}});
}
}
sort(ch.rbegin(), ch.rend());
int large = -1;
jump[cur] = make_pair(-1, -1);
if (!ch.empty()) {
large = ch[0].second.first;
jump[cur] = make_pair(large, ch[0].second.second);
ch.erase(ch.begin());
}
vector <vector <vector <ll> > > s;
for (auto c : ch) {
int to = c.second.first;
restore(to);
int w = c.second.second;
vector <vector <ll> > go(2);
relax(go[0], merge(dp[cur][0], dp[to][0], w));
relax(go[0], merge(dp[cur][0], dp[to][1], 0ll));
relax(go[1], merge(dp[cur][0], dp[to][1], w));
/*
cout << "0" << endl;
convex(go[0]);
cout << "1" << endl;
convex(go[1]);
cout << "2" << endl;
*/
//relax(go[1], merge(dp[cur][1], dp[to][0], w));
//relax(go[1], merge(dp[cur][1], dp[to][1], 0ll));
s.push_back(go);
}
s.push_back({dp[cur][0], dp[cur][1]});
function<vector<vector<ll> >(int, int)> solve = [&] (int l, int r) {
if (r - l == 1) {
return s[l];
} else {
int m = (l + r) / 2;
auto a = solve(l, m);
auto b = solve(m, r);
vector <vector <ll> > go(2);
for (int i = 0; i < 2; i++) {
for (int j = 0; i + j < 2; j++) {
relax(go[i + j], merge(a[i], b[j], 0ll));
}
}
return go;
}
};
auto p = solve(0, (int) s.size());
dp[cur][0] = p[0], dp[cur][1] = p[1];
/*
cout << "3" << endl;
convex(dp[cur][0]);
cout << "4" << endl;
for (ll p : dp[cur][1]) cout << p << ' ';
cout << endl;
convex(dp[cur][1]);
cout << "5" << endl;
*/
/*
for (int i = 0; i < (int) dp[cur][0].size(); i++) {
for (int j = 0; j < (int) dp[to][0].size(); j++) {
go[0][i + j] = min(go[0][i + j], dp[cur][0][i] + dp[to][0][j] + w);
}
}
for (int i = 0; i < (int) dp[cur][0].size(); i++) {
for (int j = 0; j < (int) dp[to][1].size(); j++) {
go[0][i + j] = min(go[0][i + j], dp[cur][0][i] + dp[to][1][j]);
go[1][i + j] = min(go[1][i + j], dp[cur][0][i] + dp[to][1][j] + w);
}
}
for (int i = 0; i < (int) dp[cur][1].size(); i++) {
for (int j = 0; j < (int) dp[to][0].size(); j++) {
go[1][i + j] = min(go[1][i + j], dp[cur][1][i] + dp[to][0][j] + w);
}
}
for (int i = 0; i < (int) dp[cur][1].size(); i++) {
for (int j = 0; j < (int) dp[to][1].size(); j++) {
go[1][i + j] = min(go[1][i + j], dp[cur][1][i] + dp[to][1][j]);
}
}
*/
/*
convex(dp[cur][1]);
convex(dp[cur][0]);
*/
}
int main() {
#ifdef iq
freopen("a.in", "r", stdin);
#endif
ios::sync_with_stdio(0);
cin.tie(0);
{
int n, m;
for (int i = 0; i < n; i++) adjList[i].clear();
cin >> n >> m;
vector <pair <int, pair <int, int> > > edgeList;
/*
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int w = rnd() % 1000 + 1;
if (i == 0) in[j] = w;
else edgeList.push_back({w, {i, j}});
}
}
*/
for (int i = 0; i < m; i++) {
int u, v, w;
cin >> u >> v >> w;
u--, v--;
if (u == 0) {
in[v] = w;
} else {
edgeList.push_back({w, {u, v}});
}
}
sort(edgeList.begin(), edgeList.end());
for (int i = 0; i < n; i++) dsu[i] = i;
for (auto c : edgeList) {
int u = c.second.first, v = c.second.second;
int w = c.first;
if (get(u) != get(v)) {
uni(u, v);
adjList[u].push_back({v, w});
adjList[v].push_back({u, w});
}
}
dfs(1, -1);
restore(1);
for (int i = 1; i <= n - 1; i++) {
assert(i < (int) dp[1][1].size());
cout << dp[1][1][i] << ' ';
}
cout << endl;
}
}
Tester's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (1 << 20);
struct edge {
int u, v, w;
edge() { u = v = w = 0; }
edge(int _u, int _v, int _w) {
u = _u;
v = _v;
w = _w;
}
};
edge e[MAXN];
int n, m;
int64_t sum;
int val[MAXN];
set<pair<int, pair<int, int> > > edge_values;
int par[MAXN];
int root(int x) {
return par[x] == x ? x : (par[x] = root(par[x]));
}
void read() {
sum = 0;
cin >> n >> m;
for(int i = 1; i <= n; i++) {
par[i] = i;
}
for(int i = 0; i < m; i++) {
int u, v, w;
cin >> u >> v >> w;
e[i] = edge(u, v, w);
if(u == 1) {
sum += w;
val[v] = w;
}
}
}
bool used[MAXN];
int64_t answer[MAXN];
void solve() {
for(int i = 0; i < m; i++) {
if(e[i].u != 1) {
edge_values.insert({e[i].w - val[e[i].u], {i, e[i].u}});
edge_values.insert({e[i].w - val[e[i].v], {i, e[i].v}});
}
}
answer[n - 1] = sum;
for(int i = n - 2; i >= 1; i--) {
while(true) {
auto it = edge_values.begin();
int w = it->first, i = it->second.first, v = it->second.second;
edge_values.erase(it);
if(used[i]) {
continue;
}
if(root(v) != v) {
edge_values.insert({e[i].w - val[root(v)], {i, root(v)}});
continue;
}
if(root(e[i].u) == root(e[i].v)) {
continue;
}
int u = root(e[i].u) == v ? root(e[i].v) : root(e[i].u);
sum += w;
par[v] = u;
used[i] = true;
break;
}
answer[i] = sum;
}
for(int i = 1; i <= n - 1; i++) {
cout << answer[i] << " ";
}
cout << endl;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
read();
solve();
return 0;
}
Editorialist's Solution
#include <iostream>
#include <vector>
#include <utility>
#include <tuple>
#include <algorithm>
#include <queue>
using namespace std;
typedef int64_t ll;
typedef vector<ll> vi;
struct edge{
int from, to;
ll weight;
friend bool operator<(const edge& lhs, const edge& rhs) {
return tie(lhs.from,lhs.to,lhs.weight) <
tie(rhs.from,rhs.to,rhs.weight);
}
};
typedef pair<ll,edge> update;
class UFDS
{
private:
vi parent,size,dist;
public:
UFDS(vi newDist) {
int newSize = newDist.size();
dist = newDist;
parent.resize(newSize);
for (int i = 0; i < newSize; i++) {
parent[i] = i;
}
size.assign(newSize,1);
}
int find(int x) {
if (x == parent[x]) {
return x;
}
parent[x] = find(parent[x]);
return parent[x];
}
bool same(int x, int y) {
return find(x) == find(y);
}
void join(int x, int y) {
x = find(x);
y = find(y);
if (x == y) return;
if (size[x] < size[y]) swap(x,y);
parent[y] = x;
size[x] += size[y];
dist[x] = dist[y] = min(dist[x],dist[y]);
}
int getDist(int x) {
return dist[find(x)];
}
};
int main() {
int numNode, numEdge;
cin >> numNode >> numEdge;
vector<edge> edgeList;
vi dist(numNode,0);
ll total = 0;
for (int i = 0; i < numEdge; i++) {
int from,to;
ll weight;
cin >> from >> to >> weight;
from--; to--;
if (from == 0) {
dist[to] = weight;
total += weight;
} else {
edgeList.push_back({from,to,weight});
}
}
UFDS conn(dist);
vector<update> updateContainer;
updateContainer.reserve(numEdge);
priority_queue<update,vector<update>,greater<update>> todo (greater<update>(), updateContainer);
for (edge edge : edgeList) {
ll value = edge.weight - max(conn.getDist(edge.from),conn.getDist(edge.to));
todo.push({value, edge});
}
vi result(numNode);
int degree = numNode-1;
result[degree--] = total;
while (not todo.empty()) {
ll value;
edge edge;
tie(value, edge) = todo.top();
todo.pop();
if (conn.same(edge.from,edge.to)) continue;
if (value != edge.weight - max(conn.getDist(edge.from), conn.getDist(edge.to))) {
value = edge.weight - max(conn.getDist(edge.from), conn.getDist(edge.to));
todo.push({value,edge});
continue;
}
total += value;
result[degree--] = total;
conn.join(edge.from,edge.to);
}
for (int deg = 1; deg < numNode; deg++) {
if (deg > 1) cout << " ";
cout << result[deg];
}
cout << endl;
return 0;
}