SAFETR - Editorial

psychik · August 23, 2020, 1:32pm

PROBLEM LINK:

Practice
Contest
Video Editorial

Setter: Arthur Nascimento
Tester: Rahul Dugar
Editorialist: Ishmeet Singh Saggu

DIFFICULTY:

Medium-Hard

PREREQUISITES:

Segment Tree/Fenwick Tree, Cummalative Sum Techniques, DFS and Maths

PROBLEM:

You have given a tree with N nodes. There are K special nodes called police stations which are situated at nodes V_1, V_2, \ldots, V_K, each special node has some radius of efficiency R_i. The ith police station increases the security level of node X by max(0, R_i-distance(X, V_i)). Initially, the security level of each node is 0. For each node, you have to compute the final security level of the node after considering the effect of each police station on it. Also for any station, it is observed that S_{V_i} = R_i, where S_X is the final security level of X.

QUICK EXPLANATION:

For any 2 stations V_i and V_j the distance between them is > max(R_i, R_j).
From the above observation, you will observe the condition R_1+ R_2+ \dots+ R_K \leq 2*N to be true.
Root the tree at node 1
Observe what will happen when you increase the security level of the nodes with val+d and subtracted the corresponding depths for the subtree of station X, where val is the radius of station X and d is its depth.
It is mentioned that for each station we will increase the security level of other nodes by max(0, R_i-distance(X, V_i)). So what can we do if depth[X] > depth[station]+R_i. so to handle this properly we need only those values whose magnitude is \geq depth[X]. To compute their sum we can maintain a data structure(Segment Tree or Fenwick Tree) which stores all the updates which are done on the ancestors of this node X including itself and provide the range sum of the values which is \geq depth[X]. Also, note suppose you do 2 operation of above types which are valid for node X(i.e. magnitude of their value is \geq depth[X]) so in that case, you have to subtract the depth[X] of the node 2 times from there sum. So we have to maintain another data structure(Segment Tree or Fenwick Tree) which stores all the updates which are done on the ancestors of this node X including itself and provide the range sum of the count of values which is \geq depth[X].

   ans[X] = sum_of_values_greater_than_depth[X] - (depth[X] * count_of_values_greater_than_depth[X])

Let us represent an update as (X, depth[X]+R, count) where the update is applied to the node X and value to be added is (depth[X]+R) and it is added count times.
To compute the answer for node X you will need only the update of the station which is either ancestor of X or X itself. So we will maintain only 2 data structure for all the nodes and as we move down the DFS we will perform all the updates associated with node X, (X, value+depth[station], count) to introduce its effect to nodes in its subtree, and when we move up we will perform the update as (X,value+depth[station], -count) to negate its effect.
To update the nodes for the security increase for station X, outside of its subtree you can do the following operation.
- To update the nodes of the subtree of station X for the effect of station X we can add an update to node X as
  (X, depth[x]+R, 1).
- To update the nodes of the subtree of Par[X] for the effect of station X we can add an update to node Par[X] as (Par[X], depth[Par[X]]+R-1, 1) and as we don’t want to effect subtree of X with this update we add an update to node X to negate its effect as (X, depth[Par[X]]+R-2, -1) (note the count is -1). Then we will assign X = Par[X] and R = R-1, and continue the process until R > 1 and there is some parent of current X.

EXPLANATION:

If you observe the line “She already finished her job and noticed an interesting coincidence: for each valid i, S_{V_i}=R_i” where S_X represents the security level of node X. You can deduce that for any 2 stations V_i and V_j the distance between them is > max(R_i, R_j). If you try to exploit this condition a little bit more you will observe the condition R_1+ R_2+ \dots+ R_K \leq 2*N to be true.

Proof

Let for each station i, we paint all the nodes X with color i which follow the condition dist(V_i,X) \leq \frac{R_i}{2}
let us consider a node u which is colored with A by station V_A and B by station V_B.
So it will implies that,
dist(V_A,V_B) \leq dist(V_A,u) + dist(u,V_b) \leq \frac{(R_A+R_B)}{2} \leq max(R_A,R_B)
which is a contradiction(As I have already mentioned distance between them is > max(R_i, R_j)).
So no node is present at the distance of \leq \frac{R_i}{2} of 2 stations which proves our condition.

Now let us see how we can exploit this condition to solve our problem.

Let us first root the tree at node 1 so we can introduce a parent-child-subtree relation in the tree.
Suppose we have a way to increase the value of subtree of node X by val. Now observe what will happen to the values of the node if we subtract it by there corresponding depths.
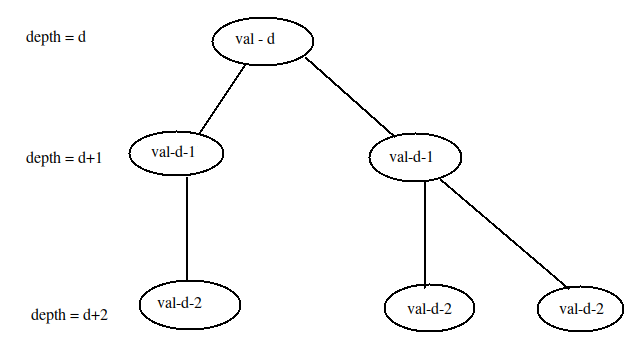
an_image_sub1_png
Now, what if instead of updating the value of subtree of node X by val, we have updated it with val+d, where d is the depth of node X and subtracted the corresponding depths.
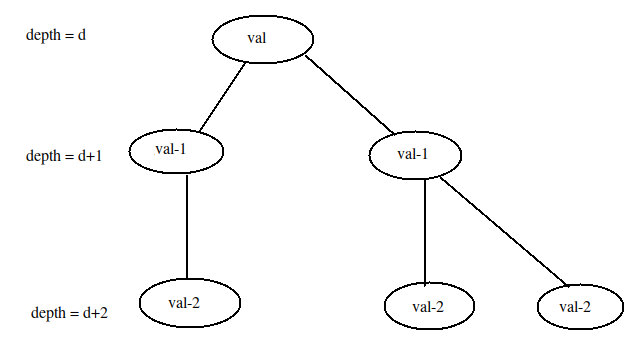
an_image_sub2_png
Doesn’t it seem similar to the update we are trying to do in the problem if X is considered as a station and val as R_i?

Now there are some conditions to note before applying the above operation.

It is mentioned that for each station we will increase the security level of other nodes by max(0, R_i-distance(X, V_i)). So what can we do if depth[X] > depth[station]+R_i. so to handle this properly we need only those values whose magnitude is \geq depth[X]. To compute their sum we can maintain a data structure(Segment Tree or Fenwick Tree) which stores all the updates which are done on the ancestors of this node X including itself and provide the range sum of the values which is \geq depth[X]. Also, note suppose you do 2 operation of above types which are valid for node X(i.e. magnitude of their value is \geq depth[X]) so in that case, you have to subtract the depth[X] of the node 2 times from there sum. So we have to maintain another data structure(Segment Tree or Fenwick Tree) which stores all the updates which are done on the ancestors of this node X including itself and provide the range sum of the count of values which is \geq depth[X].
So the final formula for a node X to compute its value is
```
 ans[X] = sum_of_values_greater_than_depth[X] - (depth[X] * count_of_values_greater_than_depth[X])
```
So each update can be represented as (X, value+depth[station], count) where the count is the number of times the (value+depth[station]) is added and X for whose subtree we are applying this update. So for station this update will look like (V_i, R_i+depth[V_i], 1)
Another difficulty which it posses is how to maintain 2 data structures for each node and how to update them,
For this, you will note that to compute the answer for node X you will need only the update of the station which is either ancestor of X or X itself. So we will maintain only 2 data structure for all the nodes and as we move down the DFS we will perform all the updates associated with node X, (X, value+depth[station], count) to introduce its effect to nodes in its subtree, and when we move up we will perform the update as (X,value+depth[station], -count) to negate its effect as the answer for all the nodes in its subtree is computed.

for(auto i : updates[node]) { // adding the effect of updates for the node, as it will effect the nodes in its subtree.
	long long value = depth[node] + i.first;
	long long count = i.second; 
	sum_depths.update(value, count*value); // as this value will impact only those nodes which have depths < value.
	count_depths.update(value, count);
}

for(auto i : updates[node]) { // removing the effect of updates for the node, as answer for all nodes in it's subtree is computed.
	long long value = depth[node] + i.first;
	long long count = -i.second; 
	sum_depths.update(value, count*value); // as this value will impact only those nodes which have depths < value.
	count_depths.update(value, count);
}

Now you might be wondering that updating subtree is ok, what about nodes outside the subtree of station V_i having radius R_i. As its parent should be increased by R_i-1 and so on(you can see the figure). The black node represents node X and its subtree and Red nodes represent nodes outside the subtree of X.

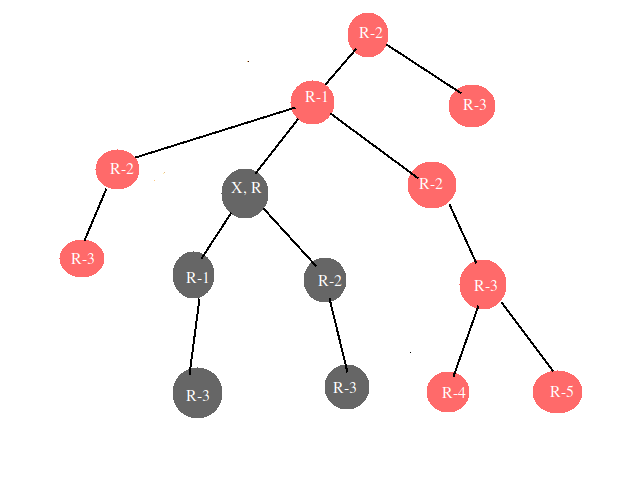
Note you update these nodes as follow
- To update the nodes of the subtree of station X for the effect of station X we can add an update to node X as
  (X, depth[x]+R, 1).
- To update the nodes of the subtree of Par[X] for the effect of station X we can add an update to node Par[X] as (Par[X], depth[Par[X]]+R-1, 1) and as we don’t want to effect subtree of X with this update we add an update to node X to negate its effect as (X, depth[Par[X]]+R-2, -1) (note the count is -1). Then we will assign X = Par[X] and R = R-1, and continue the process until R > 1 and there is some parent of current X.
- You might think why it will not get TLE because here we exploit the condition we proved above i.e. R_1+ R_2+ \dots+ R_K \leq 2*N.

updates[station].push_back({radious, 1}); // as we add values to its subtree.
while((parent[station] != -1) && (radious > 1)) { 
	radious --; // as its parent is at distance 1 from its child
	updates[parent[station]].push_back({radious, 1}); // as we add values to subtree of parent[station].
	if(radious > 1) { // but we don't want to add the values to subtree of station again as we have already added so to negate the effect of parent flag
		updates[station].push_back({radious-1, -1});
	}
	station = parent[station];
}

So by performing the update as we go down and negating the update of node X as we move up the DFS and by applying the formula, we can compute the answer.

TIME COMPLEXITY:

For each node X we are doing O(\log{N}) operation to compute the answer. So total time to compute the answer for all nodes will be O(N*\log{N}).
Also we are doing several updates in O(\log{N}). The total number of updates are in order of O(N). So total time to perform an update is O(N*\log{N}).
So total time complexity per test case is O(N*\log{N}).

SOLUTIONS:

Setter's Solution

#include <bits/stdc++.h>
#define ll long long
#define pb push_back
#define pii pair<int,int>
#define maxn 800800
#define mod 1000000007
#define debug 
using namespace std;

int n;
vector<int> L[maxn];
int par[maxn];
int mrk[maxn];
int rad[maxn];
int ans[maxn];

vector<pii> op[maxn];

int T[2][2*maxn];

void upd(int id,int idx,int val){
	idx++;
	while(idx <= 2*n+2){
		T[id][idx] += val;
		idx += (idx&-idx);
	}
}

int qry(int id,int idx){
	int r = 0;
	idx++;
	while(idx){
		r += T[id][idx];
		idx -= (idx&-idx);
	}
	return r;
}

#define Q(a,b) (qry(a,2*n+1)-qry(a,b-1))

void calc(int vx,int d=0){
	for(pii i : op[vx]){
		int x = d + i.first;
		upd(0,x,-i.second);
		upd(1,x,x*i.second);
	}
	ans[vx] = d * Q(0,d) + Q(1,d);
	for(int i : L[vx])
		if(i != par[vx])
			calc(i,d+1);
	for(pii i : op[vx]){
		int x = d + i.first;
		upd(0,x,i.second);
		upd(1,x,-x*i.second);
	}
}

void dfs(int vx){

	for(int i : L[vx])
		if(i != par[vx]){
			par[i] = vx;
			dfs(i);
		}

	if(mrk[vx])
		for(int i=vx,R=rad[vx];R>0;i = par[i], R--){
			op[i].pb({R,1});
			if(i && R > 1) op[i].pb({R-2,-1});
			if(i == 0) break;
		}
}

main(){

	int nt;
	scanf("%d",&nt);
	while(nt--){

		int k;
		scanf("%d%d",&n,&k);

		for(int i=0;i<n;i++)
			L[i].clear(), op[i].clear(), mrk[i] = 0;

		for(int i=0;i<=2*n+2;i++) T[0][i] = T[1][i] = 0;
		
		for(int i=0;i<n-1;i++){
			int a,b;
			scanf("%d%d",&a,&b), a--, b--;
			L[a].pb(b);
			L[b].pb(a);
		}

		for(int i=0;i<k;i++){
			int c,r;
			scanf("%d%d",&c,&r), c--;
			mrk[c] = 1;
			rad[c] = r;
		}

		dfs(0);
		calc(0);

		for(int i=0;i<n;i++)
			printf("%d%c",ans[i]," \n"[i==n-1]);

	}

}

Tester's Solution

#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#ifndef rd
#define trace(...)
#define endl '\n'
#endif
#define pb push_back
#define fi first
#define se second
#define int long long
typedef long long ll;
typedef long double f80;
#define double long double
#define pii pair<int,int>
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int infi=0x3f3f3f3f;
//const int mod=998244353;
const int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
 
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
	uniform_int_distribution<int> uid(0,lim-1);
	return uid(rang);
}
 
long long readInt(long long l,long long r,char endd){
	long long x=0;
	int cnt=0;
	int fi=-1;
	bool is_neg=false;
	while(true){
		char g=getchar();
		if(g=='-'){
			assert(fi==-1);
			is_neg=true;
			continue;
		}
		if('0'<=g && g<='9'){
			x*=10;
			x+=g-'0';
			if(cnt==0){
				fi=g-'0';
			}
			cnt++;
			assert(fi!=0 || cnt==1);
			assert(fi!=0 || is_neg==false);
 
			assert(!(cnt>19 || ( cnt==19 && fi>1) ));
		} else if(g==endd){
			if(is_neg){
				x= -x;
			}
			assert(l<=x && x<=r);
			return x;
		} else {
			assert(false);
		}
	}
}
string readString(int l,int r,char endd){
	string ret="";
	int cnt=0;
	while(true){
		char g=getchar();
		assert(g!=-1);
		if(g==endd){
			break;
		}
		cnt++;
		ret+=g;
	}
	assert(l<=cnt && cnt<=r);
	return ret;
}
long long readIntSp(long long l,long long r){
	return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
	return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
	return readString(l,r,'\n');
}
string readStringSp(int l,int r){
	return readString(l,r,' ');
}
 
 
vi gra[800005];
pii tr[1600005];
int par[800005];
int depth[800005];
int dsu[800005];
int fpar(int u) {
	return (dsu[u]<0)?u:dsu[u]=fpar(dsu[u]);
}
void merge(int u, int v) {
	if((u=fpar(u))!=(v=fpar(v))) {
		if(dsu[u]>dsu[v])
			swap(u,v);
		dsu[u]+=dsu[v];
		dsu[v]=u;
	}
}
 
void sz_dfs(int fr, int at) {
	depth[at]=depth[fr]+1;
	par[at]=fr;
	for(int i:gra[at])
		if(i!=fr)
			sz_dfs(at,i);
}
vector<pii> upds[800005];
int ans[800005],n;
void update(int p, pii hol) {
	p+=n;
	for(tr[p].fi+=hol.fi,tr[p].se+=hol.se; p>1; p>>=1)
		tr[p>>1]={tr[p].fi+tr[p^1].fi,tr[p].se+tr[p^1].se};
}
pii get(int l, int r) {
	r++;
	pii res={0,0};
	for(l+=n,r+=n; l<r; l>>=1,r>>=1) {
		if(l&1) {
			res.fi+=tr[l].fi,res.se+=tr[l].se;
			l++;
		}
		if(r&1) {
			r--;
			res.fi+=tr[r].fi,res.se+=tr[r].se;
		}
	}
	return res;
}
void dfs(int fr, int at) {
	for(auto i:upds[at]) {
		if(i.se>0)
			update(min(n,i.fi),{i.fi+1,i.se});
		else
			update(min(n,i.fi),{-(i.fi+1),i.se});
	}
	pii pool=get(depth[at],n);
	trace(at,pool);
	ans[at]=pool.fi-pool.se*depth[at];
	for(int i:gra[at])
		if(i!=fr)
			dfs(at,i);
	for(auto i:upds[at]) {
		if(i.se>0)
			update(min(n,i.fi),{-i.fi-1,-i.se});
		else
			update(min(n,i.fi),{i.fi+1,-i.se});
	}
}
int sum_n=0;
void solve() {
	int k;
	n=readIntSp(1,800000);
	memset(dsu,-1,sizeof(int)*(n+5));
	sum_n+=n;
	k=readIntLn(1,n);
	fr(i,1,n) {
		gra[i].clear();
		upds[i].clear();
	}
	fr(i,2,n) {
		int u=readIntSp(1,n),v=readIntLn(1,n);
		assert(u!=v);
		merge(u,v);
		gra[u].pb(v);
		gra[v].pb(u);
	}
	assert(dsu[fpar(1)]==-n);
	sz_dfs(0,1);
	vi vs;
	fr(i,1,k) {
		int v,r;
		v=readIntSp(1,n);
		r=readIntLn(1,n);
		vs.pb(v);
		upds[v].pb({r+depth[v]-1,1});
		r--;
		while(par[v]!=0&&r>0) {
			upds[v].pb({r+depth[v]-2,-1});
			upds[par[v]].pb({r+depth[v]-2,1});
			v=par[v];
			r--;
		}
	}
	sort(all(vs));
	vs.resize(unique(all(vs))-vs.begin());
	assert(sz(vs)==k);
	dfs(1,1);
	fr(i,1,n)
		cout<<ans[i]<<" ";
	cout<<endl;
}
signed main() {
	ios_base::sync_with_stdio(0),cin.tie(0);
	srand(chrono::high_resolution_clock::now().time_since_epoch().count());
	cout<<fixed<<setprecision(8);
	int t=readIntLn(1,2000);
//	cin>>t;
	while(t--)
		solve();
	assert(1<=sum_n&&sum_n<=800000);
	assert(getchar()==EOF);
	return 0;
}

Editorialist's Solution

#include <bits/stdc++.h>
using namespace std;

struct BIT {
	vector<long long> arr;
	void init(long long s = 1e6) {
		arr.assign(s+1 , 0);
	}
	long long sum(long long pos) {
		long long ans = 0;
		while(pos > 0) {
			ans += arr[pos];
			pos = pos - (pos & (-pos));
		}
		return ans;
	}
	void update(long long pos, long long val) {
		while((pos > 0) && (pos < arr.size())) {
			arr[pos] += val;
			pos = pos + (pos & (-pos));
		}
	}
	long long rQuery(long long l, long long r) {
		return sum(r) - sum(l-1);
	}
};

int N, K;
vector<vector<int>> graph;
vector<vector<pair<long long, long long>>> updates; // in pair it stores {value to be added, number of times it should be added}.
vector<int> parent, depth;
vector<long long> ans;
BIT sum_depths, count_depths;

void computeDetails(int node, int par, int _depth) { // function is used to compute parent and depth of each node when we root the tree at node 1.
	parent[node] = par;
	depth[node] = _depth;
	for(auto to : graph[node]) {
		if(to == par) continue;
		computeDetails(to, node, _depth+1);
	}
}

void computeAnswer(int node, int par) {
	for(auto i : updates[node]) { // adding the effect of updates for the node, as it will effect the nodes in its subtree.
		long long value = depth[node] + i.first;
		long long count = i.second; 
		sum_depths.update(value, count*value); // as this value will impact only those nodes which have depths < value.
		count_depths.update(value, count);
	}
	// computing the answer for the current node.
	// security value of node = sum_of_updates(with value greater than equal to its depth) - (depth[node] * count_of_updates(with value greater than equal to its depth));
	long long sum_of_updates = sum_depths.rQuery(depth[node], 2*N+5); // as all the lower values do note 
	long long count_of_updates = count_depths.rQuery(depth[node], 2*N+5);
	ans[node] = sum_of_updates - (depth[node] * count_of_updates);

	for(auto to : graph[node]) { // computing answer for nodes in its subtree.
		if(to == par) continue;
		computeAnswer(to, node);
	}

	for(auto i : updates[node]) { // removing the effect of updates for the node, as answer for all nodes in it's subtree is computed.
		long long value = depth[node] + i.first;
		long long count = -i.second; 
		sum_depths.update(value, count*value); // as this value will impact only those nodes which have depths < value.
		count_depths.update(value, count);
	}
}

void solveTestCase() {
	cin >> N >> K;

	updates.clear();
	updates.resize(N+1);
	ans.assign(N+1, 0);
	graph.clear();
	graph.resize(N+1);
	parent.resize(N+1);
	depth.resize(N+1);

	// In the below BIT's the index represent value of update.
	sum_depths.init(2*N+5); // This BIT maintains the sum of security values at each depth for each vertex(it can be maintained for each vertex because we modify it as we go up and down the dfs).
	count_depths.init(2*N+5); // This BIT maintains the count of updates at each depth and is used to count the number of times a vertex is updated(used to compute the answer). It can be maintained for each vertex because we modify it as we go up and down the dfs.

	for(int i = 1; i <= N-1; i ++) {
		int a, b;
		cin >> a >> b;
		graph[a].push_back(b);
		graph[b].push_back(a);
	}

	computeDetails(1, -1, 1); // rooting the tree at 1.

	for(int i = 1; i <= K; i ++) {
		int station, radious;  // V_i, R_i
		cin >> station >> radious;
		// Now we have to properly add updates so that we can compute our answer.
		updates[station].push_back({radious, 1}); // as we add values to its subtree.
		while((parent[station] != -1) && (radious > 1)) { 
			radious --; // as its parent is at distance 1 from its child
			updates[parent[station]].push_back({radious, 1}); // as we add values to subtree of parent[station].
			if(radious > 1) { // but we don't want to add the values to subtree of station again as we have already added so to negate the effect of parent flag
				updates[station].push_back({radious-1, -1});
			}
			station = parent[station];
		}
	}

	computeAnswer(1, -1);

	for(int i = 1; i <= N; i ++) {
		cout << ans[i] << " ";
	}
	cout << '\n';
}

int main() {
	ios_base::sync_with_stdio(0); // fast IO
	cin.tie(0);
	cout.tie(0);

	int testCase;
	cin >> testCase;
	for(int i = 1; i <= testCase; i ++) {
		solveTestCase();
	}

}

Video Editorial

Feel free to share your approach. In case of any doubt or anything is unclear please ask it in the comment section. Any suggestions are welcomed.

errichto · September 11, 2020, 6:22pm

This is a standard centroid-decomposiion problem even without the condition S[V[i]] = R[i].

psychik · September 12, 2020, 9:14pm

Will it not be O(N*log^2N) ?