PROBLEM LINK:
Practice
Div-3 Contest
Div-2 Contest
Div-1 Contest
Author & Editorialist : Shruti Agrawal
Testers : Shubham Jain, Aryan Choudhary
DIFFICULTY:
SIMPLE
PREREQUISITES:
Implementation, Modulus, Math
PROBLEM:
Chef has N 6-sided standard dice. Each die has dimensions 1×1×1. First, Chef forms four vertical stacks of dice on his table, which together make up a pile of dice with a base area up to 2×2. Among all such structures, the total visible surface area of Chef’s structure must be the smallest possible.
Then, Chef calculates the number of pips on the visible faces of all dice in the structure. Among all possible arrangements of dice, what is the maximum possible total number of visible pips?
QUICK EXPLANATION:
For minimum visible area, dice should be stacked together, 4 dice in a level.
If 4 is not possible then arranged as such they share a face to minimize the visible surface area.
Each dice must be kept in such a way that the faces with more pips are visible.
EXPLANATION:
For minimum visible area, dice should be stacked together, 4 dice in a level.
Only at the topmost level, it can be less than 4 dice, or only if N<4.
In other words, if there are N dice then floor(N/4) levels would be there with 4 dice at each level.
if N%4 != 0, then there would be a level with less than 4 (i.e. N%4) dice.
In the top tier, the dice should be arranged as such they share a face with each other for minimizing the visible surface area.
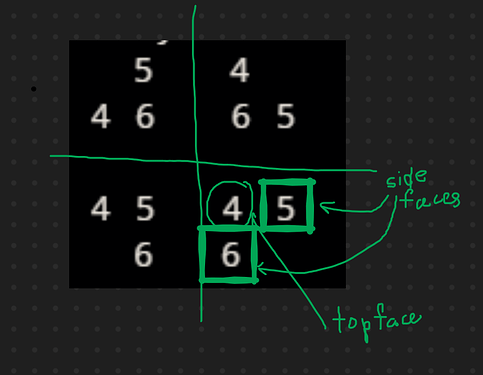
For any dice,
if 5 faces are visible, then the values should be 6, 5, 4, 3, 2.
if 4 faces are visible, then the values should be 6, 5, 4, 3.
if 3 faces are visible, then the values should be 6, 5, 4.
if 2 faces are visible, then the values should be 6, 5.
For example,
If N = 4, then the number of visible faces in each dice is 3. So, the total number of pips in the structure would be 4*(6+5+4), which is equal to 60.
SUBTASK 1:
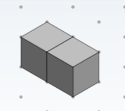 N = 2
N = 2 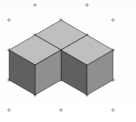 N = 3
N = 3  N = 4
N = 4
SUBTASK 2:
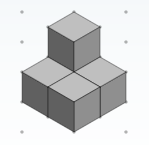 N = 5
N = 5 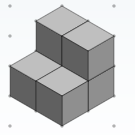 N = 6
N = 6 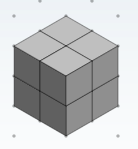 N = 8
N = 8
SUBTASK 3:
 N = 9
N = 9  N = 10
N = 10  N = 11
N = 11
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
#define ll long long int
int main(){
int i,j,k,t;
cin>>t;
while(t--){
ll n;
cin>>n;
ll ans=0;
if(n%4==1){
ans=20;
}
if(n%4==2){
ans=36;
}
if(n%4==3){
ans=51;
}
ll times=n/4LL;
ans+=times*44LL;
if(times>=1){
ans+=(4LL*(ll)(4-n%4));
}
cout<<ans<<"\n";
}
return 0;
}
Tester's Solution
//Author - Aryan (@aryanc403)
#ifdef ARYANC403
#include <header.h>
#else
#pragma GCC optimize ("Ofast")
#pragma GCC target ("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx")
//#pragma GCC optimize ("-ffloat-store")
#include<bits/stdc++.h>
#define dbg(args...) 42;
#endif
using namespace std;
#define fo(i,n) for(i=0;i<(n);++i)
#define repA(i,j,n) for(i=(j);i<=(n);++i)
#define repD(i,j,n) for(i=(j);i>=(n);--i)
#define all(x) begin(x), end(x)
#define sz(x) ((lli)(x).size())
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#define endl "\n"
typedef long long int lli;
typedef long double mytype;
typedef pair<lli,lli> ii;
typedef vector<ii> vii;
typedef vector<lli> vi;
const auto start_time = std::chrono::high_resolution_clock::now();
void aryanc403()
{
#ifdef ARYANC403
auto end_time = std::chrono::high_resolution_clock::now();
std::chrono::duration<double> diff = end_time-start_time;
cerr<<"Time Taken : "<<diff.count()<<"\n";
#endif
}
long long readInt(long long l, long long r, char endd) {
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true) {
char g=getchar();
if(g=='-') {
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g&&g<='9') {
x*=10;
x+=g-'0';
if(cnt==0) {
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd) {
if(is_neg) {
x=-x;
}
assert(l<=x&&x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret="";
int cnt=0;
while(true) {
char g=getchar();
assert(g!=-1);
if(g==endd) {
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt&&cnt<=r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l,r,' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l,r,'\n');
}
string readStringLn(int l, int r) {
return readString(l,r,'\n');
}
string readStringSp(int l, int r) {
return readString(l,r,' ');
}
void readEOF(){
assert(getchar()==EOF);
}
vi readVectorInt(lli l,lli r,int n){
vi a(n);
for(int i=0;i<n-1;++i)
a[i]=readIntSp(l,r);
a[n-1]=readIntLn(l,r);
return a;
}
const lli INF = 0xFFFFFFFFFFFFFFFL;
lli seed;
mt19937 rng(seed=chrono::steady_clock::now().time_since_epoch().count());
inline lli rnd(lli l=0,lli r=INF)
{return uniform_int_distribution<lli>(l,r)(rng);}
class CMP
{public:
bool operator()(ii a , ii b) //For min priority_queue .
{ return ! ( a.X < b.X || ( a.X==b.X && a.Y <= b.Y )); }};
void add( map<lli,lli> &m, lli x,lli cnt=1)
{
auto jt=m.find(x);
if(jt==m.end()) m.insert({x,cnt});
else jt->Y+=cnt;
}
void del( map<lli,lli> &m, lli x,lli cnt=1)
{
auto jt=m.find(x);
if(jt->Y<=cnt) m.erase(jt);
else jt->Y-=cnt;
}
bool cmp(const ii &a,const ii &b)
{
return a.X<b.X||(a.X==b.X&&a.Y<b.Y);
}
const lli mod = 1000000007L;
// const lli maxN = 1000000007L;
lli T,n,i,j,k,in,cnt,l,r,u,v,x,y;
lli m;
string s;
const vi a={0,20,36,51,60,20+44+12,36+44+8,51+44+4,60+44};
//priority_queue < ii , vector < ii > , CMP > pq;// min priority_queue .
int main(void) {
ios_base::sync_with_stdio(false);cin.tie(NULL);
// freopen("txt.in", "r", stdin);
// freopen("txt.out", "w", stdout);
// cout<<std::fixed<<std::setprecision(35);
dbg(a);
T=readIntLn(1,1e5);
while(T--)
{
n=readIntLn(1,1e12);
if(n<=8)
cout<<a[n]<<endl;
else
{
const lli l=(n/4)-1;
n&=3;n+=4;
cout<<a[n]+l*44<<endl;
}
} aryanc403();
readEOF();
return 0;
}