PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Erfan Alimohammadi
Tester: Aleksa Plasvic
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy
PREREQUISITES:
Bitmasks, Implementation.
PROBLEM:
Given a digital display where each single decimal digit is represented by seven segments. Some of the segments are broken. We are also given N conditions, where each condition specifies that when we try to show value x, exactly y segments switch to on state. We need to find the minimum and the maximum number of segments which can be broken so that all the conditions are satisfied, or print invalid if no possible set of broken segments can satisfy the given conditions.
QUICK EXPLANATION
- Since there are seven segments and each segment can be either broken or non-broken, there can be 2^7 different compositions.
- For checking each configuration, we can check manually whether the number of segments in on state is exactly same as given in condition for all digits. If the configuration is valid for each digit, we can consider the number of broken segments in our minimum and maximum and then finally print these values. In case we do not find any valid configuration, we should print Invalid.
- For ease of implementation, bitmasks can be used, each bit denoting one of the seven segments and bit being on or off tells the state of the segment.
EXPLANATION
Let us denote configuration of the display as assigning each segment either working or broken. Since each segment can be in one of the two states, the total number of configurations can be 2^7 = 128.
Since the number of configurations is small, we can try each configuration and check if this configuration is valid or not. If it is valid, we can consider the number of broken segments and print the minimum and maximum of this value over all valid configurations.
Now, the only part left is, that how to check whether a given configuration is valid for the given set of conditions.
Let us denote each segment by bits. So, each configuration can be written as a binary number with exactly seven bit, ith bit denoting the state of ith segment, if we number the bits as shown in the image.
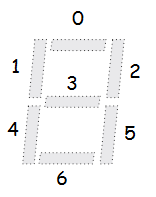
Now, the segments which shall try to be in on state for a given digit can also be written as a binary number mask of digit x. How to find out the number of segments in on state, if we have to display x for a given configuration given by binary number mask.
We know, ith segment shall be in on state IF and only if the ith bit in both the configuration and mask have the ith bit on. This is the same as AND bitwise operation. Hence, we can just take the AND value of configuration and mask of digit and check if the number of set bits is the same as given in condition or not.
Hence, we can pre-define masks of each digit and check all configurations.
You can refer this to learn more on bitwise algorithms.
Time Complexity
Time complexity is O(N*2^7*7) per test case.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
int mask[10]={119, 36, 93, 109, 46, 107, 123, 37, 127, 111};
int n;
int x[11], y[11];
int check(int msk)
{
for (int i=1;i<=n;i++)
{
int bed = 0;
for (int j=0;j<7;j++)
if ((mask[x[i]]&(1<<j)) && !(msk&(1<<j))) bed++;
if (bed!=y[i]) return false;
}
return true;
}
void solve()
{
assert(n<=10);
cin>>n;
for (int i=1;i<=n;i++){
cin>>x[i]>>y[i];
assert(x[i]>=0 && x[i]<=9);
assert(y[i]<=7 && y[i]>=0);
for (int j=i-1;j>0;j--)
assert(x[i]!=x[j]);
}
int ok = 0;
int mini = 10;
int maxi = 0;
for (int i=0;i<1<<7;i++)
if (check(i)){
if (!ok)
{
ok = 1;
mini = __builtin_popcount(i);
maxi = mini;
} else
{
mini = min(mini, __builtin_popcount(i));
maxi = max(maxi, __builtin_popcount(i));
}
}
if (!ok) printf("invalid\n"); else
printf("%d %d\n",mini,maxi);
}
int main()
{
int t;
cin>>t;
while(t--)
solve();
return 0;
}
Tester's Solution
#include<bits/stdc++.h>
using namespace std;
int mask[10]={119, 36, 93, 109, 46, 107, 123, 37, 127, 111};
int n;
int x[11], y[11];
int check(int msk)
{
for (int i=1;i<=n;i++)
{
int bed = 0;
for (int j=0;j<7;j++)
if ((mask[x[i]]&(1<<j)) && !(msk&(1<<j))) bed++;
if (bed!=y[i]) return false;
}
return true;
}
void solve()
{
assert(n<=10);
cin>>n;
for (int i=1;i<=n;i++){
cin>>x[i]>>y[i];
assert(x[i]>=0 && x[i]<=9);
assert(y[i]<=7 && y[i]>=0);
for (int j=i-1;j>0;j--)
assert(x[i]!=x[j]);
}
int ok = 0;
int mini = 10;
int maxi = 0;
for (int i=0;i<1<<7;i++)
if (check(i)){
if (!ok)
{
ok = 1;
mini = __builtin_popcount(i);
maxi = mini;
} else
{
mini = min(mini, __builtin_popcount(i));
maxi = max(maxi, __builtin_popcount(i));
}
}
if (!ok) printf("invalid\n"); else
printf("%d %d\n",mini,maxi);
}
int main()
{
int t;
cin>>t;
assert(t<=1000);
while(t--)
solve();
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
//Solution Credits: Taranpreet Singh
class SEVENSEG{
//SOLUTION BEGIN
void pre() throws Exception{}
// _ 0
//| | 1 2
// _ 3
//| | 4 5
// _ 6
int get(int[] x){
int ans = 0;
for(int y:x)ans |= 1<<y;
return ans;
}
void solve(int TC) throws Exception{
int[] cur = new int[10];
cur[0] = get(new int[]{0,1,2,4,5,6});
cur[1] = get(new int[]{2,5});
cur[2] = get(new int[]{0,2,3,4,6});
cur[3] = get(new int[]{0,2,3,5,6});
cur[4] = get(new int[]{1,2,3,5});
cur[5] = get(new int[]{0,1,3,5,6});
cur[6] = get(new int[]{0,1,3,4,5,6});
cur[7] = get(new int[]{0,2,5});
cur[8] = get(new int[]{0,1,2,3,4,5,6});
cur[9] = get(new int[]{0,1,2,3,5,6});
int n = ni();
int[] val = new int[10];
Arrays.fill(val, -1);
boolean valid = true;
for(int i = 0; i< n; i++){
int x = ni(), y = ni();
if(val[x]==-1)val[x] = y;
else valid &= val[x]==y;
}
int min = 8, max = -1;
for(int i = 0; i< 1<<7; i++){
boolean v = true;
for(int j = 0; j< 10; j++){
if(val[j]==-1)continue;
if(bit(i&cur[j])!=val[j])v = false;
}
if(v){
min = Math.min(min, 7-bit(i));
max = Math.max(max, 7-bit(i));
}
}
if(valid && min<= max)pn(min+" "+max);
else pn("invalid");
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
long mod = (long)1e9+7, IINF = (long)1e18;
final int INF = (int)1e9, MX = (int)3e5+2;
DecimalFormat df = new DecimalFormat("0.00000000000");
double PI = 3.1415926535897932384626433832792884197169399375105820974944, eps = 1e-8;
static boolean multipleTC = true, memory = false;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
int T = (multipleTC)?ni():1;
//Solution Credits: Taranpreet Singh
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
if(memory)new Thread(null, new Runnable() {public void run(){try{new SEVENSEG().run();}catch(Exception e){e.printStackTrace();}}}, "1", 1 << 28).start();
else new SEVENSEG().run();
}
long gcd(long a, long b){return (b==0)?a:gcd(b,a%b);}
int gcd(int a, int b){return (b==0)?a:gcd(b,a%b);}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()

 Hope this Helps
Hope this Helps