PROBLEM LINK:
Contest - Division 3
Contest - Division 2
Contest - Division 1
Setter: Prasanna Kumar
Tester: Anshu Garg, Nishant Shah
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
PROBLEM:
Given a rooted tree with N nodes. Initially, all nodes have colour black. You are also given Q queries of the following form:
- Determine the number of paths passing through edge u\to v, with both endpoint nodes having the colour black.
- Invert the colour of all nodes in the subtree of node u.
EXPLANATION:
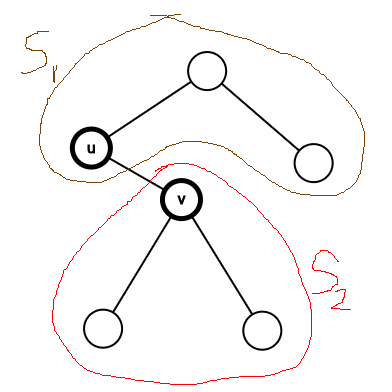
(Leonardo gave the world ‘Mona Lisa’; here’s my masterpiece ![]() )
)
Let b_1 and b_2 correspond to the number of black nodes in S_1 and S_2 (from above picture), respectively. For queries of type 1, the answer is equal to
where b_1+b_2 is equivalent to the number of black nodes in the whole graph.
Thus we have reduced the problem to:
- Invert the color of all nodes in the subtree of u
- Determine the number of black nodes in the subtree of u (and subtree of node 1 - to find the total number of black nodes).
This can be solved efficiently using a Segment Tree (with lazy propagation) on the Euler Tour of the rooted tree.
How?
Run Euler Tour on the tree; let tin_u and tout_v be the entry and exit times of node u in the tour.
Consider an array A such that A_{tin_u} = 1 if node u is black. Initially, A_i = 1 for all valid i.
- For a flip operation (query type 2) on the subtree of u, invert the value of all elements of A in the range [tin_u, tout_u].
- To query the number of black nodes in the subtree of u, sum all elements of A in the range [tin_u, tout_u].
Both operations can be done in O(\log N) per query, using segment trees with lazy propagation.
TIME COMPLEXITY:
Running Euler Tour takes O(N). Building the segment tree takes O(N\log N). Each query takes O(\log N). The total complexity is thus:
SOLUTIONS:
Editorialist’s solution can be found here
Experimental: For evaluation purposes, please rate the editorial (1 being poor and 5 excellent)
- 1
- 2
- 3
- 4
- 5
0 voters