PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author: kryptonix171
Tester: mexomerf
Editorialist: iceknight1093
DIFFICULTY:
TBD
PREREQUISITES:
DP
PROBLEM:
You’re given an N\times M grid, with A_{i, j} denoting who between two players shot at each cell.
If cell (x, y) is the bullseye, the score of shooting at cell (x_1, y_1) is \max(|x-x_1|, |y-y_1|).
The score of a player is the sum of all their scores.
For each of the N\cdot M cells, find the difference between the scores of both players, if that cell was the bullseye.
EXPLANATION:
Unlike the easy version, we do need to consider both dimensions now.
However, the core idea behind the solution is remarkably similar - compute the score of each cell for each player individually, then find their difference at the end.
So, let’s look at just the first player.
Suppose we’re currently at cell (x, y), and we know the score if this is the bullseye.
Let’s analyze how the cost changes when we move to cell (x, y+1), i.e, move one cell right.
Look at some cell (x_1, y_1) that’s to the ‘right’ of (x, y), i.e, with y_1 \gt y.
When at (x, y), the score of shooting this was \max(|x-x_1|, y_1-y).
After we move one cell to the right, the new score is \max(|x-x_1|, y_1-y-1).
Notably, the distance along the y-coordinate decreased.
So,
- If |x-x_1| \geq y_1 - y, then |x-x_1| \gt y_1-y-1 and so the score of this cell actually doesn’t change - and remains |x-x_1|.
- If |x-x_1| \lt y_1 - y, then |x-x_1| \leq y_1-y-1, and so \max(|x-x_1|, y_1-y-1) = y_1-y-1.
In other words, the score of shooting such a cell in fact decreased by 1.
Similarly, analyzing cells on the ‘left’ of (x, y) (i.e, with y_1 \leq y), it can be seen that if |x-x_1| \leq y-y_1 then the score will increase by 1; otherwise it doesn’t change.
This means, to compute the change in score, all we want to know is the number of shot cells (x_1, y_1) such that:
- y_1 \gt y and |x-x_1| \lt y_1 - y; or
- y_1 \leq y and |x-x_1| \leq y_1 - y.
To do this, it helps to actually visualize what’s going on.
If you color the respective areas, you’ll end up with the following:
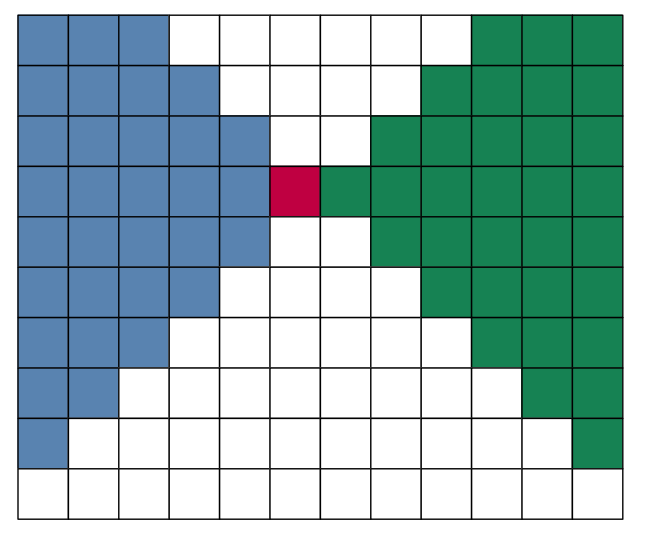
In the above image, the red cell is (x, y).
The area colored green encompasses the cells satisfying y_1 \gt y and |x-x_1| \lt y_1 - y, and
the area colored blue (along with the red cell) marks cells satisfying y_1 \leq y and |x-x_1| \leq y_1 - y.
What we want to know is essentially, “how many cells in the green/blue area did this player shoot at?”
Notice that these areas look quite triangular: just that they’re tilted sideways.
So, all we need to be able to do, is quickly find sums in such triangular areas.
This is doable with dynamic programming (in similar fashion to 2D prefix sums).
Details
Let’s see how to compute the green area: everything else is similar.
Let s_{i, j} be either 0 or 1, depending on whether the current player shot cell (i, j).
Define \text{right}[i][j] to be the sum of values of s of cells in the green area, if (i, j) is the left tip of the triangle.
Let’s try to compute this from smaller triangles.
To start off, we have s_{i, j} itself, along with the triangles from cells (i-1, j+1), (i, j+1), (i+1, j+1).
Adding them all together overcounts certain areas though, so we need to subtract out stuff.
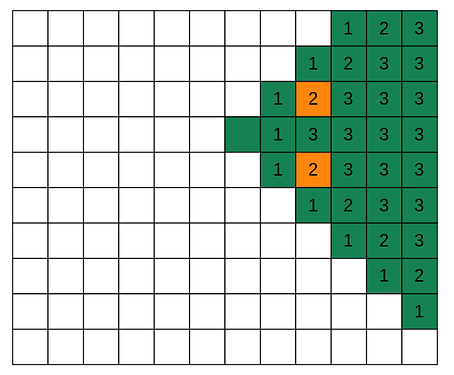
In particular, we see that the number of times each cell was added is something like this:
The number in each cell is the number of times it’s been added.
We want all of these values to be 1 (and not 2 or 3).
For that, we can subtract out the triangles with tips at (i-1, j+2) and (i+1, j+2) - namely, the ones colored orange.
This leaves just the cell (i, j+2) counted thrice, so it can be subtracted out too.
So, we obtain
Some of these cells may not exist if you’re close to a border, those values can be treated as just 0 (but do take care to not make out of bounds accesses - the simplest way to do this is to just pad the grid with a couple layers of zeros, so that you don’t need a million checks).
The leftward triangle sums can be computed similarly, the analysis is in fact exactly the same.
With these sums precomputed, we can move from (x, y) to (x, y+1) and update the score in
\mathcal{O}(1) time.
By similarly computing sums of upward and downward triangles, we can move from (x, y) to (x+1, y) in constant time.
That allows us to now compute all the answers as follows:
- Compute the answer for (1, 1) somehow, say by just iterating across all N\times M cells directly.
- Use the left/right triangles to move from (1, 1) to (1, 2), then to (1, 3), and so on till (1, M), all in constant time.
- Use the up/down triangles to move to (2, 1) from (1, 1), and then again move rightward along this row.
- Move from (2, 1) to (3, 1), then solve for the third row, and so on.
Repeat this till all N rows have been taken care of.
TIME COMPLEXITY:
\mathcal{O}(N\cdot M) per testcase.
CODE:
Author's code (C++)
#include <bits/stdc++.h>
#define int long long int
#define debug cout<<"K"
#define mod 1000000007
using namespace std;
void right(int n, int m, vector<vector<int>>&mat, vector<vector<int>>&dp3, int x, vector<vector<int>>&dp1,vector<vector<int>>&dp2)
{
//int dp1[n][m]={0};
//int dp2[n][m]={0};
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=m-1;j>=0;j--)
{
dp1[i][j]=0;dp2[i][j]=0;
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp1[i][j]=cnt;
if(i-1>=0&&j+1<m)
dp1[i][j]+=dp1[i-1][j+1];
}
}
for(int i=n-1;i>=0;i--)
{
int cnt=0;
for(int j=m-1;j>=0;j--)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp2[i][j]=cnt;
if(i+1<n&&j+1<m)
dp2[i][j]+=dp2[i+1][j+1];
}
}
for(int i=n-1;i>=0;i--)
{
int cnt=0;
for(int j=m-1;j>=0;j--)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp3[i][j]=cnt;
if(i+1<n&&j+1<m)
dp3[i][j]+=dp2[i+1][j+1];
if(i-1>=0&&j+1<m)
dp3[i][j]+=dp1[i-1][j+1];
}
}
}
void left(int n, int m, vector<vector<int>>&mat, vector<vector<int>>&dp3, int x, vector<vector<int>>&dp1,vector<vector<int>>&dp2)
{
//int dp1[n][m]={0};
//int dp2[n][m]={0};
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=0;j<m;j++)
{
dp1[i][j]=0;dp2[i][j]=0;
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp1[i][j]=cnt;
if(i-1>=0&&j-1>=0)
dp1[i][j]+=dp1[i-1][j-1];
}
}
for(int i=n-1;i>=0;i--)
{
int cnt=0;
for(int j=0;j<m;j++)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp2[i][j]=cnt;
if(i+1<n&&j-1>=0)
dp2[i][j]+=dp2[i+1][j-1];
}
}
for(int i=n-1;i>=0;i--)
{
int cnt=0;
for(int j=0;j<m;j++)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp3[i][j]=cnt;
if(i+1<n&&j-1>=0)
dp3[i][j]+=dp2[i+1][j-1];
if(i-1>=0&&j-1>=0)
dp3[i][j]+=dp1[i-1][j-1];
}
}
}
void up(int n, int m, vector<vector<int>>&mat, vector<vector<int>>&dp3, int x, vector<vector<int>>&dp1,vector<vector<int>>&dp2)
{
//int dp1[n][m]={0};
//int dp2[n][m]={0};
for(int j=0;j<m;j++)
{
int cnt=0;
for(int i=0;i<n;i++)
{
dp1[i][j]=0;dp2[i][j]=0;
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp1[i][j]=cnt;
if(i-1>=0&&j-1>=0)
dp1[i][j]+=dp1[i-1][j-1];
}
}
for(int j=m-1;j>=0;j--)
{
int cnt=0;
for(int i=0;i<n;i++)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp2[i][j]=cnt;
if(i-1>=0&&j+1<m)
dp2[i][j]+=dp2[i-1][j+1];
}
}
for(int j=m-1;j>=0;j--)
{
int cnt=0;
for(int i=0;i<n;i++)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp3[i][j]=cnt;
if(i-1>=0&&j+1<m)
dp3[i][j]+=dp2[i-1][j+1];
if(i-1>=0&&j-1>=0)
dp3[i][j]+=dp1[i-1][j-1];
}
}
}
void down(int n, int m, vector<vector<int>>&mat, vector<vector<int>>&dp3, int x, vector<vector<int>>&dp1,vector<vector<int>>&dp2)
{
//int dp1[n][m]={0};
//int dp2[n][m]={0};
for(int j=0;j<m;j++)
{
int cnt=0;
for(int i=n-1;i>=0;i--)
{
dp1[i][j]=0;dp2[i][j]=0;
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp1[i][j]=cnt;
if(i+1<n&&j-1>=0)
dp1[i][j]+=dp1[i+1][j-1];
}
}
for(int j=m-1;j>=0;j--)
{
int cnt=0;
for(int i=n-1;i>=0;i--)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp2[i][j]=cnt;
if(i+1<n&&j+1<m)
dp2[i][j]+=dp2[i+1][j+1];
}
}
for(int j=m-1;j>=0;j--)
{
int cnt=0;
for(int i=n-1;i>=0;i--)
{
if(mat[i][j]==x||mat[i][j]==3)
{
cnt++;
}
dp3[i][j]=cnt;
if(i+1<n&&j+1<m)
dp3[i][j]+=dp2[i+1][j+1];
if(i+1<n&&j-1>=0)
dp3[i][j]+=dp1[i+1][j-1];
}
}
}
int32_t main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin>>t;
while(t--)
{
int n,m;
cin>>n>>m;
vector<vector<int>>dp1;
vector<vector<int>>dp2;
vector<vector<int>>v;
vector<vector<int>>dpright1;
vector<vector<int>>dpright2;
vector<vector<int>>dpleft1;
vector<vector<int>>dpleft2;
vector<vector<int>>dpup1;
vector<vector<int>>dpup2;
vector<vector<int>>dpdown1;
vector<vector<int>>dpdown2;
for(int i=0;i<n;i++)
{
vector<int>a;
for(int j=0;j<m;j++)
{
int q;
cin>>q;
a.push_back(q);
}
v.push_back(a);
vector<int>b(m,0);
dpright1.push_back(b);
dpright2.push_back(b);
dpleft1.push_back(b);
dpleft2.push_back(b);
dpup1.push_back(b);
dpup2.push_back(b);
dpdown1.push_back(b);
dpdown2.push_back(b);
dp1.push_back(b);
dp2.push_back(b);
}
right(n,m,v,dpright1,1,dp1,dp2);
right(n,m,v,dpright2,2,dp1,dp2);
left(n,m,v,dpleft1,1,dp1,dp2);
left(n,m,v,dpleft2,2,dp1,dp2);
up(n,m,v,dpup1,1,dp1,dp2);
up(n,m,v,dpup2,2,dp1,dp2);
down(n,m,v,dpdown1,1,dp1,dp2);
down(n,m,v,dpdown2,2,dp1,dp2);
int x=0;
int y=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(v[i][j]==1||v[i][j]==3)
x+=max(llabs(0-i),llabs(0-j));
if(v[i][j]==2||v[i][j]==3)
y+=max(llabs(0-i),llabs(0-j));
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
dp1[i][j]=0;
dp2[i][j]=0;
}
}
dp1[0][0]=x;
dp2[0][0]=y;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(i==0&&j==0)
continue;
if(j==0)
{
dp1[i][j]=dp1[i-1][j];
dp1[i][j]-=dpdown1[i][j];
dp1[i][j]+=dpup1[i-1][j];
dp2[i][j]=dp2[i-1][j];
dp2[i][j]-=dpdown2[i][j];
dp2[i][j]+=dpup2[i-1][j];
}
else
{
dp1[i][j]=dp1[i][j-1];
dp1[i][j]-=dpright1[i][j];
dp1[i][j]+=dpleft1[i][j-1];
dp2[i][j]=dp2[i][j-1];
dp2[i][j]-=dpright2[i][j];
dp2[i][j]+=dpleft2[i][j-1];
}
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cout<<llabs(dp1[i][j]-dp2[i][j])<<" ";
}
cout<<"\n";
}
}
return 0;
}
Tester's code (C++)
#include <bits/stdc++.h>
using namespace std;
#define int long long
void cal(vector<int> a[], vector<int> pr[], vector<int> sf[], vector<int> up[], vector<int> dw[], int n, int m){
int prr[n][m][2] = {}, sff[n][m][2] = {}, upp[n][m][2] = {}, dww[n][m][2] = {};
for(int i = 0; i < m; i++){
pr[0][i] = a[0][i];
prr[0][i][0] = prr[0][i][1] = a[0][i];
sf[n - 1][i] = a[n - 1][i];
sff[n - 1][i][0] = sff[n - 1][i][1] = a[n - 1][i];
}
for(int i = 0; i < n; i++){
up[i][0] = a[i][0];
upp[i][0][0] = upp[i][0][1] = a[i][0];
dw[i][m - 1] = a[i][m - 1];
dww[i][m - 1][0] = dww[i][m - 1][1] = a[i][m - 1];
}
for(int i = 1; i < n; i++){
for(int j = 0; j < m; j++){
prr[i][j][0] = prr[i][j][1] = a[i][j];
if(j - 1 >= 0){
prr[i][j][0] += prr[i - 1][j - 1][0];
}
if(j + 1 < m){
prr[i][j][1] += prr[i - 1][j + 1][1];
}
pr[i][j] = pr[i - 1][j] + prr[i][j][0] + prr[i][j][1] - a[i][j];
}
}
for(int i = n - 2; i > -1; i--){
for(int j = 0; j < m; j++){
sff[i][j][0] = sff[i][j][1] = a[i][j];
if(j - 1 >= 0){
sff[i][j][0] += sff[i + 1][j - 1][0];
}
if(j + 1 < m){
sff[i][j][1] += sff[i + 1][j + 1][1];
}
sf[i][j] = sf[i + 1][j] + sff[i][j][0] + sff[i][j][1] - a[i][j];
}
}
for(int j = 1; j < m; j++){
for(int i = 0; i < n; i++){
upp[i][j][0] = upp[i][j][1] = a[i][j];
if(i - 1 >= 0){
upp[i][j][0] += upp[i - 1][j - 1][0];
}
if(i + 1 < n){
upp[i][j][1] += upp[i + 1][j - 1][1];
}
up[i][j] = up[i][j - 1] + upp[i][j][0] + upp[i][j][1] - a[i][j];
}
}
for(int j = m - 2; j > -1; j--){
for(int i = 0; i < n; i++){
dww[i][j][0] = dww[i][j][1] = a[i][j];
if(i - 1 >= 0){
dww[i][j][0] += dww[i - 1][j + 1][0];
}
if(i + 1 < n){
dww[i][j][1] += dww[i + 1][j + 1][1];
}
dw[i][j] = dw[i][j + 1] + dww[i][j][0] + dww[i][j][1] - a[i][j];
}
}
}
void solve(vector<int> a[], vector<int> b[], int n, int m){
vector<int> pr[n], sf[n], up[n], dw[n];
for(int i = 0; i < n; i++){
pr[i].resize(m, 0);
sf[i].resize(m, 0);
up[i].resize(m, 0);
dw[i].resize(m, 0);
}
cal(a, pr, sf, up, dw, n, m);
b[0][0] = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(a[i][j]){
b[0][0] += max(i, j);
}
}
}
for(int i = 1; i < m; i++){
b[0][i] = b[0][i - 1] + up[0][i - 1] - dw[0][i];
}
for(int i = 1; i < n; i++){
for(int j = 0; j < m; j++){
b[i][j] = b[i - 1][j] + pr[i - 1][j] - sf[i][j];
}
}
}
int32_t main() {
int t;
cin>>t;
while(t--){
int n, m;
cin>>n>>m;
vector<int> a[n], b[n], ar[n], br[n];
for(int i = 0; i < n; i++){
a[i].resize(m, 0);
b[i].resize(m, 0);
ar[i].resize(m, 0);
br[i].resize(m, 0);
}
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
int temp;
cin>>temp;
if(temp == 1 || temp == 3){
a[i][j] = 1;
}
if(temp == 2 || temp == 3){
b[i][j] = 1;
}
}
}
solve(a, ar, n, m);
solve(b, br, n, m);
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cout<<abs(ar[i][j] - br[i][j])<<" ";
}
cout<<"\n";
}
}
}