PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author & Editorialist: Alei Reyes
Tester: Shubham Jain, Aryan Choudhary
DIFFICULTY:
Hard
PREREQUISITES:
median-graphs
PROBLEM:
You are given the edges of a triangle free circle graph.
There is one city in each face of the planar graph, and K of them are special. You can move from one city to another if their respective regions share an edge.
A city is good, if minimizes the sum of distances to each of the K special cities.
In one query you can choose two cities x, y, and the interactor gives you the number of special cities closer to x than y and the number of special cities closer than y to x.
Find all the good cities (medial set).
QUICK EXPLANATION:
Construct the faces from the edges (dual graph). The dual is a median graph, use the majority strategy to find the holy ciites, similar to finding the centroid of a tree
EXPLANATION:
1. Construct the dual
Finding the faces of a general planar graph can be difficult. However our graph is special, each internal vertex has at most degree 4 (because no 3 segments intersect at the same point). Moreover, we are already given the vertices of the unbounded face: the points 1 \ldots 2 \cdot N on the circumference.
Let’s keep a list of the open faces of the graph in clockwise order. Initially the open faces are (1,2), (2,3), \ldots (2 \cdot N, 1). In each step of the algorithm we’ll find one face, ore merge two open faces.
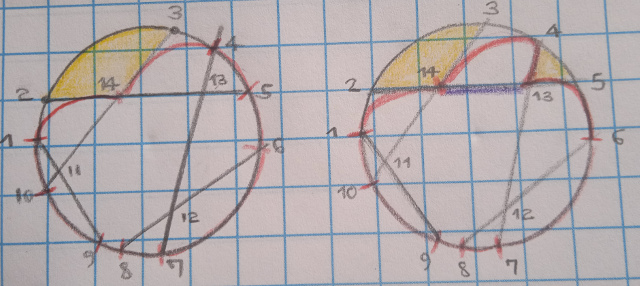
Let f=(x_1, x_2, ..., x_l) be an open face, there are three cases:
- There is one vertex u that joins the two endoints of f
If there exists a vertex u and edges (x_1,u), (u, x_l), then f is closed and two new open faces (x_1, u), (u,x_l) are created.
In the figure of the left, the face (2,3) is closed and a new region (2,3,14) is discovered.
- There is one edge that connects the two endpoints of f
If there exists an edge (x_1,x_l) in the graph, then f is closed, and a new open face (x_1, x_l) is created.
In the figure of the right, the open face (14,3,4,13) is closed by the edge (14,13).
- Two adjacent paths are merged
Whenever one of the endpoints of an open face doesn’t have an outgoing edge, it can be merged with their adjacent open face.
For example, in the figure of the left, after adding the edges (2,14) and (14,3), we can merge the paths (1,2), (2,14), similarly the paths (14,3) and (3,4)
2. Find the medial set
When the graph is a tree, if there are two special vertices u and v, then the medial set is the path connecting those vertices, because if we move one step away from u then we get one step closer to v keeping the sum of distances equal to the length of the path. When there are more special vertices, we can use a similar majority strategy:
- Start from a vertex u, if there is an edge (u,v) in the graph and at least half of the special cities are closer to v than u, then v is at least as good as u, so we can start again our search starting from v.
If we repeat the previous step without visiting the same vertex twice, we’ll end up in a good vertex x. Then we can start a bfs from x and visit each vertex y that is as good as x. Each vertex is visited at most once, therefore the number of used queries is at most equal to the number of faces.
It turns out that the resulting dual graph of our triangle-free circle graph is a median graph, and the majority strategy also works! Can you prove it?
About SHRINES
Sorry for the long long statement, initially I planned to directly give the dual in the input, however when generating test data I noticed it was kind of interesting to find the faces. After I defined the internal intersection points, and how the cities are numbered it became too long.