PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Contest Division 4
Setter: Aruj Bansal
Tester: Harris Leung
Editorialist: Aman Dwivedi
DIFFICULTY:
Easy-Medium
PREREQUISITES:
DP, Segment Tree/Fenwick Tree
PROBLEM:
You are given a N×M matrix A, filled with distinct numbers. You can start at any cell. If you are currently at cell (x_1,y_1), then you can jump to any other cell (x_2,y_2), if and only if the following two conditions are satisfied:
- A_{x_2,y_2}>A_{x_1,y_1}
- Manhattan distance between A_{x_2,y_2} and A_{x_1,y_1} > S.
Let V be the set of the cells visited by you.
Maximize the value of \sum_{(x,y)∈V} A_{x,y}.
EXPLANATION:
Let’s process the cells in the increasing order of the values. Hence, now we need to find the maximum values in the cell which have been processed and which has a manhattan distance greater than S from the cell where we are standing.
We can solve it by Dynamic Programming. Let’s define our DP as:
-
DP(x,y) is defined as the maximum value that we can achieve when all the cells whose value is less than A_{x,y} have been processed.
-
Transition of DP will be as we saw above i.e:
where maximum is the maximum value in the cell which have been processed and which has a manhattan distance greater than S from the cell where we are standing.
If we iterate over all the cells to find which cells are valid, then it will require O((N*M)^2) complexity which is too high to pass the constraints. Can we do better? Let’s see:
Let’s consider the given matrix in the four kinds of diagonals.
- All Diagonals that start from the top-left corner.
- All Diagonals start from the top-right corner.
- All Diagonals start from the bottom-left corner.
- All Diagonals start from the bottom-right corner.
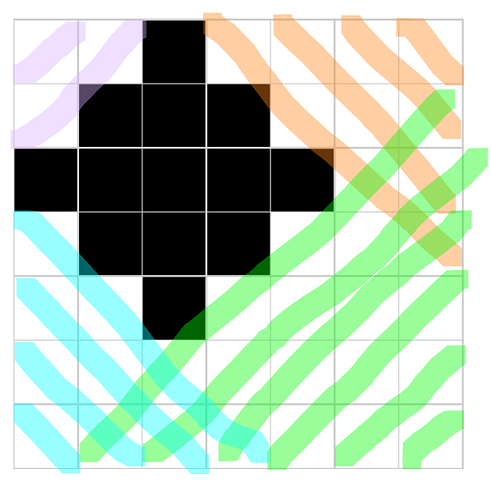
Suppose we are at cell (x,y). Now all the cells whose Manhattan Distance is less than or equal to S from the cell (x,y) form a diamond. Credits to czhang2718 for the image below.
As we can see in the figure, there are 4 types of diagonal which are defined above. Now in order to optimize the above DP let’s make a segment tree or Fenwick tree for all four types of diagonal. You can create Fenwick Trees in such a way that the starting index in the tree is the first cell from where the diagonal begins.
Now, instead of traversing all the cells, we can simply find the maximum prefix in all the four types of Fenwick trees we created. Finally, we can update the value of the cell in all of the $4$trees. Hence now our transition of DP will be as follows:
where T_1, T_2, T_3, T_4 are the Fenwick trees that we created.
This helps in reducing the time for transitions from O(N*M) to O(4*log(N+M)).
Our answer will be the maximum value that we find in the DP.
TIME COMPLEXITY:
O(N*M * log(N+M)) per test case
SOLUTIONS:
Setter's Solution
#ifdef DEBUG
#define _GLIBCXX_DEBUG
#endif
//#pragma GCC optimize("O3")
#include <bits/stdc++.h>
using namespace std;
typedef long double ld;
typedef long long ll;
int n, m, s;
const ll INF = 1e18;
struct Fenwick{
int n;
vector<ll> f;
Fenwick(int _n) {
n = _n;
f = vector<ll>(n + 1, -INF);
}
ll get(int r) {
ll ans = 0;
while (r > 0) {
ans = max(ans, f[r]);
r &= (r - 1);
}
return ans;
}
void upd(int v, ll by) {
while (v <= n) {
f[v] = max(f[v], by);
v = (v | (v - 1)) + 1;
}
}
};
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
// freopen("input.txt", "r", stdin);
int tst;
cin >> tst;
while (tst--) {
cin >> n >> m >> s;
vector<vector<ll>> a(n + 1, vector<ll>(m + 1));
vector<pair<int, pair<int, int>>> tt;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
tt.emplace_back(make_pair(a[i][j], make_pair(i, j)));
}
}
sort(tt.begin(), tt.end());
Fenwick difA(n + m);
Fenwick difB(n + m);
Fenwick sumA(n + m);
Fenwick sumB(n + m);
ll he = 0;
for (auto &it : tt) {
int x = it.second.first;
int y = it.second.second;
ll best = 0;
best = max(best, difA.get(x - y + m - s - 1));
best = max(best, difB.get(y - x + n - s - 1));
best = max(best, sumA.get(x + y - s - 1));
best = max(best, sumB.get(n + m + 1 - x - y - s - 1));
best += it.first;
he = max(he, best);
difA.upd(x - y + m, best);
difB.upd(y - x + n, best);
sumA.upd(x + y, best);
sumB.upd(n + m + 1 - x - y, best);
}
cout << he << '\n';
}
return 0;
}
Tester's Solution
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fi first
#define se second
const ll mod=998244353;
int t;
int n,m,s;
ll mx[2][262144];
void upd(int t,int id,int l,int r,int p,ll v){
if(l==r){
mx[t][id]=max(mx[t][id],v);
return;
}
int mid=(l+r)/2;
if(p<=mid) upd(t,id*2,l,mid,p,v);
else upd(t,id*2+1,mid+1,r,p,v);
mx[t][id]=max(mx[t][id*2],mx[t][id*2+1]);
}
ll qry(int t,int id,int l,int r,int ql,int qr){
if(l>qr || r<ql) return 0;
if(ql<=l && r<=qr) return mx[t][id];
int mid=(l+r)/2;
return max(qry(t,id*2,l,mid,ql,qr),qry(t,id*2+1,mid+1,r,ql,qr));
}
void build(int id,int l,int r){
mx[0][id]=mx[1][id]=0;
if(l==r) return;
int mid=(l+r)/2;
build(id*2,l,mid);
build(id*2+1,mid+1,r);
}
pair<ll,pair<int,int> >a[1000001];
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int t;cin >> t;
while(t--){
cin >> n >> m >> s;s++;
for(int i=1; i<=n ;i++){
for(int j=1; j<=m ;j++){
ll x;cin >> x;
a[(i-1)*m+j]={x,{i,j}};
}
}
sort(a+1,a+n*m+1);
build(1,1,n+m-1);
ll ans=0;
for(int i=1; i<=n*m ;i++){
int x=a[i].se.fi;
int y=a[i].se.se;
ll best=0;
if(x+m-y+s<=n+m-1) best=max(best,qry(0,1,1,n+m-1,x+m-y+s,n+m-1));
if(x+m-y-s>=1) best=max(best,qry(0,1,1,n+m-1,1,x+m-y-s));
if(x+y-1+s<=n+m-1) best=max(best,qry(1,1,1,n+m-1,x+y-1+s,n+m-1));
if(x+y-1-s>=1) best=max(best,qry(1,1,1,n+m-1,1,x+y-1-s));
best+=a[i].fi;
ans=max(ans,best);
upd(0,1,1,n+m-1,x+m-y,best);
upd(1,1,1,n+m-1,x+y-1,best);
}
cout << ans << '\n';
}
}