Do you know how to prove your solution?
PROBLEM LINK:
Author: Sahil Chimnani
Tester: Radoslav Dimitrov
Editorialist: William Lin
DIFFICULTY:
Cakewalk
PREREQUISITES:
Greedy, Basic Geometry
PROBLEM:
There are N widths and N heights. You need to form N rectangles, such that each width and each height is assigned to a rectangle. For each rectangle, draw a circle of maximum area which can be inscribed in that rectangle. Find the maximum sum of diameters of the N circles.
QUICK EXPLANATION:
The maximum diameter of a circle that can be inscribed in a w by h rectangle is min(w, h). Sort the widths and the heights. Greedily pair the first width with the first height, second with with the second height, and so on.
EXPLANATION:
Let the sequence A be the widths of the rectangles and the sequence B be the heights of the rectangles.
The first thing we should do is to find a formula for the maximum diameter of a circle in terms of the side lengths of the rectangle. Then, we are able to calculate the final answer, if we already know how to pair up the widths and the heights.
Observation 1. Maximum diameter of a circle that can be inscribed in a w by h rectangle is min(w, h).
Explanation
We can figure this out by drawing a few simple diagrams:
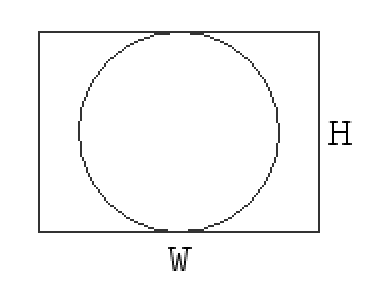
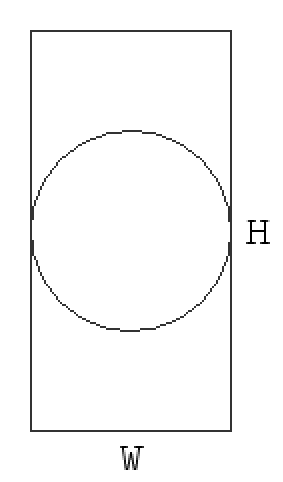
Now that we know the formula, let’s rephrase the problem a bit: Given the sequences A and B, we can reorder their elements in any way that we want. Find the maximum possible value of \sum_{i = 1}^{N} min(A_i, B_i).
How should we pair the elements of A and B? Note that if we pair big element with a small element, the big element is, in some way, “wasted”, since the value of the pair is minimum.
For example, consider A=[5, 3] and B=[2, 4].
If we don’t reorder the sequences, 5 is paired with 2, and 3 is paired with 4, which gives a total value of min(5, 2)+min(3, 4)=5.
If we choose to pair the 3 with the 2 instead, we can use the 5 for the 4, which gives a total value of min(3, 2)+min(5, 4)=6.
Following from this intuition, it seems like we want to pair the small elements with the small elements, middle elements with the middle elements, and the big elements with the big elements, in order to maximize the final sum. This leads to the following observation:
Observation 2. It is optimal to reorder both sequences by sorting them.
Proof
We can prove this by induction on N, the length of the sequences.
When N=1, there is only one possible way to reorder both sequences, so sorting them works.
When N=k, consider the minimum element of both sequences, A_{min} and B_{min}. Without loss of generality, A_{min} \le B_{min}. What element of B should we pair A_{min} with? It turns out that it doesn’t matter! Since all elements of B are greater than or equal to A_{min}, the value of the pair will always be A_{min}.
Since the element of B we choose to pair with A_{min} doesn’t affect the value of the pair, we should use B_{min} in order to maximize the value of other pairs.
So, we concluded that pairing A_{min} with B_{min} is optimal.
What about the other k-1 elements of both sequences? By our induction hypothesis, sorting the k-1 elements of both sequences is optimal.
By sorting all k elements, we will both pair A_{min} and B_{min} while making the other k-1 elements of both sequences sorted, so sorting the k elements is indeed optimal.
To conclude, we will first sort A and B, then find \sum_{i = 1}^{N} min(A_i, B_i).
HIDDEN TRAPS
- The maximum possible answer can be up to N \cdot 10^9 = 10^{13}, which exceeds the range of 32-bit integers (like int in C++ and Java). Make sure to use 64-bit integers (like long long in C++ & and long in Java)!
- N can be up to 10^4, so make sure to use a fast O(N \log N) sorting algorithm (most langauges provide such an implementation in their standard library, like sort() in C++ and Arrays.sort in Java). O(N^2) sorting algorithms like selection sort should not pass.
SOLUTIONS:
Setter's Solution
for _ in range(int(input())):
n=int(input())
l1=sorted(list(map(int,input().split())))
l2=sorted(list(map(int,input().split())))
lfin=[]
ll=list(zip(l1,l2))
for i in range(n):
lfin+=[min(ll[i])]
print(sum(lfin))
Tester's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (int)1e4 + 42;
int n;
int a[MAXN], b[MAXN];
void read() {
cin >> n;
for(int i = 0; i < n; i++) {
cin >> a[i];
}
for(int i = 0; i < n; i++) {
cin >> b[i];
}
}
void solve() {
int64_t answer = 0;
vector<pair<int, int> > li;
for(int i = 0; i < n; i++) {
li.pb({a[i], 0});
li.pb({b[i], 1});
}
sort(li.rbegin(), li.rend());
vector<int> av = {0, 0};
for(auto it: li) {
if(av[it.second ^ 1]) {
av[it.second ^ 1]--;
answer += it.first;
} else {
av[it.second]++;
}
}
cout << answer << endl;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int T;
cin >> T;
while(T--) {
read();
solve();
}
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mxN=1e4;
int n, a[mxN], b[mxN];
void solve() {
//input
cin >> n;
for(int i=0; i<n; ++i)
cin >> a[i];
for(int i=0; i<n; ++i)
cin >> b[i];
//sort the arrays
sort(a, a+n);
sort(b, b+n);
ll ans=0;
//pair a[i] with b[i] for each i
for(int i=0; i<n; ++i) {
//diameter is min(a[i], b[i])
ans+=min(a[i], b[i]);
}
//output
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()