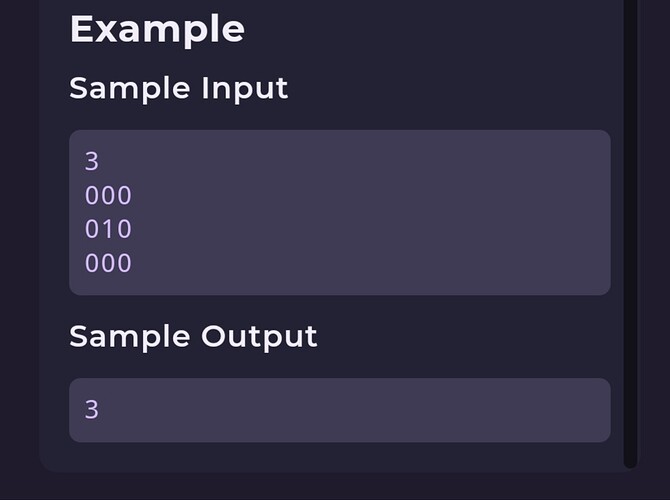
Apply BFS on given matrix.
-
If you found a ‘0’ and it is not visited, give a BFS call to it and visit all the '0’s which are connected to it (horizontally, vertically and diagonally also).
-
Store the co-ordinates of that ‘0’ which is farthest from the position from where you make this call. Let’s say, it’s position is (x, y), then convert all the '0’s to '1’s in the square sub-matrix having its corners as starting position to (max(x, y), max(x, y))
-
Calculate the length and add this to the answer.
-
Repeat this process for all the cells of the matrix.
For eg:
4x4 matrix
0 1 1 0
1 0 0 1
1 1 1 1
1 1 1 1
- As (0,0) cell has ‘0’, make a bfs call and visit all the '0’s connected to it like (1,1), (1, 2), (0, 3) .
- As the farthest ‘0’ is found in (0, 3), so the max(0, 3) is 3.
From (0, 0) to (0+3, 0+3) , for this square sub-matrix, convert all '0’s to '1’s.
Resultant Matrix:
1 1 1 1 // sq. sub-matrix started at (0,0)
1 1 1 1
1 1 1 1 // and ended at pos(3,3) //converted all '0's to '1's in this sub-matrix
1 1 1 1
Answer = 4 (as the length is 3+1)
I am not sure whether this approach is correct or not, but looking at the constraints, I think this approach would work.
Got it… Thank you