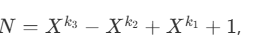PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author:
Tester: apoorv_me
Editorialist: iceknight1093
DIFFICULTY:
Easy - Medium
PREREQUISITES:
None
PROBLEM:
An even number N is called X-valid if the integers from 1 to N can be partitioned into \frac N 2 pairs, each of which has a sum that is a power of X.
Given N and X, count the X-valid numbers between 1 and N.
EXPLANATION:
As a first step, let’s analyze when exactly N can be X-valid.
N itself must be paired with something to reach a sum that’s a power of X.
Let X^k be the smallest power of X that exceeds N.
Note that if X = 1 such a power doesn’t exist so N certainly cannot be X-valid. For any X \geq 2, a valid power does always exist.
Then, observe that N must be paired with X^k - N. This is because it’s impossible to reach any larger power: the next larger power is X^{k+1} = X\cdot X^k \geq 2X^k, while the maximum possible sum at all is 2N - 1 \lt 2X^k.
So, let’s define f_X(N) to be the unique element that must be paired with N.
Note that if f_X(N) \geq N then N definitely isn’t X-good; so we only need to care about f_X(N) \lt N.
Since N and f_X(N) are paired up, we can certainly also pair up N-1 with f_X(N)+1, N-2 with f_X(N)+2, and so on.
In fact, this is the only valid pairing for these numbers.
Why?
Let y be the smallest integer such that N-y is not paired with f_X(N) + y.
Since they aren’t paired, and everything larger than (N-y) is already paired, N-y must be paired with something strictly smaller than it to reach a power of X.
This power of X that’s reached can’t be X^k, so it has to be something smaller: in particular, it must be \leq N (and yet \gt N-y).But we know that all the numbers from N-y+1 to N are already paired with something smaller than them to sum to X^k.
This means we have a power of X that, when summed with something smaller than it, reaches a higher power of X. For X \geq 2, this is impossible.So, such a y cannot exist, meaning all the values in [f_X(N), N] must pair among themselves to reach a sum of X^k.
In particular, since all the numbers in the interval [f_X(N), N] must be paired within themselves, this interval must have even length: meaning N and f_X(N) have different parities.
However, X^k = N + f_X(N) is then an odd number, meaning X must itself be odd.
This immediately tells us that if X is even, there are no X-valid numbers.
We only deal with the case when X is odd now.
Observe that with everything in the range [f_X(N), N] paired up already, we only have all the integers \leq f_X(N) - 1 remaining.
If f_X(N) = 1 then we’re done since everything is paired up; otherwise N is X-valid only if f_X(N) - 1 is itself X-valid.
So, for N to be X-valid, the sequence N, f_X(N) - 1, f_X(f_X(N) - 1)-1, \ldots must be strictly decreasing, and has to terminate in 0.
Let’s try to figure out what this means for N in terms of X.
First, if f_X(N) - 1 = 0, that means N+1 is a power of X, i.e, N = X^k - 1.
Next, suppose f_X(f_X(N) - 1) - 1 = 0.
This means f_X(N) is itself a power of X, say X^{k_1}; and reaches another power of X, say X^{k_2}, when added to N.
So, N = X^{k_2} - X^{k_1}, where k_2 \gt k_1 \gt 0.
For the next level, if we have f_X(N)-1 = X^{k_2} - X^{k_1}, then we’ll have N = X^{k_3} - X^{k_2} + X^{k_1} - 1, where k_3 \gt k_3 \gt k_1 \gt 0.
It’s not hard to see that this pattern continues: N will look like the alternating sum of descending powers of X, with an additional -1 if the number of powers is odd.
There is, in fact, a rather simple classification of such numbers: they’re exactly those integers whose base-X representations contain only the digits 0 and (X-1).
This should be relatively easy to see: simply follow how the base-X representation changes as you add and subtract decreasing powers of X.
We now know that if X is even, there are no X-valid numbers, and when X is odd, the only X-valid numbers are those whose digits in base X are either 0 or (X-1).
So, when X is even the answer is 0, and when X is odd we simply need to count the number of integers \leq N which contain only 0's and (X-1)'s in their base X representations.
The latter is not very hard to do: fix the prefix of N (in base X) that matches with the number, then make the next digit 0 (since if we’re to fall strictly below N, any valid number must have the digit 0), and then all following digits can be freely chosen as either 0 or X-1, for 2^k choices if there are k free digits.
Of course, if the matching prefix ever contains some digit other than 0 or (X-1), break out immediately.
This takes \mathcal{O}(\log_X N) time, since we only compute the base-X representation of N and iterate through its digits once.
TIME COMPLEXITY:
\mathcal{O}(\log N) per testcase.
CODE:
Author's code (C++)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INF (int)1e18
mt19937_64 RNG(chrono::steady_clock::now().time_since_epoch().count());
void Solve()
{
int n, x; cin >> n >> x;
if (x % 2 == 0){
cout << 0 << "\n";
return;
}
if (x == 1){
cout << 0 << "\n";
return;
}
// numbers can be 0 or x - 1 in base x
vector <int> a;
// generate base x representation of n
while (n > 0){
a.push_back(n % x);
n -= (n % x);
n /= x;
}
reverse(a.begin(), a.end());
int ans = 0;
// answer by fixing prefix of a, then smaller
for (int i = 0; i < (int)a.size(); i++){
if (a[i] == 0) continue;
// equal till i - 1, smaller afterwards
// forced to have a[i] = 0
// edge case when all 0?
int v = 1;
for (int j = i + 1; j < (int)a.size(); j++){
v *= 2;
}
ans += v;
if (a[i] != x - 1 && a[i] != 0) break;
}
bool good = true;
for (auto y : a){
good &= (y == 0) || (y == x - 1);
}
if (good) ans++;
ans--;
cout << ans << "\n";
}
int32_t main()
{
auto begin = std::chrono::high_resolution_clock::now();
ios_base::sync_with_stdio(0);
cin.tie(0);
int t = 1;
// freopen("in", "r", stdin);
// freopen("out", "w", stdout);
cin >> t;
for(int i = 1; i <= t; i++)
{
//cout << "Case #" << i << ": ";
Solve();
}
auto end = std::chrono::high_resolution_clock::now();
auto elapsed = std::chrono::duration_cast<std::chrono::nanoseconds>(end - begin);
cerr << "Time measured: " << elapsed.count() * 1e-9 << " seconds.\n";
return 0;
}
Editorialist's code (PyPy3)
for _ in range(int(input())):
n, x = map(int, input().split())
if x%2 == 0 or x == 1:
print(0)
continue
digits = []
while n > 0:
digits.append(n % x)
n //= x
digits = digits[::-1]
ans = 0
for i in range(len(digits)):
if digits[i] == 0: continue
ans += 2 ** (len(digits) - i - 1)
if digits[i] != x-1: break
ans -= 1
if digits.count(0) + digits.count(x-1) == len(digits): ans += 1
print(ans)