PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Shubham Jain and Jyothi Surya Prakash Bugatha
Tester: Aryan Choudhary
Editorialist: Taranpreet Singh
DIFFICULTY
Easy-Medium
PREREQUISITES
Divide and Conquer, Interactive problems, Centroid of a tree.
PROBLEM
There is a tree consisting of N nodes. A certain node X is marked as special, but you don’t know X - your task is to find it. To achieve this, you can ask queries to obtain information about X.
To be specific, you can ask queries in the form:
? Y
where 1 \le Y \le N, and you will be provided with a random node on the path from node Y to node X, excluding Y. If Y = X you will receive -1 instead.
You can ask at most 12 queries. Find the special node X.
QUICK EXPLANATION
- At each step, query for the centroid of the tree. This way, the response to the query shall always be a subtree half the size of the original tree.
- When you query a node q and receive a response v, you only need to consider the subtree which contains the response node v.
- To identify which subtree node v belongs to, you can run BFS or DFS. We can ignore the rest of the tree.
EXPLANATION
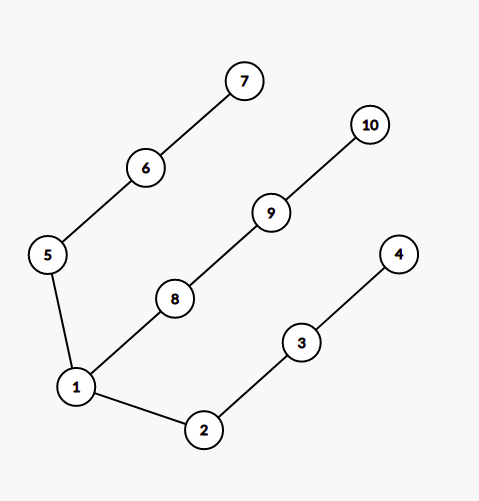
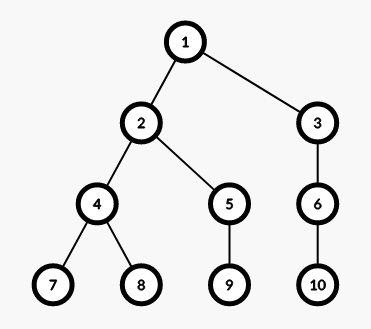
We’ll consider the following tree throughout the editorial
Let’s assume we query at node 1.
- If the hidden node is 1, the case is solved.
- If the hidden node is among [2,3,4], we’d get a node from [2,3,4] in response.
- If the hidden node is among [5,6,7], we’d get a node from [5,6,7] in response.
- If the hidden node is among [8,9,10], we’d get a node from [8,9,10] in response.
Hence, based on the response, we are able to reduce the possible candidates for X from 10 to 3.
Let’s assume we query at node 8 instead of 1.
- If the hidden node is 8, the case is solved.
- If the hidden node is among [9, 10], we’d get a node from [9,10] in response.
- If the hidden node is among [1,2,3,4,5,6,7], we’d get a node from [1,2,3,4,5,6,7] response.
In this case, assuming the worst, we are able to reduce the possible number of candidates from 10 to 7 (happens when the response is 1 for querying node 8).
So, it is better to query node 1 here as compared to 8.
Observation
We want to query at a node such that the size of the largest subtree of its child, is minimized. For node 1, it had 3 children of size 3 each, while node 8 had two children, one of size 2 and one of subtree size 7.
Claim: It is always possible to reduce the number of candidates by at least half in each query.
Anyone, who has used centroid decomposition even once would immediately know that centroid of a tree is a node such that no subtree of this node has a size greater than the size of the original tree.
Hence, for each query, we shall query the centroid of the remaining tree, find the subtree to which the response node belongs, and discard the rest of the tree.
For example, if when queried node 1, if we receive node 7 in response, we only need to keep tree consisting of nodes [5,6,7].
Why doesn’t this exceed 12 queries?
At each query, the number of candidates reduces by at least half. At the start, there are N candidates. At the end, in order to solve the problem, there must be only one candidate left.
Hence, the number of queries must be the smallest integer x such that \displaystyle \left \lfloor \frac{N}{2^x}\right \rfloor \leq 1 which implies N \leq 2^x \implies x \geq log_2(N).
For N \leq 1000, this translates to roughly 10 or 11 queries. depending upon implementation.
TIME COMPLEXITY
The time complexity is O(N*log(N)) or O(N^2) depending upon implementation.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
vector<int> g[N];
int sz[N], dead[N];
void dfs_sz(int v, int p){
if(dead[v]){
sz[v] = 0;
return;
}
sz[v] = 1;
for(int u : g[v]){
if(u == p)continue;
dfs_sz(u, v); sz[v] += sz[u];
}
}
int query(int v){
cout << "? " << v << endl;
int x; cin >> x; return x;
}
void dfs(int v){
dfs_sz(v, 0);
int bg = -1;
for(int u : g[v]){
if(bg == -1 || sz[u] > sz[bg]){
bg = u;
}
}
if(bg == -1){
assert(query(v));
cout << "! " << v << endl;
return;
}else if(sz[bg] <= sz[v]/2){
int u = query(v);
if(u == -1){
cout << "! " << v << endl;
return;
}
dead[v] = true;
dfs(u);
}else{
dfs(bg);
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while(t--){
int n;
cin >> n;
for(int i = 1; i <= n; i++){
g[i].clear();
dead[i] = 0;
}
for(int i = 2; i <= n; i++){
int u, v;
cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
dfs(1);
}
return 0;
}
Tester's Solution
/* in the name of Anton */
/*
Compete against Yourself.
Author - Aryan (@aryanc403)
Atcoder library - https://atcoder.github.io/ac-library/production/document_en/
*/
#ifdef ARYANC403
#include <header.h>
#else
#pragma GCC optimize ("Ofast")
#pragma GCC target ("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx")
//#pragma GCC optimize ("-ffloat-store")
#include<bits/stdc++.h>
#define dbg(args...) 42;
#endif
// y_combinator from @neal template https://codeforces.com/contest/1553/submission/123849801
// http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2016/p0200r0.html
template<class Fun> class y_combinator_result {
Fun fun_;
public:
template<class T> explicit y_combinator_result(T &&fun): fun_(std::forward<T>(fun)) {}
template<class ...Args> decltype(auto) operator()(Args &&...args) { return fun_(std::ref(*this), std::forward<Args>(args)...); }
};
template<class Fun> decltype(auto) y_combinator(Fun &&fun) { return y_combinator_result<std::decay_t<Fun>>(std::forward<Fun>(fun)); }
using namespace std;
#define fo(i,n) for(i=0;i<(n);++i)
#define repA(i,j,n) for(i=(j);i<=(n);++i)
#define repD(i,j,n) for(i=(j);i>=(n);--i)
#define all(x) begin(x), end(x)
#define sz(x) ((lli)(x).size())
#define pb push_back
#define mp make_pair
#define X first
#define Y second
// #define endl "\n"
typedef long long int lli;
typedef long double mytype;
typedef pair<lli,lli> ii;
typedef vector<ii> vii;
typedef vector<lli> vi;
const auto start_time = std::chrono::high_resolution_clock::now();
void aryanc403()
{
#ifdef ARYANC403
auto end_time = std::chrono::high_resolution_clock::now();
std::chrono::duration<double> diff = end_time-start_time;
cerr<<"Time Taken : "<<diff.count()<<"\n";
#endif
}
long long readInt(long long l, long long r, char endd) {
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true) {
char g=getchar();
if(g=='-') {
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g&&g<='9') {
x*=10;
x+=g-'0';
if(cnt==0) {
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd) {
if(is_neg) {
x=-x;
}
assert(l<=x&&x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret="";
int cnt=0;
while(true) {
char g=getchar();
assert(g!=-1);
if(g==endd) {
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt&&cnt<=r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l,r,' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l,r,'\n');
}
string readStringLn(int l, int r) {
return readString(l,r,'\n');
}
string readStringSp(int l, int r) {
return readString(l,r,' ');
}
void readEOF(){
assert(getchar()==EOF);
}
vi readVectorInt(int n,lli l,lli r){
vi a(n);
for(int i=0;i<n-1;++i)
a[i]=readIntSp(l,r);
a[n-1]=readIntLn(l,r);
return a;
}
#include <algorithm>
#include <cassert>
#include <vector>
namespace atcoder {
struct dsu {
public:
dsu() : _n(0) {}
explicit dsu(int n) : _n(n), parent_or_size(n, -1) {}
int merge(int a, int b) {
assert(0 <= a && a < _n);
assert(0 <= b && b < _n);
int x = leader(a), y = leader(b);
if (x == y) return x;
if (-parent_or_size[x] < -parent_or_size[y]) std::swap(x, y);
parent_or_size[x] += parent_or_size[y];
parent_or_size[y] = x;
return x;
}
bool same(int a, int b) {
assert(0 <= a && a < _n);
assert(0 <= b && b < _n);
return leader(a) == leader(b);
}
int leader(int a) {
assert(0 <= a && a < _n);
if (parent_or_size[a] < 0) return a;
return parent_or_size[a] = leader(parent_or_size[a]);
}
int size(int a) {
assert(0 <= a && a < _n);
return -parent_or_size[leader(a)];
}
std::vector<std::vector<int>> groups() {
std::vector<int> leader_buf(_n), group_size(_n);
for (int i = 0; i < _n; i++) {
leader_buf[i] = leader(i);
group_size[leader_buf[i]]++;
}
std::vector<std::vector<int>> result(_n);
for (int i = 0; i < _n; i++) {
result[i].reserve(group_size[i]);
}
for (int i = 0; i < _n; i++) {
result[leader_buf[i]].push_back(i);
}
result.erase(
std::remove_if(result.begin(), result.end(),
[&](const std::vector<int>& v) { return v.empty(); }),
result.end());
return result;
}
private:
int _n;
std::vector<int> parent_or_size;
};
} // namespace atcoder
vector<vi> readTree(const int n){
vector<vi> e(n);
atcoder::dsu d(n);
for(lli i=1;i<n;++i){
const lli u=readIntSp(1,n)-1;
const lli v=readIntLn(1,n)-1;
e[u].pb(v);
e[v].pb(u);
d.merge(u,v);
}
assert(d.size(0)==n);
return e;
}
const lli INF = 0xFFFFFFFFFFFFFFFL;
lli seed;
mt19937 rng(seed=chrono::steady_clock::now().time_since_epoch().count());
inline lli rnd(lli l=0,lli r=INF)
{return uniform_int_distribution<lli>(l,r)(rng);}
class CMP
{public:
bool operator()(ii a , ii b) //For min priority_queue .
{ return ! ( a.X < b.X || ( a.X==b.X && a.Y <= b.Y )); }};
void add( map<lli,lli> &m, lli x,lli cnt=1)
{
auto jt=m.find(x);
if(jt==m.end()) m.insert({x,cnt});
else jt->Y+=cnt;
}
void del( map<lli,lli> &m, lli x,lli cnt=1)
{
auto jt=m.find(x);
if(jt->Y<=cnt) m.erase(jt);
else jt->Y-=cnt;
}
bool cmp(const ii &a,const ii &b)
{
return a.X<b.X||(a.X==b.X&&a.Y<b.Y);
}
const lli mod = 1000000007L;
// const lli maxN = 1000000007L;
lli T,n,i,j,k,in,cnt,l,r,u,v,x,y;
lli m;
string s;
vi a;
//priority_queue < ii , vector < ii > , CMP > pq;// min priority_queue .
int main(void) {
ios_base::sync_with_stdio(false);cin.tie(NULL);
// freopen("txt.in", "r", stdin);
// freopen("txt.out", "w", stdout);
// cout<<std::fixed<<std::setprecision(35);
T=readIntLn(1,10);
while(T--)
{
const int n=readIntLn(1,1e3);
const auto e=readTree(n);
vector<bool> vis(n,false);
vi size(n,0);
auto dfs1=y_combinator([&](const auto &self,lli u,lli p)->lli{
size[u]=1;
for(auto x:e[u])
{
if(x==p||vis[x])
continue;
size[u]+=self(x,u);
}
return size[u];
});
auto search=[&](lli u,lli totalActive,lli p)
{
while(true)
{
lli best=0;
lli bigger=u;
for(auto x:e[u])
{
if(x==p||vis[x])
continue;
if(best<size[x])
{
best=size[x];
bigger=x;
}
}
if(best<=totalActive/2)
return u;
p=u;
u=bigger;
}
};
auto getCentroid=[&](lli start)
{
lli totalActive=dfs1(start,-1);
return search(start,totalActive,-1);
};
auto getNode=[&](int u){
return getCentroid(u);
};
u=0;
while(true){
u=getNode(u);
cout<<"? "<<u+1<<endl;
cin>>v;
if(v==-1)
break;
vis[u]=true;
u=v-1;
}
cout<<"! "<<u+1<<endl;
} aryanc403();
// readEOF();
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class SPCNODE{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni();qc = 0;
int[] from = new int[N-1], to = new int[N-1];
for(int i = 0; i< N-1; i++){
from[i] = ni()-1;
to[i] = ni()-1;
}
int[][] tree = make(N, N-1, from, to, true);
boolean[] cmarked = new boolean[N];
int start = 0;
while(true){
int[] size = new int[N], par = new int[N];
Arrays.fill(par, -1);
dfs(tree, size, par, cmarked, start, -1);
int centroid = centroid(tree, size, cmarked, start, -1, size[start]);
int q = query(centroid);
if(q == -2){
answer(centroid);
break;
}
cmarked[centroid] = true;
dfs(tree, size, par, cmarked, centroid, -1);
while(par[q] != centroid)q = par[q];
start = q;
}
}
void dfs(int[][] tree, int[] size, int[] par, boolean[] cmarked, int u, int p){
par[u] = p;
for(int v:tree[u]){
if(v == p || cmarked[v])continue;
dfs(tree, size, par, cmarked, v, u);
size[u] += size[v];
}
size[u]++;
}
int centroid(int[][] tree, int[] size, boolean[] cmarked, int u, int p, int total){
for(int v:tree[u]){
if(v == p || cmarked[v])continue;
if(size[v]*2 > total)
return centroid(tree, size, cmarked, v, u, total);
}
return u;
}
int qc = 0;
int query(int x) throws Exception{
hold(++qc <= 12);
pni("? "+(1+x));
return ni()-1;
}
void answer(int x) throws Exception{
pni("! "+(1+x));
}
int[][] make(int n, int e, int[] from, int[] to, boolean f){
int[][] g = new int[n][];int[]cnt = new int[n];
for(int i = 0; i< e; i++){
cnt[from[i]]++;
if(f)cnt[to[i]]++;
}
for(int i = 0; i< n; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< e; i++){
g[from[i]][--cnt[from[i]]] = to[i];
if(f)g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new SPCNODE().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()