PROBLEM LINK
Author : Vikesh Tiwari
Editorialist: Vikesh Tiwari
DIFFICULTY
medium-hard
PREREQUISITES
data structures,maths, number theory
PROBLEM
Chef has list of all Fibonacci Numbers but in modulo 1013. This list in infinite.
We know that Fibonacci sequence starts with 0 and 1. So in this list each number apart from first two, is sum of previous two numbers modulo 1013.
ex : (a+b)mod 1013.
So beginning of the list looks like : 0, 1, 1, 2, 3, 5, 8, 13, 21, …
Now you’re given an integer n, find first occurrence of n in the given list. (0-indexed)
EXPLANATION
Main idea: baby-step-giant-step.
In this problem we had some Fibonacci number modulo 1013, and we had to determine the position of its first occurence in Fibonacci sequence modulo 1013.
- Let a and b be two different coprime modula — divisors of 1013.
- Let F be the actual Fibonacci number such that
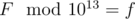 . Then
. Then 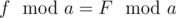 and
and 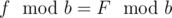 .
. - Find all occurences of number
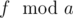 in Fibonacci sequence modulo a period.
in Fibonacci sequence modulo a period. - Find all occurences of number
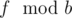 in Fibonacci sequence modulo bperiod.
in Fibonacci sequence modulo bperiod. - Let's fix a pair of such occurences. Let the occurence modulo a be in position i, and the occurence modulo b be in position j.
- Let t(m)be Fibonacci sequence modulom period.
- From the Chinese Remainder Theorem, it follows that t(ab) = LCM(t(a), t(b)) (remember that a and b are coprime).
- Then from fixed occurences of f in periods of sequences modulo a and b we can recover the position of occurence of f in period of sequence modulo ab. It could be done by solving the following Diophantine equation: i + t(a) * x = j + t(b) * y. We can solve it using a simple bruteforce of one of the roots.
- If the occurence in sequence modulo ab period ( we have just found it) is u, then every occurence f in Fibonacci sequence modulo 1013 period can be represented as t(ab) * k + u. Then let's bruteforce k and find all occurences in sequence modulo 1013 period. To determine Fibonacci number on position α + t(ab) from known Fibonacci number on position α, we need to multiply the vector (Fα, Fα + 1) and some matrix.
- Let's choose a = 59 and b = 213. Note that there is no number that occur Fibonacci sequence modulo a or b period more than 8 times. That means that total count of pairs will never be greater than 64. For each occurence we'll bruteforce not more than
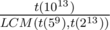 numbers. That was the author's solution.
numbers. That was the author's solution.
Also that was possible to use the fact that for any number the count of its occurences in period of sequence modulo <span tex-span">10<sup upper-index">p (for any natural <span tex-span">p) is not big more efficiently. From occurences in sequence modulo <span tex-span">10<sup upper-index">i period we could get occurences in sequence modulo <span tex-span">10<sup upper-index">i + 1 period using the method we use to jump from modulus <span tex-span">ab to modulus <span tex-span">10<sup upper-index">13.
C++ Code
//Strange Fibonacci
//Fibonacci Using Matrix
#include<cstdio>
#include<cstring>
typedef long long ll;
ll mod,ans[1000],res[1000];
ll mul(ll a,ll b){
return b==0?0:((mul(a,b>>16)<<16)+a*(b&(1<<16)-1))%mod;
}
void mul(ll f[2][2],ll g[2][2]){
ll a[2][2];
a[0][0]=(mul(f[0][0],g[0][0])+mul(f[0][1],g[1][0]))%mod;
a[0][1]=(mul(f[0][0],g[0][1])+mul(f[0][1],g[1][1]))%mod;
a[1][0]=(mul(f[1][0],g[0][0])+mul(f[1][1],g[1][0]))%mod;
a[1][1]=(mul(f[1][0],g[0][1])+mul(f[1][1],g[1][1]))%mod;
memcpy(f,a,sizeof a);
}
void init(ll g[2][2]){
g[0][0]=g[1][1]=1,g[0][1]=g[1][0]=0;
}
void quick(ll f[2][2],ll n){
ll g[2][2];
for (init(g);n;n>>=1){
if (n&1) mul(g,f);
mul(f,f);
}
memcpy(f,g,sizeof g);
}
void init1(ll f[2][2]){
f[0][0]=0,f[0][1]=f[1][0]=f[1][1]=1;
}
bool dw(ll g[2][2]){
return g[0][0]==1 && g[1][1]==1 && !g[0][1] && !g[1][0];
}
int main(){
ll n,tm;
ll f[2][2],g[2][2],h[2][2];
int i,j,k,cnt,pp;
scanf("%lld",&n);
for (mod=tm=1,cnt=1,ans[0]=0,i=0;i<13;i++){
mod=mod*10;
init1(f);
quick(f,tm);
init(g),pp=0,j=0;
do{
for (k=0;k<cnt;k++){
init1(h);
quick(h,ans[k]+tm*j);
if (h[1][0]==n%mod) res[pp++]=ans[k]+tm*j;
}
mul(g,f);
j++;
} while (!dw(g));
memcpy(ans,res,sizeof res);
cnt=pp;
tm*=j;
}
printf("%lld\n",cnt==0?-1:ans[0]);
return 0;
}