I have been trying to understand the solution of [GSS1][1] problem from last 2 days but still not been able to get why are we maintaining the suffixsum and prefixsum of every node. here is the link to the
[2]. can you please explain me the code from line 36 to 48. i have already searched a lot on google but still not been able to get it. please help.
[1]: http://www.spoj.com/problems/GSS1/
[2]: http://ideone.com/UgPrJTCode Gyan This is a blog by ayur jain, It is well explained and better to understand what is happening in the code.
In GSS1, few of the things you need to consider are best left sum, best right sum, best sum and sum - code by ayur jain Qq25J5 - Online C++ Compiler & Debugging Tool - Ideone.com
PS i solved this problem after going through his editorial
Here’s another similar question regarding GSS1 problem : Please Check the solution to SPOJ GSS1 problem. - general - CodeChef Discuss
You might look into the code here : https://github.com/Shraeyas/SPOJ-Solutions/blob/master/gss1.cpp
Codechef: Crazy Malvika discovers Crazy Fibonacci function
Asking questions on a new thread without enough karma is impermissible here, so I can’t. Please look into the question.
I read the CHN08 - Editorial, but I still can’t understand enough of it.
@anno In an array prefix sum comes from left subtree and suffix sum comes from right subtree, therefore to calculate the best sum we need store max(max(A.best,B.best),A.suffix+B.prefix)
Go through the image I’ve calculated what is actually happening in code
We take tree[n].prefix=max(tree[2n+1].prefix,tree[2n+1].sum+B.prefix) because max sum can be in left sub tree or left subtree + left subtree of right sub tree and vice versa for tree[n] suffix
This pic is just to depict the meaning, you can paper run the program on these values to better understand the codes.
Can somebody tell why I am getting WA?
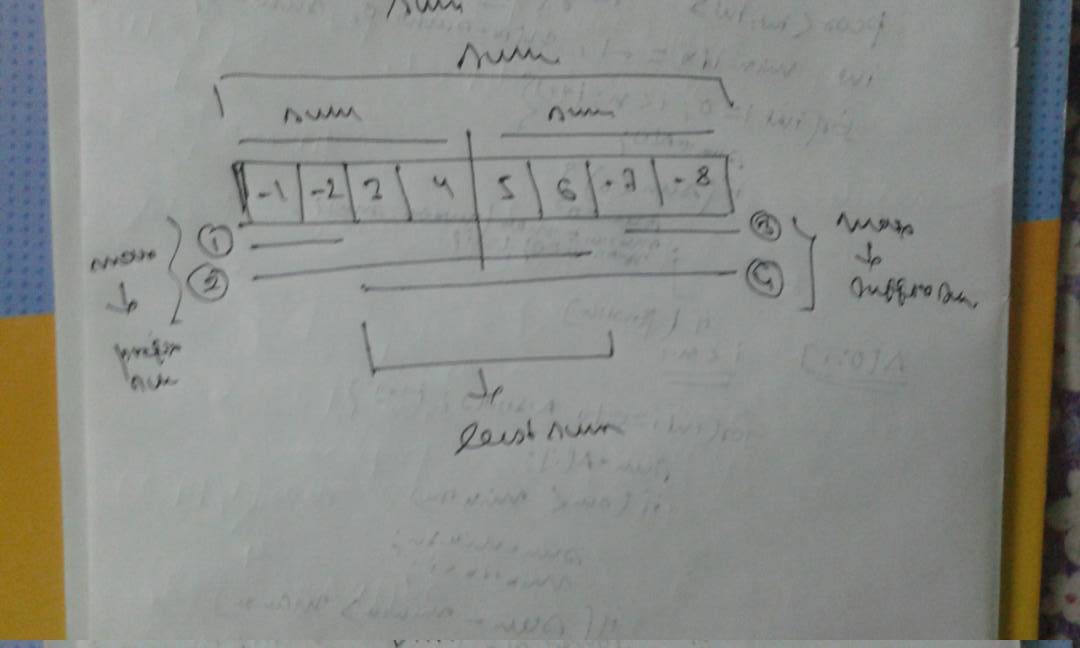
Here’s my attempt at explaining the approach. The problem is the maximum sum subarray problem, which you want to solve by a divide and conquer approach, which is what a segment tree does.
For a given range A, you split it into two pieces, the left half L and the right half R. Naturally the maximum sum subarray in A can lie either 1) completely in L, or lie 2) completely in R, or 3) cross over from L to R. Solve recursively for the two halves. We get the maximum sum subarrays for the left half as L.maxsum and the right half as R.maxsum, and now we know the first 2 of the 3 options just like that *snaps fingers* 
How do we get the third option? A range that extends from L to R can be broken into a suffix of L and a prefix of R. So if we know the maximum suffix sum in L as L.suffixsum and the maximum prefix sum in R as R.prefixsum, the sum of those 2 values will give us the maximum sum subarray extending from L to R, which covers option 3. So we get
tree[index].maxsum = max(max(tree[2\*index+1].maxsum, tree[2\*index+2].maxsum),
tree[2\*index+1].suffixsum + tree[2\*index+2].prefixsum);
Now since we have incorporated 2 new values (prefixsum and suffixsum), the parent range of A will also require these from A. So now we need to calculate A.prefixsum and A.suffixsum. The maximum sum prefix of A can be 1) the maximum sum prefix of L, or 2) cover the whole of L and extend into R. Option 1 is simply L.prefixsum, and option 2 is \sum L + R.prefixsum. Similarly, the maximum sum suffix of A is either R.suffixsum or \sum R + L.suffixsum. So now it seems we need another value to represent a range, which is the sum of that range. So we have
tree[index].prefixsum = max(tree[2\*index+1].prefixsum,
tree[2\*index+1].sum + tree[2\*index+2].prefixsum);
tree[index].suffixsum = max(tree[2\*index+2].suffixsum,
tree[2\*index+2].sum + tree[2\*index+1].suffixsum);
And for the sum it is simply
tree[index].sum = tree[2\*index+1].sum + tree[2\*index+2].sum;
Well, that covers the whole thing, I hope it is clear why we require the 4 values in one node of the segment tree. Also you can see that the calculation of tree[index].maxsum in the link you provided can be simplified as I have described above. Feel free to ask if anything is not clear 
Here’s the accepted code : kUy1h1 - Online C++ Compiler & Debugging Tool - Ideone.com
Simply changed those vectors to array and added cin.tie(0) for fast IO.
@meooow @neilit1992 for the ans of any query we are checking if (l > mid) or if (r <= mid) why are we doing this
int mid = (start+end)/2;
if (l > mid)
return query(2*index+2, mid+1, end, l, r);
if (r <= mid)
return query(2*index+1, start, mid, l, r);
node left = query(2*index+1,start,mid,l,r);
node right = query(2*index+2,mid+1,end,l,r);@anno you can have a look on this video tutorial to clear your doubts regarding Segment Trees.
Here’s the Link
Now as far as your question is concerned,
l and r are the intervals in which we have to make query on the segment tree.
Also start to mid and mid+1 to end are the two segments in which we have divided the current interval(i.e. start to end). Now start to mid will be in the left child of current node and mid+1 to end will be in the right child of current node.
Now it should be clear that in your code if l>mid, then we don’t have to query on the left child of current node, that’s why we simply moved to position 2*pos+2 (right child).
Similarly, if r<=mid then we can straightaway move to the left child of current node, that is why you did set the position there to 2*pos+1
Hope this helps. If you have any other doubts please comment below. 
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
ll arr[50005];
struct Tree{
ll pre,su,tot,bst;
}tree[200005];
void build_tree(ll node,ll a,ll b)
{
if(a==b)
{
tree[node].pre=arr[a];
tree[node].su=arr[a];
tree[node].tot=arr[a];
tree[node].bst=arr[a];
return;
}
ll mid=(a+b)>>1;
build_tree(node2,a,mid);
build_tree(node2+1,mid+1,b);
tree[node].pre=max(tree[node2].pre,tree[node2].tot+tree[node2+1].pre);
tree[node].su=max(tree[node2+1].su,tree[node2+1].tot+tree[node2].su);
tree[node].tot=tree[node2].tot+tree[node2+1].tot;
tree[node].bst=max(tree[node2].su+tree[node2+1].pre,max(tree[node2].bst,tree[node2+1].bst));
}
Tree query_tree(ll node, ll a ,ll b, ll i,ll j)
{
Tree t;
if(a>b||a>j||b<i)
{
t.pre=t.su=t.bst=INT_MIN;
t.tot=0;
return t;
}
if(a>=i&&b<=j)
return tree[node];
ll mid=(a+b)>>1;
Tree q1=query_tree(node2,a,mid,i,j);
Tree q2=query_tree(node2+1,mid+1,b,i,j);
t.pre=max(q1.pre,q1.tot+q2.pre);
t.su=max(q2.su,q2.tot+q1.su);
t.tot=q1.tot+q2.tot;
t.bst=max(q1.su+q2.pre,max(q1.bst,q2.bst));
return t;
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>arr[i];
build_tree(1,1,n);
ll q;
cin>>q;
while(q–)
{
ll l,r;
cin>>l>>r;
Tree a=query_tree(1,1,n,l,r);
cout<<a.bst<<"\n";
}
}
Can you please explain me concept of prefixsum and sufixsum for every node?? Means why and how are we maintaining those two sums
Delete this post and ask in a new thread now.
@anno I’ve uploaded pics, prefix sum is max of ( (sum of left subtree + left node sum of right subtree) and left node sum of left subtree)
suffix sum is max of (( sum of right subtree+right node sum of left subtree) and right node sum of right sub tree)
It’s just the normal approach but iterative instead of recursive.
It is failing for this case
10
-1 9 2 6 -4 3 5 2 -6 1
1
4 7
The answer should be 8 while your code gives 6.