Encountered this rather interesting problem on Combinatorial Game Theory, no threads were present on this theorem so I thought I’ll create one.
INTRODUCTION
What is Sprague-Grundy Theorem?
Suppose there is a Composite game being played among two players say A and B with let’s say N subgames. The Sprague-Grundy Theorem says that if both A and B play optimally then the player starting first is guaranteed to win if the XOR of the Grundy Numbers of position in each sub-game at the beginning of the game is non-zero. Otherwise, if XOR evaluates to zero, then definitely the player not making the start will win.
I will only be discussing the application to keep thread short and simple and not the proof, refer this for proof.
What are Grundy Numbers?
Grundy Numbers are used to define the state of the game, and these are calculated at the initial condition of each sub-game.
Mathematically: The Grundy Number/ nimber is equal to 0 for a game that is lost immediately by the first player, and is equal to Mex of the nimbers of all possible next positions for any other game.
Calculation of mex
‘Minimum excludant’ a.k.a ‘Mex’ of a set of numbers is the smallest non-negative number not present in the set.
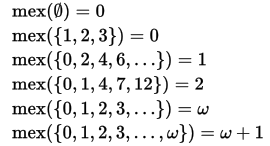
CALCULATIONS
To solve the problem as a whole, we analyse all sub-games individually and arrive at a result by XORing results of individual sub-games which can be known by analysing the grundy number for that sub-game. So our problem breaks down to create a function which can generate grundy numbers for a subgame.
Consider the following example for clarification:
EXAMPLE
The game starts with a pile of n stones, and the player to move may take any positive number of stones upto 3 only. The last player to move wins. Which player wins the game? This game is 1 pile version of Nim.
Since if the first player has 0 stones, he will lose immediately, so Grundy(0) = 0
If a player has 1 stones, then he can take all the stones and win. So the next possible position of the game (for the other player) is (0) stones
Hence, Grundy(1) = Mex(0) = 1 [According to the definition of Mex]
Similarly, if a player has 2 stones, then he can take only 1 stone or he can take 2 stones and win. So the next possible position of the game (for the other player) is (1, 0) stones respectively.
Hence, Grundy(2) = Mex(0, 1) = 2 [According to the definition of Mex]
Similarly, Grundy(3) = Mex(0, 1, 2) = 3 [According to the definition of Mex]
But what about 4 stones ?
If a player has 4 stones, then he can take 1 stone or he can take 2 stones or 3 stones, but he can’t take 4 stones (see the constraints of the game). So the next possible position of the game (for the other player) is (3, 2, 1) stones respectively.
Hence, Grundy(4) = Mex (1, 2, 3) = 0 [According to the definition of Mex]
So we can define Grundy Number of any n >= 4 recursively as-
Grundy(n) = Mex[Grundy (n-1), Grundy (n-2), Grundy (n-3)]
We summarize the first the Grundy Value from 0 to 10 in the below table-

NOTE: The function to calculate grundey number will be depending on the problem.
Function in this case:
int calculateGrundy(int n){
if (n == 0)
return (0);
if (n == 1)
return (1);
if (n == 2)
return (2);
if (n == 3)
return (3);
unordered_set<int> Set; // A Hash Table
for (i from 1 to 3)
Set.insert(calculateGrundy(n - i));
return (calculateMex(Set));
}
Refer this pseudo-code for the calculation of Mex about which we talked earlier:
calculateMex(unordered_set a)
Mex = 0
while(a.find(Mex)!=a.end())
return Mex
It is advised to either pre-calculate grundy numbers and store in array/vector for fast access or calculate grundy number for each sub-game depending on the constraints
Now we’re in a stage where we have grundy numbers calculated, so using Sprague-Grundy Theorem, take XOR of all grundy numbes from all sub-games.
If NON-ZERO - The player who started wins else the player who plays second wins and that gives us our winner.
Any questions, suggestions/improvements are most welcome.
Thanks to @vijju123 for linking me to the source of this.
Sources: geeksforgeeks