PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter:
Tester & Editorialist: Taranpreet Singh
DIFFICULTY
Easy
PREREQUISITES
Binary Lifting, LCA.
PROBLEM
Given a tree with N nodes, among with K nodes are marked as special. You are also given a node A. For each node B, determine the maximum value of d(A, X)-d(B, X) where d(a, b) denotes the number of edges on unique path from a to b, and X is any special node. Also, find one X node which maximizes d(A, X)-d(B, X) for each B.
QUICK EXPLANATION
- Rooting the tree at node A. For node B, it is optimum to choose X such that the depth of LCA(X, B) is maximized.
- It is equivalent to finding the deepest ancestor P of node B such that subtree of P contains atleast 1 special node. Maximum value of d(A, X)-d(B, X) = d(A, P)-d(B, P)
EXPLANATION
Let’s consider the following tree with A = 1 and consider B = 10, and special nodes are 5, 6 and 9.
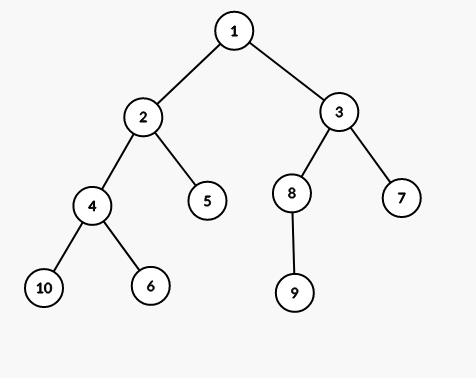
Following images depict d(A, X) and d(B, X) by red and purple path respectively.
With X = 6
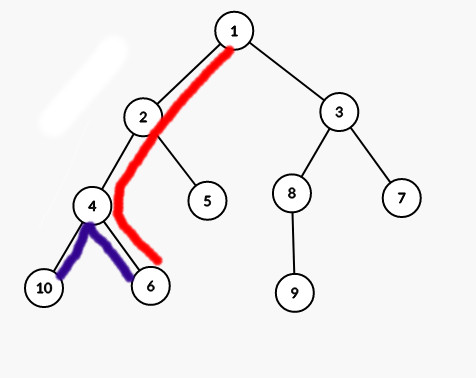
With X = 5
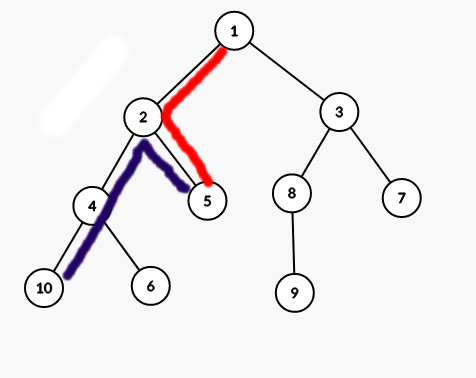
With X = 9
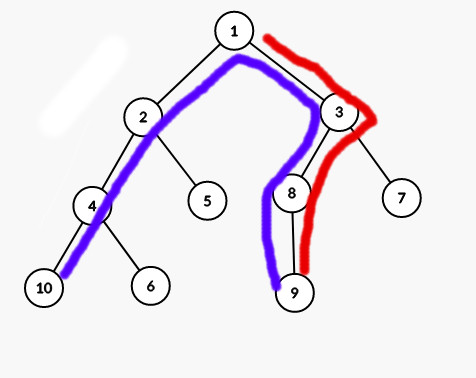
What we are looking for is the maximum value of d(A, X)-d(B, X).
These paths have common path d(L, X) for each X where L is the first common vertex on the path from A to X and path B to X.
If we root the tree on A, the first common vertex L is by definition the Lowest Common Ancestor of B and X.
Now, In order to maximize d(A, X)-d(B, X) = d(A, L)-d(B, L) where L lies on path from A to B, we can see that we need to maximize d(A, L) and minimize d(B, L) which implies we should select L closest to B such that there exists some special node X corresponding to such L.
Restating, for a fixed B, we are looking for the lowest ancestor L of B such that subtree of L contains at least one special node.
If you have managed to follow till here, you have solved the hard part of the problem. All that is left is implementation here.
Let’s assume for each node u, we have computed sp(u) which returns any special descendent in subtree of node u or -1 if there’s no special node in subtree of node u.
Naive way would be to consider each node B one by one and keep moving to its parent till sp(u) \neq -1.
One way to optimize is to notice the fact that if we consider all nodes on path from A to B in the order they appear, some non-prefix of nodes shall have sp(u) \neq -1 and remaining suffix (possibly empty) of nodes in this list shall have sp(u) = -1. We need to find the last node having sp(u) \neq -1.
Hence, we can use binary lifting to find the lowest ansestor of node B.
Bonus
It is possible to solve this problem in O(N) too.
How?
Run a dfs to find sp(u) for each node u and another dfs passing the deepest node x on path from root to current node having sp(x) \neq -1 shall work. Implementation is left as an exercize.
TIME COMPLEXITY
The time complexity of binary lifting solution is O(N*log(N)) per test case.
SOLUTIONS
Setter's Solution O(N)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5+45;
int n,k,a;
int spc[N];
vector <int> g[N];
int has[N];
int dep[N],closest[N],spnode[N];
void prep(int x,int par){
has[x] |= spc[x];
int spn = 0;
for(auto f : g[x]){
if(f == par) continue;
dep[f] = dep[x]+1;
prep(f,x);
has[x] |= has[f];
if(has[f]) spn = spnode[f];
}
if(spc[x]) spnode[x] = x;
else spnode[x] = spn;
}
void dfs(int x,int par){
if(has[x]) closest[x] = x;
else closest[x] = closest[par];
for(auto f : g[x]){
if(f == par) continue;
dfs(f,x);
}
}
void solve(){
cin >> n >> k >> a;
for(int i = 1; i <= n; i++){
g[i].clear();
spc[i] = dep[i] = closest[i] = has[i] = spnode[i] = 0;
}
for(int i = 1; i <= k; i++){
int x;
cin >> x;
spc[x] = 1;
}
for(int i = 1; i < n; i++){
int u,v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dep[a] = 0;
prep(a,0);
dfs(a,0);
for(int i = 1; i <= n; i++){
int maxval = 2*dep[closest[i]]-dep[i];
cout << maxval;
if(i < n) cout << " ";
else cout << endl;
}
for(int i = 1; i <= n; i++){
cout << spnode[closest[i]];
if(i < n) cout << " ";
else cout << endl;
}
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--){
solve();
}
}
Tester's Solution
import java.util.*;
import java.io.*;
class SPTREE{
//SOLUTION BEGIN
int B = 18;
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), K = ni(), root = ni()-1;
boolean[] special = new boolean[N];
for(int i = 0; i< K; i++)special[ni()-1] = true;
int[] from = new int[N-1], to = new int[N-1];
for(int i = 0; i< N-1; i++){
from[i] = ni()-1;
to[i] = ni()-1;
}
int[][] tree = make(N, N-1, from, to, true);
int[] depth = new int[N];
int[][] par = new int[B][N];
for(int b = 0; b< B; b++)Arrays.fill(par[b], -1);
int[] specialDescendent = new int[N];
Arrays.fill(specialDescendent, -1);
dfs(tree, par, depth, special, specialDescendent, root, -1);
int[] ans = new int[N];
Arrays.fill(ans, Integer.MIN_VALUE);
int[] node = new int[N];
Arrays.fill(node, -1);
for(int u = 0; u< N; u++){
int cur = u;
for(int b = B-1; b >= 0; b--)
if(par[b][cur] != -1 && specialDescendent[par[b][cur]] == -1)
cur = par[b][cur];
if(specialDescendent[cur] == -1)cur = par[0][cur];
node[u] = specialDescendent[cur];
ans[u] = 2*depth[cur]-depth[u];
}
StringBuilder o = new StringBuilder();
for(int x:ans)o.append(x+" ");
o.append("\n");
for(int x:node)o.append((1+x)+" ");
pn(o.toString());
}
void dfs(int[][] tree, int[][] par, int[] d, boolean[] special, int[] specialDescendent, int u, int p){
for(int b = 1; b< B; b++)
if(par[b-1][u] != -1)
par[b][u] = par[b-1][par[b-1][u]];
if(special[u])specialDescendent[u] = u;
for(int v:tree[u])
if(v != p){
d[v] = d[u]+1;
par[0][v] = u;
dfs(tree, par, d, special, specialDescendent, v, u);
if(specialDescendent[u] == -1)specialDescendent[u] = specialDescendent[v];
}
}
int[][] make(int n, int e, int[] from, int[] to, boolean f){
int[][] g = new int[n][];int[]cnt = new int[n];
for(int i = 0; i< e; i++){
cnt[from[i]]++;
if(f)cnt[to[i]]++;
}
for(int i = 0; i< n; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< e; i++){
g[from[i]][--cnt[from[i]]] = to[i];
if(f)g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
// new SPTREE().run();
new Thread(null, new Runnable() {public void run(){try{new SPTREE().run();}catch(Exception e){e.printStackTrace();System.exit(1);}}}, "1", 1 << 28).start();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()


