PROBLEM LINK:
Author: Milos Puric
Tester: Aryan Choudhary
Editorialist: Srikkanth R
DIFFICULTY:
Medium
PREREQUISITES:
Segment Trees, LCA queries on Trees
PROBLEM:
You are given a tree with N nodes and Q queries of the following types
-
1 uMark the node u as special -
2 uMark the node u as not special -
3 KDetermine whether there exists a node in the tree (not necessarily special) whose maximum distance to one of the special nodes is exactlyK
For each query of type 3, print 0 if the answer is false and 1 otherwise. Initially none of the nodes are marked as special.
QUICK EXPLANATION:
Firstly we build a data structure to compute \texttt{dist}(u, v) between any two given vertices in O(1) time.
For every query of type 3, it is sufficient to consider only the pair of special nodes that are farthest apart in the tree and the end points of the diameter of the tree. If one of these distances between the four pairs of points is at least K and K is at least \frac{\texttt{dist}(u, v)}{2} then the answer is true, otherwise the answer is false.
To include queries 1 and 2, we need to be able to find the pair of special nodes that are farthest apart quickly and with updates. To do these operations, we can maintain a segment tree, where in each node of the segment tree that has interval [L, R] we store the only the pair of special nodes in the interval [L, R] that are farthest apart.
For merging it is sufficient to consider the farthest pair from each of the pairs of special nodes computed in the children. There are only O(1) such pairs, so merging can be done in O(1).
EXPLANATION:
Queries of type 3
We first look at how to answer operations of type 3 quickly and worry about updates later.
Let’s first setup the tree for answering LCA and distance queries between pairs of nodes in O(1) time.
Fast LCA Queries
We first build the Euler Tour of the input tree.
Then the LCA of two nodes u and v can be obtained by looking at the interval [L, R] in the Euler Tour of the tree where L is the first occurrence of node u and R is the first occurrence of node v. (Here assume that u occurs first in the Euler Tour, otherwise we can just swap the nodes). The node which has the lowest depth in the interval [L, R] is the LCA of the two nodes u, v.
Now it is sufficient to find build an interval range minimum query data strucutre on the Euler Tour of the tree. If we use sparse tables, we can get a constant query time.
For more details refer this blog.
The total preprocessing time is O(N \log N) and query time for LCA is O(1). The preprocessing can even be reduced to O(N) but we need not bother with that optimisation since the constant factors are large anyway.
The distance between two vertices \texttt{dist}(u, v) can then be calculated as \texttt{depth}(u) + \texttt{depth}(v) - 2 * \texttt{depth}(\texttt{lca}(u, v)), which also takes O(1) time.
Starting with the most naive solution, let’s find the maximum distance from each node in the tree to any of the special nodes by the following brute force algorithm (we use \texttt{maxDist}(n) to denote the distance of the farthest special node to node n):
maxDist := An array of size n, initialised to -1
for each node u from 1 to n:
for each node v that is marked special:
maxDist[u] := max(maxDist[u], dist(u, v))
Since the distance queries are O(1), the above code takes O(n^2) time, since there could be O(n) special nodes, however we can show that we need to consider only certain O(1) special nodes.
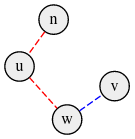
For example suppose w is a special node that lies on the path between two other special nodes u, v (see diagram below), then any path ending at w can be extended to one of u, v yielding a higher distance. Therefore we can ignore such special nodes while performing the second iteration in the brute force, since they never contribute to the answer.
We can extend this idea to see that we need to only consider two special nodes. You should try to find them yourself before reading Observation 1.
Observation 1. Suppose u, v are two special nodes such that D_s = \texttt{dist}(u, v) is maximum among all pairs of special nodes, then for all nodes n in the tree \texttt{maxDist}(n) = \max(\texttt{dist}(n, u), \texttt{dist}(n, v))
Proof
Let u, v be the special nodes with maximum distance between them, and let w be any other special node.
It will be helpful to think of the tree in the manner shown below.
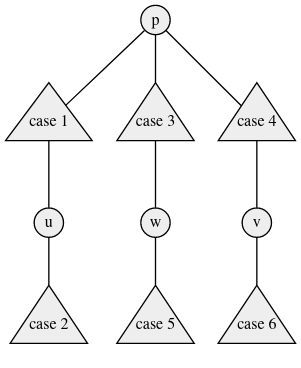
In the diagram node p is the closest node to w that lies on \texttt{path(u, v)}. The triangles represent sub-trees. The diagram can be thought of as a general representation of any tree.
In the preceding paragraphs, we already saw the case when w lies on the path between u, v. Notice that here we have assumed that that is not the case. Also since by u, v is the farthest set of special nodes, w cannot lie in case 6 or case 2 (why?). In other words we can assume that p is always different from u, v, w since the other cases are easy to deal with.
We will now argue that given any node n, wherever it occurs in the tree, one of u, v are always farther from n than w.
Note that :
- \texttt{dist}(u, v) = \texttt{dist}(u, p) + \texttt{dist}(v, p)
- \texttt{dist}(w, v) = \texttt{dist}(w, p) + \texttt{dist}(v, p)
- \texttt{dist}(w, u) = \texttt{dist}(w, p) + \texttt{dist}(u, p)
Using \texttt{dist}(u, v) \geq \texttt{dist}(u, w) and \texttt{dist}(u, v) \geq \texttt{dist}(v, w)
we get that \texttt{dist}(p, w) is the shortest among \texttt{dist}(p, u), \texttt{dist}(p, v). This fact will be useful for us.
-
Case 1: \texttt{dist}(p, v) \geq \texttt{dist}(p, w) so if n lies in these sub-trees, v is farther than (or the same distance as) w.
-
Case 2: By assumption, passing through u and then to v gives the maximum distance
-
Case 3: This is the most tricky case. Consider the last common point between \texttt{path}(n, w) and \texttt{path}(n, v), i.e. the point from which the path to v and w from n starts diverging. Let this point be m. Upto m, the path is identical and the distances are same. After m, the maximum possible distance to w is \texttt{dist}(p, w), and the minimum possible distance to v is \texttt{dist}(p, v). Thus v is farther than w.
-
Cases 4 & 6: Same as cases 1 & 2, but with u, v swapped, so the same arguments follow.
We can see that irrespective of where the node n lies, one of u, v is always farther when compared to w, as desired.
From observation 1, it is clear that to answer the query, we need to determine if there exists a node n such that \max(\texttt{dist}(n, u), \texttt{dist}(n, v)) = K. however the following observations and case work will help us consider each of the nodes separately.
Observation 2. There is no solution if K \le \frac{D_s}{2}
Proof
Observe that at least one of the paths from \texttt{path}(n, u), \texttt{path}(n, v) contain either the left half or the right half of \texttt{path}(u, v) completely. Therefore \texttt{maxDist}(n) \geq \frac{D_s}{2}, so if K < \frac{D_s}{2} it is not possible for \texttt{maxDist}(n) to equal K.
Observation 3. There is always a solution if \frac{D_s}{2} \leq K \leq D_s
Proof
Refer the diagram in observation 2. p_K is the desired node. Note that p_D = v.
Observation 4. If K > D_s then it is sufficient to find any node that has a distance of at least K from one of the two special nodes u, v computed above.
Proof
Suppose the farthest special node from n is u and has a length of at least K. We can shrink the path to size K by removing nodes at the other end of the node u. Since K \geq \frac{D_s}{2}, the path we’ve obtained must contain at least one half of \texttt{path}(u, v) and so u still remains as the farthest point from n and this completes the construction.
Now it is sufficient to find the farthest node from u and v. Similar to observation 1, we can show that it is sufficient to consider only the endpoints of the diameter of the tree to find the farthest node from each of u, v. The following generalisation of Observation 1, will be useful.
Observation 5. Suppose S and T are two subsets of nodes in the tree. Then for each node in s, the maximum of distance of s to any node t belonging to T is equal to one of \texttt{dist}(s, T_u), \texttt{dist}(s, T_v), where \texttt{dist}(T_u, T_v) is maximum among pairs of nodes belonging to T.
Note that observation 1 is as special case of observation 5 with T = the set of special nodes and S = the set of all nodes in the tree.
Now consider S = \{u, v\}, and T = set of all nodes in the tree. Suppose T_u, T_v are the end points of the diameter of the tree (i.e \texttt{dist}(T_u, T_v) is maximum among all pairs of nodes in the tree), then from the above Observation 5, the maximum distance from u is one of \texttt{dist}(u, T_u), \texttt{dist}(u, T_v) and similarly for node v. If any one of the four pairs of distances are greater than K, then by observation 4 the answer for our query is true.
Revisiting the brute force algorithm, we see that we can replace the first for loop, with just the endpoints of the diameter and the inner for loop with the two special nodes u, v and then compute the maximum of all desired pairs of nodes in O(1).
Now we can answer every query of type 3 in O(1) time.
Queries 1 & 2
We need to find a way to compute the farthest special points, when the set of special points are updated by either addition or deletion of a node. We can do this by using a segment tree.
[details=Segment Tree Implementation Details]
Consider a segment tree where in each node [L, R] we store the pair of special nodes which are farthest apart among all pairs of special nodes such that both of them lie in the range [L, R].
Let’s consider an internal node of the segment tree corresponding to an interval [L, R] with left child l and right child r, and M = \lfloor \frac{L + R}{2}\rfloor.
Using Observation 5 with S = the set of special nodes in the left child and T = the set of special nodes in the right child we find that it is sufficient to look only at the farthest pairs of nodes among the nodes stored in the left and right children. There are at most 4 nodes and \binom{4}{2} = 6 pairs to consider. So merging elements in the segment tree can be done in O(1) by computing the distances for each pair and choosing the one that is maximum.
Therefore we can use the usual segment tree with updates. This gives a total of O(\log N) time to support each operation of type 1 and 2.
Finally note that if a segment tree node does not contain any special nodes, we can have a pair of dummy invalid nodes which always give a distance of -1 (or any invalid distance). For more details refer the source code below.
[\details]
COMPLEXITY:
TIME: \mathcal{O}((N + Q) \log N)
SPACE: \mathcal{O}(N \log N)
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+23;
int n,q;
int typ[N],param[N],frst[N],spec[N];
int ans[N];
vector <int> g[N];
int up[N][20]; /// up to 17 is enough
int dep[N],depval[2*N][20],spdep[2*N][20],logs[2*N];
int tin[N],tout[N],what[2*N],clk = 1;
int ind = 1,euler[2*N];
int tinanc[N],toutanc[N],anc = 1;
int td1 = 0,td2 = 0; /// the ends of the diameter of the whole tree
struct qry{
int l,r,u;
};
void dfs(int x,int par){
what[clk] = x;
tin[x] = clk++;
euler[ind++] = x;
tinanc[x] = anc++;
up[x][0] = par;
for(int j = 1; j <= 17; j++){
up[x][j] = up[up[x][j-1]][j-1];
}
for(auto f : g[x]){
if(f == par) continue;
dep[f] = dep[x]+1;
dfs(f,x);
euler[ind++] = x;
clk++;
}
tout[x] = clk-1;
toutanc[x] = anc;
}
bool ancestor(int u,int v){
return (tinanc[u] <= tinanc[v] && toutanc[u] >= toutanc[v]);
}
int lca(int u,int v){
if(ancestor(u,v)) return u;
if(ancestor(v,u)) return v;
int nd = u;
for(int j = 17; j >= 0; j--){
if(up[nd][j] && !ancestor(up[nd][j],v)){
nd = up[nd][j];
}
}
return up[nd][0];
}
int dist(int u,int v){
int c = lca(u,v);
return (dep[u]+dep[v]-2*dep[c]);
}
int calc(int k,int nd1,int nd2){ /// knowing the diameter of the smaller tree, we can find the needed node
int diam = dist(nd1,nd2);
if(k < (diam+1)/2) return 0;
int maxi1 = (dist(nd1,td1) > dist(nd1,td2) ? td1 : td2);
int maxi2 = (dist(nd2,td1) > dist(nd2,td2) ? td1 : td2);
int val1 = max(dist(maxi1,nd1),dist(maxi1,nd2));
int val2 = max(dist(maxi2,nd1),dist(maxi2,nd2));
int val = max(val1,val2);
if(k > val) return 0;
/// now find that vertex?
return 1;
}
void solve(int lf,int rg,vector <qry> d,int nd1,int nd2){
vector <qry> nxt;
for(int j = 0; j < d.size(); j++){
if(d[j].l <= lf && d[j].r >= rg){ /// updating the diameter of the smaller tree when adding a new special vertex
int nd = d[j].u;
if(nd1 == 0 && nd2 == 0){
nd1 = nd2 = d[j].u;
continue;
}
int d = dist(nd1,nd2),d1 = dist(nd1,nd),d2 = dist(nd,nd2);
int maxi = max({d,d1,d2});
if(maxi == d1) nd2 = nd;
else if(maxi == d2) nd1 = nd;
}
else if(d[j].l <= rg && d[j].r >= lf) nxt.push_back(d[j]);
}
if(lf == rg){
if(typ[lf] == 3) ans[lf] = calc(param[lf],nd1,nd2);
return;
}
int mid = lf+(rg-lf)/2;
solve(lf,mid,nxt,nd1,nd2);
solve(mid+1,rg,nxt,nd1,nd2);
}
void full_diam(){ /// find the diameter of the whole tree for later
queue <int> q;
q.push(1);
vector <bool> visited(n+1,0);
visited[1] = 1;
int najd = 0;
while(!q.empty()){
int u = q.front();
q.pop();
najd = u;
for(auto f : g[u]){
if(!visited[f]){
q.push(f);
visited[f] = 1;
}
}
}
for(int i = 1; i <= n; i++) visited[i] = 0;
q.push(najd);
visited[najd] = 1;
int najd1 = 0;
while(!q.empty()){
int u = q.front();
q.pop();
najd1 = u;
for(auto f : g[u]){
if(!visited[f]){
q.push(f);
visited[f] = 1;
}
}
}
td1 = najd;
td2 = najd1;
}
void cleareverything(){
for(int i = 0; i <= n+1; i++){
typ[i] = param[i] = frst[i] = spec[i] = 0;
g[i].clear();
for(int j = 0; j <= 19; j++) up[i][j] = 0;
dep[i] = tin[i] = tout[i] = 0;
tinanc[i] = toutanc[i] = 0;
}
for(int i = 0; i <= 2*n+1; i++){
for(int j = 0; j <= 19; j++) depval[i][j] = spdep[i][j] = 0;
logs[i] = what[i] = 0;
euler[i] = 0;
}
clk = ind = anc = 1;
td1 = td2 = 0;
}
void tstcase(){
cin >> n;
cleareverything();
for(int i = 1; i < n; i++){
int u,v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
full_diam();
for(int i = 1; i < 2*n; i++){
depval[i][0] = dep[euler[i]];
spdep[i][0] = euler[i];
}
for(int j = 1; j <= 18; j++){
for(int i = 1; i+(1<<j)-1 < 2*n; i++){
int val = min(depval[i][j-1],depval[i+(1<<(j-1))][j-1]);
int nd = (val == depval[i][j-1] ? spdep[i][j-1] : spdep[i+(1<<(j-1))][j-1]);
depval[i][j] = val;
spdep[i][j] = nd;
}
}
for(int i = 2; i < 2*n; i++) logs[i] = logs[i/2]+1;
cin >> q;
vector <qry> v;
for(int i = 1; i <= q; i++){
cin >> typ[i] >> param[i];
if(typ[i] == 1){
frst[param[i]] = i;
spec[param[i]] = 1;
}
else if(typ[i] == 2){
v.push_back({frst[param[i]],i,param[i]});
spec[param[i]] = 0;
}
}
for(int i = 1; i <= n; i++){
if(spec[i]) v.push_back({frst[i],q,i});
}
solve(1,q,v,0,0);
for(int i = 1; i <= q; i++){
if(typ[i] == 3) cout << ans[i];
}
cout << "\n";
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
//freopen("tst.txt","r",stdin);
int t;
cin >> t;
while(t--){
tstcase();
}
}
Tester's Solution
/* in the name of Anton */
/*
Compete against Yourself.
Author - Aryan (@aryanc403)
Atcoder library - https://atcoder.github.io/ac-library/production/document_en/
*/
#ifdef ARYANC403
#include <header.h>
#else
#pragma GCC optimize ("Ofast")
#pragma GCC target ("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx")
//#pragma GCC optimize ("-ffloat-store")
#include<bits/stdc++.h>
#define dbg(args...) 42;
#endif
// http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2016/p0200r0.html
template<class Fun> class y_combinator_result {
Fun fun_;
public:
template<class T> explicit y_combinator_result(T &&fun): fun_(std::forward<T>(fun)) {}
template<class ...Args> decltype(auto) operator()(Args &&...args) { return fun_(std::ref(*this), std::forward<Args>(args)...); }
};
template<class Fun> decltype(auto) y_combinator(Fun &&fun) { return y_combinator_result<std::decay_t<Fun>>(std::forward<Fun>(fun)); }
using namespace std;
#define fo(i,n) for(i=0;i<(n);++i)
#define repA(i,j,n) for(i=(j);i<=(n);++i)
#define repD(i,j,n) for(i=(j);i>=(n);--i)
#define all(x) begin(x), end(x)
#define sz(x) ((lli)(x).size())
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#define endl "\n"
typedef long long int lli;
typedef long double mytype;
typedef pair<lli,lli> ii;
typedef vector<ii> vii;
typedef vector<lli> vi;
const auto start_time = std::chrono::high_resolution_clock::now();
void aryanc403()
{
#ifdef ARYANC403
auto end_time = std::chrono::high_resolution_clock::now();
std::chrono::duration<double> diff = end_time-start_time;
cerr<<"Time Taken : "<<diff.count()<<"\n";
#endif
}
long long readInt(long long l, long long r, char endd) {
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true) {
char g=getchar();
if(g=='-') {
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g&&g<='9') {
x*=10;
x+=g-'0';
if(cnt==0) {
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd) {
if(is_neg) {
x=-x;
}
assert(l<=x&&x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret="";
int cnt=0;
while(true) {
char g=getchar();
assert(g!=-1);
if(g==endd) {
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt&&cnt<=r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l,r,' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l,r,'\n');
}
string readStringLn(int l, int r) {
return readString(l,r,'\n');
}
string readStringSp(int l, int r) {
return readString(l,r,' ');
}
void readEOF(){
assert(getchar()==EOF);
}
vi readVectorInt(int n,lli l,lli r){
vi a(n);
for(int i=0;i<n-1;++i)
a[i]=readIntSp(l,r);
a[n-1]=readIntLn(l,r);
return a;
}
const lli INF = 0xFFFFFFFFFFFFFFFL;
lli seed;
mt19937 rng(seed=chrono::steady_clock::now().time_since_epoch().count());
inline lli rnd(lli l=0,lli r=INF)
{return uniform_int_distribution<lli>(l,r)(rng);}
class CMP
{public:
bool operator()(ii a , ii b) //For min priority_queue .
{ return ! ( a.X < b.X || ( a.X==b.X && a.Y <= b.Y )); }};
void add( map<lli,lli> &m, lli x,lli cnt=1)
{
auto jt=m.find(x);
if(jt==m.end()) m.insert({x,cnt});
else jt->Y+=cnt;
}
void del( map<lli,lli> &m, lli x,lli cnt=1)
{
auto jt=m.find(x);
if(jt->Y<=cnt) m.erase(jt);
else jt->Y-=cnt;
}
bool cmp(const ii &a,const ii &b)
{
return a.X<b.X||(a.X==b.X&&a.Y<b.Y);
}
#include <algorithm>
#include <cassert>
#include <vector>
namespace atcoder {
struct dsu {
public:
dsu() : _n(0) {}
explicit dsu(int n) : _n(n), parent_or_size(n, -1) {}
int merge(int a, int b) {
assert(0 <= a && a < _n);
assert(0 <= b && b < _n);
int x = leader(a), y = leader(b);
if (x == y) return x;
if (-parent_or_size[x] < -parent_or_size[y]) std::swap(x, y);
parent_or_size[x] += parent_or_size[y];
parent_or_size[y] = x;
return x;
}
bool same(int a, int b) {
assert(0 <= a && a < _n);
assert(0 <= b && b < _n);
return leader(a) == leader(b);
}
int leader(int a) {
assert(0 <= a && a < _n);
if (parent_or_size[a] < 0) return a;
return parent_or_size[a] = leader(parent_or_size[a]);
}
int size(int a) {
assert(0 <= a && a < _n);
return -parent_or_size[leader(a)];
}
std::vector<std::vector<int>> groups() {
std::vector<int> leader_buf(_n), group_size(_n);
for (int i = 0; i < _n; i++) {
leader_buf[i] = leader(i);
group_size[leader_buf[i]]++;
}
std::vector<std::vector<int>> result(_n);
for (int i = 0; i < _n; i++) {
result[i].reserve(group_size[i]);
}
for (int i = 0; i < _n; i++) {
result[leader_buf[i]].push_back(i);
}
result.erase(
std::remove_if(result.begin(), result.end(),
[&](const std::vector<int>& v) { return v.empty(); }),
result.end());
return result;
}
private:
int _n;
std::vector<int> parent_or_size;
};
} // namespace atcoder
#define rep(i, a, b) for(int i = a; i < (b); ++i)
#define trav(a, x) for(auto& a : x)
// #define all(x) begin(x), end(x)
// #define sz(x) (int)(x).size()
typedef long long ll;
typedef pair<int, int> pii;
// typedef vector<int> vi;
typedef vector<pii> vpi;
typedef vector<vpi> graph;
graph readTree(lli n){
graph e(n);
atcoder::dsu d(n);
for(lli i=1;i<n;++i){
const lli u=readIntSp(1,n)-1;
const lli v=readIntLn(1,n)-1;
e[u].pb({v,1});
e[v].pb({u,1});
d.merge(u,v);
}
assert(d.size(0)==n);
return e;
}
template<class T>
struct RMQ {
vector<vector<T>> jmp;
RMQ(const vector<T>& V) {
int N = sz(V), on = 1, depth = 1;
while (on < N) on *= 2, depth++;
jmp.assign(depth, V);
rep(i,0,depth-1) rep(j,0,N)
jmp[i+1][j] = min(jmp[i][j],
jmp[i][min(N - 1, j + (1 << i))]);
}
T query(int a, int b) {
assert(a < b); // or return inf if a == b
int dep = 31 - __builtin_clz(b - a);
return min(jmp[dep][a], jmp[dep][b - (1 << dep)]);
}
};
struct LCA {
vi time;
vector<ll> dist;
RMQ<pii> rmq;
LCA(graph& C) : time(sz(C), -99), dist(sz(C)), rmq(dfs(C)) {}
vpi dfs(graph& C) {
vector<tuple<int, int, int, ll>> q(1);
vpi ret;
int T = 0, v, p, d; ll di;
while (!q.empty()) {
tie(v, p, d, di) = q.back();
q.pop_back();
if (d) ret.emplace_back(d, p);
time[v] = T++;
dist[v] = di;
trav(e, C[v]) if (e.first != p)
q.emplace_back(e.first, v, d+1, di + e.second);
}
return ret;
}
int query(int a, int b) {
if (a == b) return a;
a = time[a], b = time[b];
return rmq.query(min(a, b), max(a, b)).second;
}
ll distance(int a, int b) {
int lca = query(a, b);
return dist[a] + dist[b] - 2 * dist[lca];
}
};
vii readQueries(const lli n,const lli q){
vii queries;
vi pvrType(n,2);
lli curSpecial=0;
lli type3cnt=0;
for(lli it=0;it<q;++it){
const lli type=readIntSp(1,3);
if(type<3){
const lli vertex=readIntLn(1,n)-1;
assert(pvrType[vertex]!=type);
if(type==1)
curSpecial++;
else
curSpecial--;
pvrType[vertex]=type;
queries.pb({type,vertex});
} else {
const lli k=readIntLn(0,n-1);
assert(curSpecial>=1);
queries.pb({type,k});
type3cnt++;
}
}
assert(type3cnt>=1);
return queries;
}
void solve(lli &maxN,lli &maxQ){
const lli N5=1e5;
const lli n=readIntLn(1,min(maxN,2*N5));maxN-=n;
auto g=readTree(n);
const lli q=readIntLn(1,min(maxQ,2*N5));maxQ-=q;
const auto queries=readQueries(n,q);
vector<vi> currentVertex(4*q);
auto addSegtree=y_combinator([&](const auto &self,lli id,lli l,lli r,lli L,lli R,lli vertex)->void{
if(r<L||R<l)
return;
if(L<=l&&r<=R){
currentVertex[id].pb(vertex);
return;
}
lli m=(l+r)/2;
self(2*id,l,m,L,R,vertex);
self(2*id+1,m+1,r,L,R,vertex);
});
auto add=[&](lli L,lli R,lli vertex){
addSegtree(1,0,q-1,L,R,vertex);
};
lli curIdx=0;
vi type1Last(n,-1),queryDistance;
for(auto [type,vertex]:queries){
if(type==3){
curIdx++;
queryDistance.pb(vertex);
continue;
}
if(type==1){
type1Last[vertex]=curIdx;
continue;
}
if(type==2){
const lli L=type1Last[vertex],R=curIdx-1;
type1Last[vertex]=-1;
add(L,R,vertex);
continue;
}
}
for(lli vertex=0;vertex<n;++vertex){
if(type1Last[vertex]==-1)
continue;
const lli L=type1Last[vertex],R=curIdx-1;
type1Last[vertex]=-1;
add(L,R,vertex);
}
if(n==1){
cout<<string(curIdx,'1')<<endl;
return;
}
LCA lca(g);
vector<bool> ans(curIdx);
auto findDiameter=[&](lli d1,lli d2,lli cur)->ii{
if(d1==-1){
d1=cur;
} else if(d2==-1){
d2=cur;
} else {
const lli cd=lca.distance(d1,d2);
const lli cd1=lca.distance(d1,cur);
const lli cd2=lca.distance(d2,cur);
if(cd>=cd1&&cd>=cd2)
return {d1,d2};
if(cd1>=cd2)
return {d1,cur};
return {d2,cur};
}
return {d1,d2};
};
lli D1=-1,D2=-1;
for(lli i=0;i<n;++i)
tie(D1,D2)=findDiameter(D1,D2,i);
auto findVertex=[&](lli d1,lli d2,lli dist)->bool{
if(d2!=-1&&lca.distance(d1,d2)>2*dist)
return false;
if(lca.distance(D1,D2)<dist)
return false;
if(lca.distance(D1,d1)>=dist||lca.distance(D2,d1)>=dist)
return true;
if(d2==-1)
return false;
if(lca.distance(D1,d2)>=dist||lca.distance(D2,d2)>=dist)
return true;
return false;
};
y_combinator([&](const auto &build,lli id,lli l,lli r,lli d1,lli d2)->void{
for(auto &vertex:currentVertex[id]){
tie(d1,d2)=findDiameter(d1,d2,vertex);
}
if(l>=sz(ans))
return;
if(l==r){
ans[l]=findVertex(d1,d2,queryDistance[l]);
dbg(l,d1,d2,D1,D2,ans[l]);
return;
}
lli m=(l+r)/2;
build(2*id,l,m,d1,d2);
build(2*id+1,m+1,r,d1,d2);
})(1,0,q-1,-1,-1);
for(auto x:ans)
cout<<x;
cout<<endl;
}
int main(void) {
ios_base::sync_with_stdio(false);cin.tie(NULL);
// freopen("txt.in", "r", stdin);
// freopen("txt.out", "w", stdout);
// cout<<std::fixed<<std::setprecision(35);
lli T=readIntLn(1,200);
lli maxN=4e5,maxQ=4e5;
while(T--)
{
solve(maxN,maxQ);
} aryanc403();
readEOF();
return 0;
}
Editorialist's Implementation
#include <bits/stdc++.h>
#define LL long long
#define rst(x) memset(x, 0, sizeof(x))
using namespace std;
clock_t start = clock();
const int N = (int)2e5 + 5;
vector<int> g[N];
// mxDep[i] = node with maximum depth in the subtree of node i (tree is rooted at 1)
// depth[i] = depth of the tree when rooted at 1
// eulerTour := array describing the euler tour of the tree
// inTime[i] := first occurrence of node i in the euler tour
int mxDep[N], depth[N], eulerTour[N + N], inTime[N];
// Du, Dv = endpoints of the diameter of the tree
// mx1, mx2 = variables used in the dfs to compute Du, Dv
int Du, Dv, D, dfsTime, mx1, mx2;
void dfs(int u, int p) {
// set depth, inTime and eulerTour
depth[u] = depth[p] + 1;
inTime[u] = dfsTime;
eulerTour[dfsTime++] = u;
// regular dfs
for (auto &v : g[u]) if (v != p) {
dfs(v, u);
eulerTour[dfsTime++] = u;
}
// Computing diameter of the tree
mx1 = u; mx2 = u;
for (auto &v : g[u]) if (v != p) {
int upd = mxDep[v];
if (depth[upd] >= depth[mx1]) {
mx2 = mx1;
mx1 = upd;
} else if (depth[upd] >= depth[mx2]) {
mx2 = upd;
}
}
mxDep[u] = mx1;
if (D < depth[mx1] + depth[mx2] - 2 * depth[u]) {
D = depth[mx1] + depth[mx2] - 2 * depth[u];
Du = mx1;
Dv = mx2;
}
}
// Sparse table over the eulerTour for fast distance queries
const int lgN = 20;
int sparseTable[lgN][N + N];
void setupSparseTable() {
for (int i=0;i<dfsTime;++i) {
sparseTable[0][i] = eulerTour[i];
}
for (int j=1;j<lgN;++j) {
for (int i=0;i+(1<<j)<=dfsTime;++i) {
int u = sparseTable[j-1][i], v = sparseTable[j-1][i+(1<<(j-1))];
sparseTable[j][i] = (depth[u] < depth[v] ? u : v);
}
}
}
// computing the LCA of nodes u, v
int lca(int u, int v) {
int l = inTime[u], r = inTime[v];
if (l > r) swap(l, r);
int j = __builtin_clz(1) - __builtin_clz(r - l + 1);
int L = sparseTable[j][l], R = sparseTable[j][r-(1<<j)+1];
return (depth[L] < depth[R] ? L : R);
}
// computing the distance between nodes u, v
int dist(int u, int v) {
if (u == 0 || v == 0) return -1;
return depth[u] + depth[v] - 2 * depth[lca(u, v)];
}
// Segment tree variable :
// treeD[i] = Diameter of special nodes represented by node i
// treeU[i], treeV[i] = End points of the diameter of special nodes represented by node i
int treeD[N * 4], treeU[N * 4], treeV[N * 4];
void merge(int node, int lef, int rig) {
treeD[node] = -1;treeU[node] = 0; treeV[node] = 0;
for (auto u : {treeU[lef], treeU[rig], treeV[lef], treeV[rig]}) {
for (auto v : {treeU[lef], treeU[rig], treeV[lef], treeV[rig]}) {
int d = dist(u, v);
if (d > treeD[node]) {
treeD[node] = d;
treeU[node] = u;
treeV[node] = v;
}
}
}
}
// Lazy range updates
void update(int pos, int type, int node, int st, int en) {
if (st == en) {
if (type == 1) {
treeD[node] = 0; treeU[node] = treeV[node] = pos;
} else {
treeD[node] = -1; treeU[node] = 0; treeV[node] = 0;
}
return;
}
int m = (st + en) >> 1;
if (pos <= m) update(pos, type, 2*node + 1, st, m);
else update(pos, type, 2*node+2, m+1, en);
merge(node, node*2+1, node*2+2);
}
void solve() {
int n;
cin >> n;
for (int i=1;i<=n;++i) {
g[i].clear();
}
for (int i=1;i<n;++i) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
Du = Dv = 0; dfsTime = 0;D = -1;
dfs(1, 0);
setupSparseTable();
for (int i=0;i<=4*n;++i) {
treeD[i] = -1;
treeU[i] = treeV[i] = 0;
}
int q;
cin >> q;
while(q--) {
int type;
cin >> type;
if (type == 3) {
int d = treeD[0], u = treeU[0], v = treeV[0], K;
cin >> K;
if (2 * K < d) {
cout << 0;
continue;
} else {
int mx = max({dist(u, Du), dist(u, Dv), dist(v, Du), dist(v, Dv)});
cout << (mx >= K);
}
} else {
int u;
cin >> u;
update(u, type, 0, 1, n);
}
}
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(false);cin.tie(NULL);
int T;
cin >> T;
for (int t=1;t<=T;++t) {
solve();
}
return 0;
}