Problem Link:
Clash Wildcard 2022
Practice
Approach:
Denote w(v) the number of leaves in the subtree of v. Suppose that a non-leaf vertex v has children u_1, ... u_k, and the numbers to arrange in the leaves are 1, …, w(v). We are not yet sure how to arrange the numbers but we assume for now that we know everything we need about the children’s subtrees.
Okay, what is the maximal number we can achieve if the maximizing dog moves first? Clearly, it will choose the subtree optimally for itself, and we are eager to help it. Thus, it makes sense to put all the maximal numbers in a single subtree; indeed, if any of the maximal numbers is not in the subtree where the first dog will go, we swap it with some of the not-so-maximal numbers and make the situation even better. If we place w(u_i) maximal numbers (that is, w(v) - w(u_i) + 1, ... w(v)) in the subtree of w(u_i), we must also arrange them optimally; this task is basically the same as arranging the numbers from 1 to w(u_i) in the subtree of w(u_i), but now the minimizing dog goes first. Introduce the notation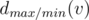 
for the maximal possible result if the maximizing/minimizing (depending on the lower index) dog starts. From the previous discussion we obtain 
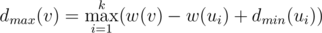. Thus, if we know 
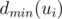for all children, the value of 
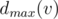can be determined.
How does the situation change when the minimizing dog goes first? Suppose that for each ‘i’ we assign numbers 1, ..., n_1, w(u_i) to the leaves of the subtree of u_i in some order; the numbers in the subtree of u_i will be arranged so that the result is maximal when the maximizing dog starts in u_i. Suppose that numbers n_ {i, j} are sorted by increasing of j for every i; the minimizing dog will then choose the subtree u_i in such a way that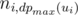 
is minimal. For every arrangement, the minimizing dog can guarantee itself the result of at most 
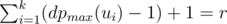. Indeed, if all the numbers 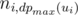are greater than r, all the numbers n_ {i, j} for 
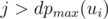should also be greater than r; but there are 
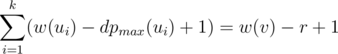numbers n_ {i, j} that should be greater than r, while there are only w(v) - r possible numbers from 1 to w(v) to place; a contradiction (pigeonhole principle). On the other hand, the value of r is easily reachable: place all the numbers less than r as n_ {i, j} with 
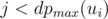, and r as, say, n_1, dp max(u_1); the first player will have to move to u_1 to achieve r. Thus, 
.
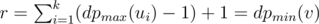The previous, rather formal argument can be intuitively restated as follows: suppose we put the numbers from 1 to w(v) in that order to different subtrees of v. Once a subtree of u_i contains dp max(u_i) numbers, the minimizing dog can go to u_i and grab the current result. It follows that we may safely put dp max(u_i) - 1 numbers to the subtree of u(i) for each i, and the next number (exactly r) will be grabbed regardless of what we do (if we do not fail and let the minimizing dog grab a smaller number).
Setter's Solution (C++)
#include <iostream>
#include <vector>
#include <cmath>
#include <ctime>
#include <cassert>
#include <cstdio>
#include <queue>
#include <set>
#include <map>
#include <fstream>
#include <cstdlib>
#include <string>
#include <cstring>
#include <algorithm>
#include <numeric>
#define mp make_pair
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef long long i64;
typedef vector<i64> vi64;
typedef vector<vi64> vvi64;
template<class T>
bool uin(T &a, T b) {
if (a > b) {
a = b;
return true;
}
return false;
}
template<class T>
bool uax(T &a, T b) {
if (a < b) {
a = b;
return true;
}
return false;
}
const int MAXN = 210000;
vi e[MAXN];
int w[MAXN];
int dpmax[MAXN], dpmin[MAXN];
void dfs(int v) {
if (e[v].empty()) {
w[v] = 1;
dpmax[v] = dpmin[v] = 0;
return;
}
int md = 1e9, s = 0;
w[v] = 0;
for (int u: e[v]) {
dfs(u);
w[v] += w[u];
uin(md, dpmin[u]);
s += w[u] - dpmax[u];
}
dpmax[v] = w[v] - md - 1;
dpmin[v] = s - 1;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.precision(10);
cout << fixed;
#ifdef LOCAL_DEFINE
freopen("input.txt", "rt", stdin);
#endif
int N;
cin >> N;
forn(i, N - 1) {
int x, y;
cin >> x >> y;
e[--x].pb(--y);
}
dfs(0);
cerr << w[0] << '\n';
cout << dpmax[0] + 1 << ' ' << dpmin[0] + 1 << '\n';
#ifdef LOCAL_DEFINE
cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
return 0;
}