PROBLEM LINK:
Author: Bruno Oliveira
Tester: Mahbubul Hasan
Editorialist: Jingbo Shang
DIFFICULTY:
Medium
PREREQUISITES:
Suffix Array, Suffix Automaton, Binary Search, Hash
PROBLEM:
Find the longest common substring (LCS, consecutive) of two given strings S, T.
We have added test cases before the contest ended. Therefore, we extend the contest for one day.
EXPLANATION:
This problem is a classical problem. The setter is inspired by SPOJ LCS. However, in this problem, the only approach which gets AC is Suffix Automaton, so, by allowing different approaches like Hashing and Suffix Arrays to pass in the Codechef problem. And the main purpose of author is to teach new data structures to many new people
There are several solutions such as Suffix Array, Suffix Automaton, Binary Search + Hash. Here, I would like to introduce two of them, Suffix Automaton and Binary Search + Hash.
Binary Search + Hash
It is clear that the length of the LCS can be binary search. That is, if we have a common substring with length L, we can always find common substring with length less than L. Therefore, the binary search framework is as following:
lower = 0, upper = maxlength + 1; // LCS in [lower, upper).
while (lower + 1 < upper) {
middle = (lower + upper) / 2;
if (there is some common substring with length middle) {
lower = middle;
} else {
upper = middle;
}
}
LCS = lower;
So, the key point here is to check whether there is some common substrings with length middle. A usual way is to adopt Hash. For my preference, I would like to use Rabin-Karp hash, which is treat a string like a MAGIC based number. That is,
Hash(S[0..n-1]) = (S[n-1] * MAGIC^0 + S[n-2] * MAGIC^1 + .. + S[n-1-i] * MAGIC^i + ... ) % MOD
The most convenient point here, is that we can use Hash(S[0…i]) to calculate the Hash(S[l…r]) in O(1) time, with O(N) preparation. That is,
Hash(S[l..r]) = (Hash(S[0..r]) - Hash(S[0..l-1]) * MAGIC^(r-l+1)) % MOD
Therefore, we can get all hash values of substring with length middle from two given strings, and then, check whether there is any overlap. This procedure can be done via Hash Table in O(|S|) or Set (Balanced Binary Search Tree) in O(|S|log|S|). Therefore, Binary Search + Hash can solve this problem in O(|S| log|S|) time.
Suffix Automaton (Thanks to Bruno, the setter)
An automaton M is a 5-tuple which is composed in a very broad and general way by:
- A set of states, Q;
- A special state, defined as q0, also known as the start state;
- A set of accept states, A, which is a subset of Q.
- A given input alphabet.
- A special function which will allow for transitions between states, known as transition function.
While the theory on finite automaton is very vast and somewhat complex, from the point of view of our problem, we just need to know how to “map” all of the above concepts to what can be called a String-matching Automaton, which is just like a regular automaton with some added information in between the states and with additional characteristics which rely on the texts we intend to match, and also, of course, on the alphabet which is being to used to compose the texts themselves.
Below is a simple drawing of an automation, which accepts strings which end in the pattern “GCAGAGAG” (contains it as a suffix). 8 is the accept state. 0 is the start state. The arrows show the transition function.
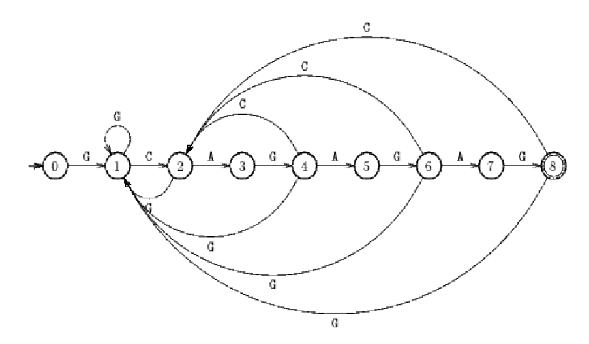
The main idea here is that the automaton will only reach its accepting state (the one on the node 8, circled twice), when the entire pattern is found on the string.
Then, the high level idea, to actually make a matcher based upon an automaton possible is that we will use an “online” algorithm in the sense that we process each character individually by applying the transition function mentioned earlier. When we reach an accepting state, we can simply output the shift with which the accepting state occurred in the original string, and we will have the exact location of the matching.
An automaton in practice
After this very brief introduction about automatons, we are now ready to see some code, which is actually quite simple if the above explanation is taken into account. The main support structure for our automaton is what a state is, which can be defined in C++ as:
struct state {
int len, link ;
map < char , int > next; // if the alphabet is small, we can also use the array of constant size.
} ;
where we have the total length of the automaton so far, the link which is responsible to simulate the “connection” between nodes and a map<char, int> next which is responsible for denoting the “next” state in the automaton, composed obviously of a character and a link. Taken into account that the construction of the automaton is done “online”, by adding characters one by one, we can actually do it by extending the existing automaton with a specific character. That is done in the function called, sa_extend, presented below and which stands for suffix automaton extend:
void sa_extend ( char c ) {
int cur = sz ++ ;
st [ cur ] . len = st [ last ] . len + 1 ;
int p ;
for ( p = last ; p ! = - 1 && ! st [ p ] . next . count ( c ) ; p = st [ p ] . link )
st [ p ] . next [ c ] = cur ;
if ( p == - 1 )
st [ cur ] . link = 0 ;
else {
int q = st [ p ] . next [ c ] ;
if ( st [ p ] . len + 1 == st [ q ] . len )
st [ cur ] . link = q ;
else {
int clone = sz ++ ;
st [ clone ] . len = st [ p ] . len + 1 ;
st [ clone ] . next = st [ q ] . next ;
st [ clone ] . link = st [ q ] . link ;
for ( ; p ! = - 1 && st [ p ] . next [ c ] == q ; p = st [ p ] . link )
st [ p ] . next [ c ] = clone ;
st [ q ] . link = st [ cur ] . link = clone ;
}
}
last = cur ;
}
Now, all there is left to be done is to show how to initialize the automaton, done in the function sa_init by adding a “fake” state which links to nowhere, since the automaton initially only has its start state q0:
void sa_init ( ) {
sz = last = 0 ;
st [ 0 ] . len = 0 ;
st [ 0 ] . link = - 1 ;
++ sz ;
` }
To find the LCS of two strings with an automaton, we can augment our variables such that we maintain a current length and a current state and simply choose to perform a transition between states if no match is found, or, we might choose to augment and update a link in order to “tell” to the automaton that we can keep on extending our links because we are in the middle of the matching.
In pseudo-code:
lcs( s, t ) {
sa_init ( ) ;
for ( i=0 ; i < length(s) ; ++ i )
sa_extend ( s [ i ] ) ;
int v = 0 , l = 0 ,
best = 0 , bestpos = 0 ;
for ( i=0 ; i < length (t) ; ++ i ) {
while ( v && ! st [ v ] . next . count ( t [ i ] ) ) {
v = st [ v ] . link ;
l = st [ v ] . length ;
}
if ( st [ v ] . next . count ( t [ i ] ) ) {
v = st [ v ] . next [ t [ i ] ] ;
++ l ;
}
if ( l > best )
best = l, bestpos = i ;
}
return best_substring ;
}
In summary, we can solve this problem using Suffix Automaton in O(|S|) time.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
 Especially people who are definitely more skilled than I am!!
Especially people who are definitely more skilled than I am!!