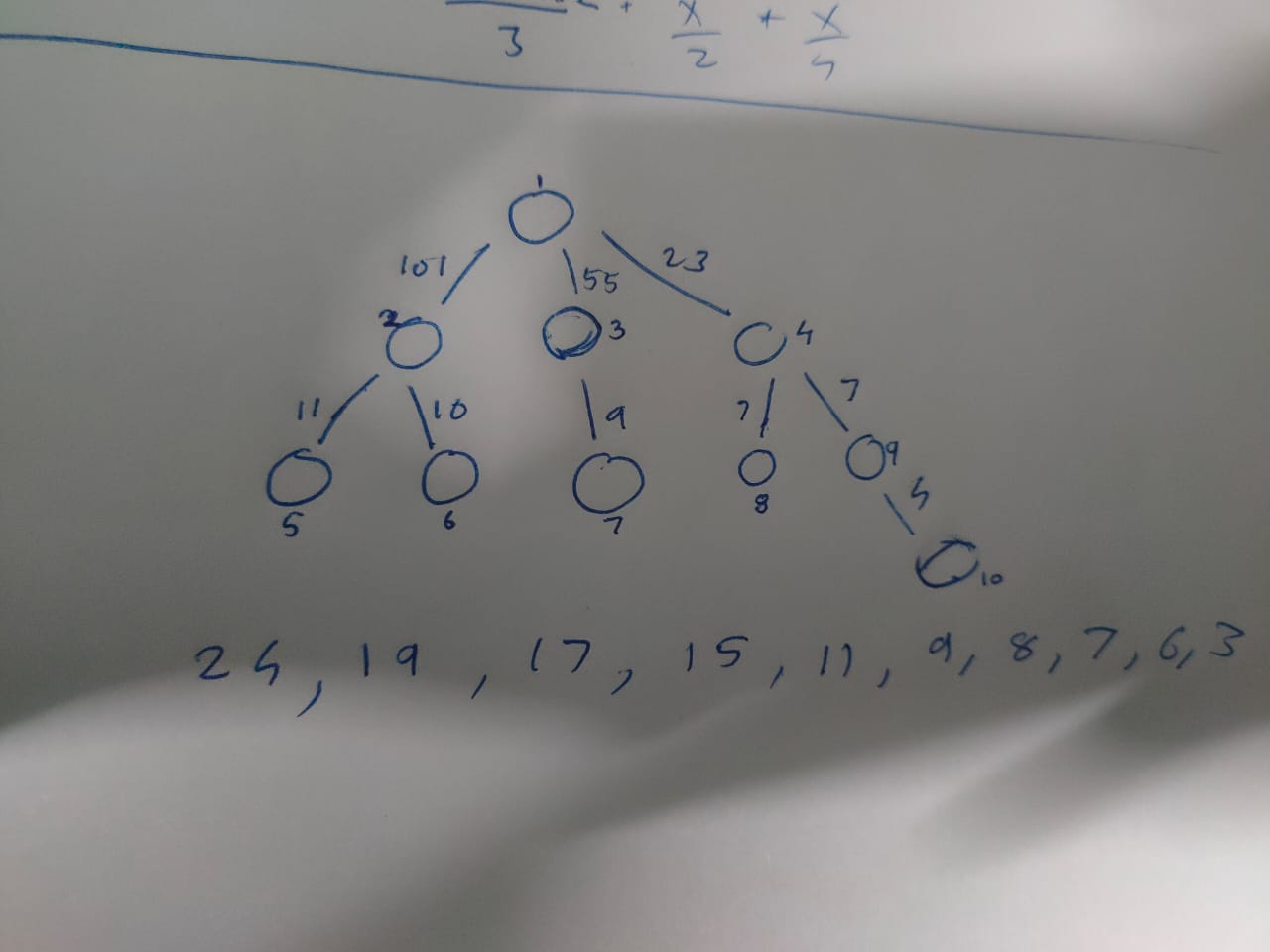Can someone show how to solve Sticky Notes from December Long Challenge
Link to problem : CodeChef: Practical coding for everyone
The solution is independent of the graph
Sort the edge weights and the node values in descending order.
The heaviest edge has to be assigned to 2 nodes (i.e. 2 nodes should have value greater than the heaviest edge) and after that the remaining edges can be assigned to 1 node. See how many node values you have to upgrade and that will be the answer
This is very easy problem, easier than three other most solved problems in div 1.
As problem statement says u can swap edges and vertices. That means you can change tree in whatever form. That means tree structure doesn’t even matter here.
As required you need to put edge Ei between two nodes Vx and Vy such that Value(Vx) >= Value(Ei) <= Value(Vy)
Thus insert N-1 values in N values such that above condition meets.
The idea is to sort both N-1 edge values and N vertices values. Now try inserting first N-1 values starting from max side. If two vlaues in vertices array exists then insert else add a new value because there is no other way to insert this edge value. This way keep inserting all the edges.
For example E: 3 9 and V: 1 4 9, so u can’t insert 9 in 4 and 9 so add a value higher or equal to 9. So 9 is done. Since each vertex can further be used to connect with other vertex using new edge, we can use 4 and 9 to insert 3.
This way you added only one new value. Same approach can be extended to insert any such input.
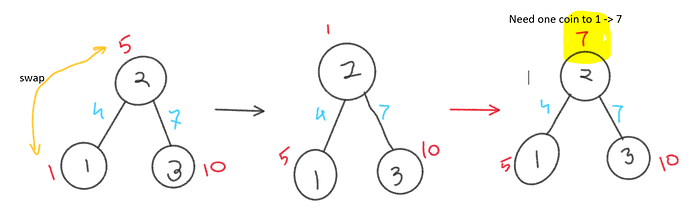
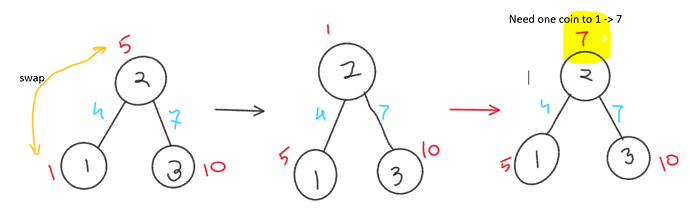
I didn’t understand how swapping edges allows us to have any tree structure that we desire. If we can only swap the edges, then only the values of the edges can change, not the tree structure right?
For example, I have drawn 2 trees below and don’t understand how one can be swapped for the other.
Here’s my solution: STICNOT the first observation is that the connections in the tree are irrelevant: as long as the multisets of edge weights and node weights are same, the solution remains the same (and you can permute them in any way you like to form any tree in your mind but as you can swap edge weights among edges and node weights among nodes, the solution is independent of the structure of the tree).
What I did was sort the edge weights and node weights in non - decreasing order. Then I traversed through the edges and for each, I searched for the first matching node (the one that obeys the given constraints) using binary search. If we don’t find a match, we pay one coin and change the weight of a vertex (so that it now equals the next edge weight in sequence and the condition is just satisfied). If we find a match, however, we delete the node so that we don’t match it with any other edge in the future. Continuing this way, we have formed exactly n - 1 matchings in the end, with the invariant that one vertex is being matched and deleted in every iteration. The remaining vertex is tested with the last edge weight and if it already follows the condition, no more coin is paid and if it doesn’t, one more coin is paid and we change its value to that of the last edge. Now join each matching together to form a tree (it is always possible as we have paid to achieve the same) and viola, you’re done ![]()
Swapping edges here means you can use them for any two vertices. Similarly swapping vertices means you can use any vertex against any edge. That means structure of tree does not matter here to solve this.
Is this a norm when it comes to competitive programming because I feel that it isn’t very self explanatory. I feel like this should’ve been mentioned more explicitly in the question. Thanks for the help though @manoharsingh23. I’ll try to think of the solution once before coming back here 
Sort the edges and the nodes in non-decreasing order.
Pick the Nodes at which are greater than the Edges from start.
Output : Total Nodes - Picked Nodes.
Solution - CodeChef: Practical coding for everyone ![]()
It felt funny after I realised this property. I did solve without knowing this, only assuming that values of edges and vertices can be swapped but the tree structure remains constant. Thanks.
can you help me out for the given example case. like why only one coin is needed ?
thanks in advance…
1
3
1 2 4
2 3 7
1 5 10
Here’s my solution and its very simple.
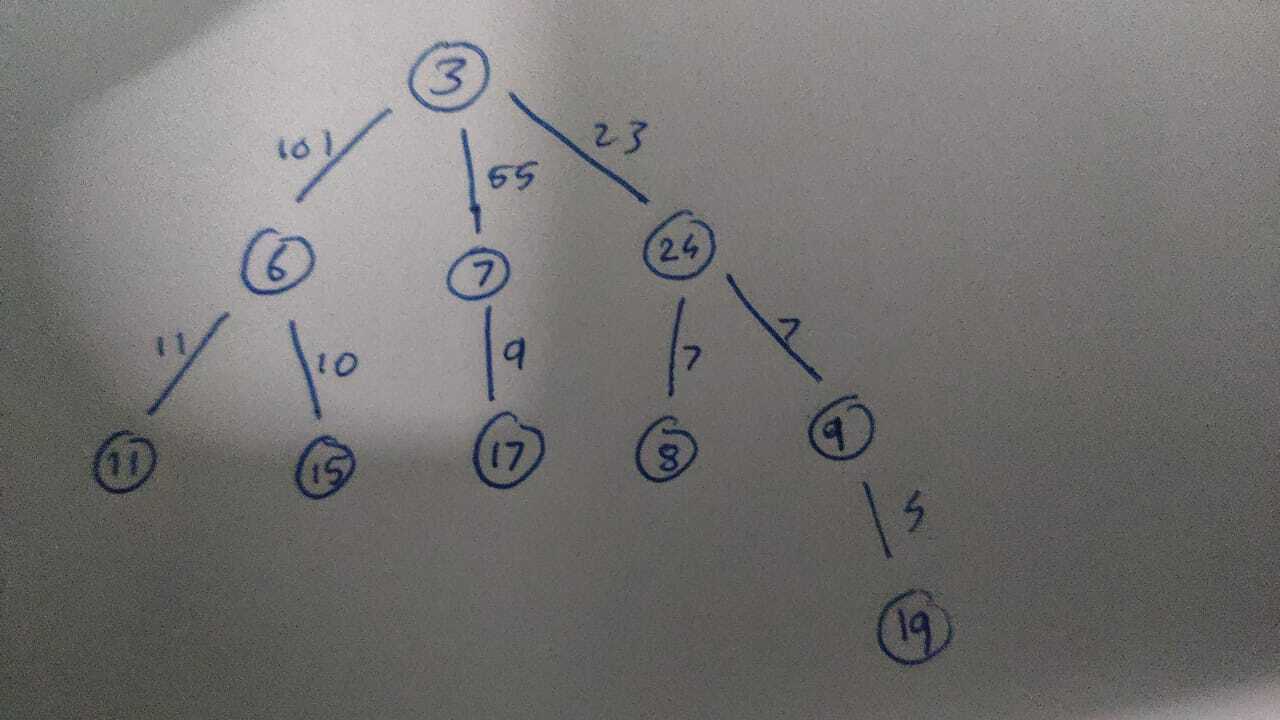
First of all arrange the edge weights in descending order of level order traversal like in the pic, and also store vertice weights in descending order in an array
Then to the vertices:
- If maxedge>maxvertice ,add minvertice ( as its gonna get swapped anyway), delete minvertice for vertice array and do count++
2.Else add “Lowerbound of maxedge in vertice array” to tree and delete it from vertice array
Do the same thing for all vertices. The value of count you get in the end will be the answer. Also this is the tree you get if you follow the above implementation with coins=3.
And here’s my solution : CodeChef: Practical coding for everyone
Made some modification to get 100: CodeChef: Practical coding for everyone
Problem Clarification
Given values of N vertex and N-1 edges. You can perform 3 operations.
- Swap vertex value
- Swap edges value
- Change vertex value - cost 1 coin per action.
You need to make all adjacent vertex values greater than or equal to the edge value i.e. av \ge be
Find out the minimum number of coins you need to satisfy the required condition.
Solution Explanation
Every edge value need two greater or equal vertex value.
To check it, we can use priority_queue.
- Take input and store edge and vertex value in a priority_queue, say
priority_queue<int> a, b;[a for vertex value, b for edge value].
Code example:
int n;
cin >> n;
priority_queue<int> a, b;
for (int i = 1, x, y, d; i < n; i++) {
cin >> x >> y >> d;
b.push(d);
}
for (int i = 0, d; i < n; i++) {
cin >> d;
a.push(d);
}
-
Count how many coins you need to achieve this, say
cnt = 0
Priority_queue keep the maximum value at the top position in c++ (java keep the minimum value at the top position). -
Now checkout the maximum value of edge, if it is greater then the vertex value, then we need 2 coins to get maximum value. i, e,
cnt += 2otherwise pop out the maximum vertex value. Now every edge need one maximum or equal vertex value to satisfy the condition.
Code Example:
int cnt = 0;
if (b.top() > a.top()) {
cnt += 2;
b.pop();
} else {
a.pop();
}
- Now loop throw all edges and check out the condition: av \ge be if condition is false, need one coin to fix it. We always use coin to change minimum vertex value, that’s why we don’t pop out vertex value. Pop out vertex value from a if the condition is true. Here is the code example:
while (!b.empty()) {
if (b.top() > a.top())
cnt++;
else
a.pop();
b.pop();
}
- Now print out the minimum coins (cnt) you need to satisfy the required condition.
cout << cnt << "\n";
That’s all 
Solution Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define sz(a) a.size()
#define all(a) a.begin(), a.end()
#define w(a) std::cerr << #a << " : " << (a) << "\n";
void solve() {
int n;
cin >> n;
priority_queue<int> a, b;
for (register int i = 1, x, y, d; i < n; i++) {
cin >> x >> y >> d;
b.push(d);
}
for (register int i = 0, d; i < n; i++) {
cin >> d;
a.push(d);
}
int cnt = 0;
if (b.top() > a.top()) {
cnt += 2;
b.pop();
} else {
a.pop();
}
while (!b.empty()) {
if (b.top() > a.top())
cnt++;
else
a.pop();
b.pop();
}
cout << cnt << "\n";
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
register int tc;
cin >> tc;
while (tc--) solve();
return 0;
}
Happy Coding 
Was able to solve it very easily given the fact that the tree can be whatever structure we want. It’s kinda unfortunate that the problem wasn’t very clear.
@adarsh_007 At first, swap vertex value 1 and 5 Then spend one coin to change vertex value 1 to 7 (or greater). Now,edge value 7 is less then or equal to 7 and 10. another edge value 4 is less then 5 and 7. So it’s satisfy required condition, hence answer is one.
@adarsh_007 So for your test case edge with values 4 and 7 needs to be inserted among 1 5 and 10.
You start from higher end for both edges and vertices. So, here we start with 7, to be tried to insert between 5 & 10. 10 is okay but 5 is lesser than 7. Since there won’t be any vertex with higher value than 5 (because they are sorted), we must have to add a new value. For doing it optimally, we should assign it to smallest vertex, because that is useless now. Suppose newly added value is 8. So, new values of vertices in increasing order are 5, 8, 10. Now, we try to insert 7 again, because it was unsuccessful earlier. 8 & 10 is working now for 7 as both the vertices having higher values than 7. Now, try inserting 4. Because 8-10 is already used, try either 5-8 or 5-10, both should be working for 4 as well. Therefore, only added new value is 8 thus number of coins to spend to add any new value is 1.
thank you very much @smile_forever @manoharsingh23 … I misunderstood the problem and the example. Even not read the Inputs carefully. LEARNING FOR ME : I will read the problem statement carefully from next time onwards. 
Simple 5 lines of code:
@adarsh_007 Don’t worry mate, rating is nothing BUT learning is everything. And this time you learn by mistake. That’s sound awesome to me.
PS. I’ve made many silly problems too…
degree can matter as one vertex value has then to satisfy 3 different edges for 3 degree vertex but a two degree vertex just has to satisfy 2 edges
Actually, structure of the tree will remain the same because we are changing the values of edges and vertices and without changing the structure of the tree(means vertex X will remains at its same pos. as it was prev. … If this remains the same then degree will also be the same). That’s why he mentioned this “That means structure of tree does not matter here to solve this”. Also, for more clarity see the following image.
Thanks to @smile_forever for this graphical image.