PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Daanish Mahajan and Srikkanth R
Tester: Istvan Nagy
Editorialist: Taranpreet Singh
DIFFICULTY
Easy
PREREQUISITES
Euler Tour, Segment Tree, Greedy
PROBLEM
Given a tree with N nodes and an integer K.A subtree is defined as a connected subgraph of the tree. That is, a subtree is another tree that can be obtained by removing some (possibly none) vertices and all edges incident to those vertices from T.
A subset S of vertices is called good if every subtree containing all the nodes in S has at least k nodes.
Find the size of the smallest good subset.
QUICK EXPLANATION
- For K = 1, we have to select only 1 node.
- If the diameter of the tree has X nodes, then we can select its endpoints as the required subset for all K \leq X
- Otherwise, after selecting endpoints of diameter in the subset, we select leafs furthest from any selected vertex greedily, till the number of nodes in induced subtree cover is at least K.
EXPLANATION
Intuition and Idea
Let’s handle the edge case with K = 1 beforehand, as we can select any 1 node.
Now, let’s see what is the largest number of nodes we can cover using a good subset of two nodes. The number of nodes in the subtree is nothing, but the number of nodes on a simple path between two nodes. By the definition, the diameter of the tree is the longest simple path present in the graph. So if the diameter of the tree is X nodes, then the subset containing endpoints of diameter is good for all K \leq X
Now, let’s say K > X, so we need to select at least 3 nodes.
Claim: We only select leaf nodes in a good subset
Proof: Let’s assume there’s a non-leaf node u inside the chosen subset. Two cases arise
- Node u has a direct neighbour not present in the subtree.
In this case, we can select that neighbour, increasing the size of the subtree covered by at least 1. hence, the choice of node u is not optimal in this case - Node u has no direct neighbour not covered in the subtree
In this case, Since node u has at least 2 neighbours, both of which are already covered, then node u is covered in subtree irrespective of including u in the subset. So we can remove node u from the subset, reducing subset size by 1 while keeping subtree size the same.
Claim: Let’s say an endpoint of diameter (a, b) is selected as the root, It is optimal to choose the root node and leaves greedily, based on the number of nodes, which shall be included in subtree by choosing this leaf.
Intuition:
I’d share my intuition on why this claim works, as complete proof is a bit tricky
- Firstly, choosing one leaf over other do not, in any way restrict us from choosing some other leaf subsequently.
- Let’s say we choose leaves a, b, c, d in this order by greedy, where a and b are diameter. See the tree image below for reference. After this, the gain by adding node c and node d shall be G_c + G_d - G_{lca(c, d}. If we change the order to a, b, d, c, the substree spanned after adding 4 nodes is same, but subtree spanned after three nodes is D+G_d instead of D+G_c where D is length of diameter. Since greedy choose c before d, then G_c \geq G_d, so if some leaf shall be added to subset, it is optimal to add them in the decreasing order of G_u.
Lastly, Let’s compare two orders a, b, u, w and a, b, v, w, where (a, b) is diameter, and first order is made by greedy approach, and second optimal. After processing diameter, we have G_u \geq G_w \geq G_v, and we have G_w - G_{lca(u, w} \geq G_v-G_{lca(u,v)} \implies G_w \geq G_v.
Note that the values G_x used are the values just after processing diameter.
The number of nodes added in first case is S_1 = D+G_u+G_w-G_{lca(u, w)} and in second case, it is S+2 = D+G_v+G_w-G_{lca(v, w)}. We aim to prove that S_1 \geq S_2 or S_1-S_2 \geq 0.
S_1-S_2 = D+G_u+G_w-G_{lca(u, w)} - (D+G_v+G_w-G_{lca(v, w)}) \implies S_1-S_2 = G_u-G_{lca(w, u)} - G_v + G_{lca(v, w)}
We already have G_u \geq G_w, and We have $$G_{lca(u, w)} \geq G_{lca(u, v)}$ implying node w is in subtree of node lca(u, v) which implies G_{v, w} \geq G_{u, v}.
Now, by considering nodes in order a, b, w, and then choosing greedily, we can see that since only one node can be choosen, we must choose the node with largest G_u-G_{u, w}, which is leads to same gain as picking nodes in order a, b, u, w. So this completes a rough intuition on why greedy works. The complete proof can be read in paper below.
Proof: The rigorous proof for this can be seen in this paper, with special emphasize on section 2.4 on Tree networks.
Implementation
After finding diameter, let’s root the tree at one end of diameter. The benefit of this is that since root of this tree is included in subset, then if we choose to include node u in subset, all ancestors of node u shall be included in subtree automatically, saving tedius implementation.
Let S denote the good subset selected till now, inc_u holds a boolean value, determining whether node u is inside subtree or not, and G_u denotes the number of new nodes, that shall be added to subtree if node u is selected.
We need a way to maintain G_u for all nodes while moving some nodes from not included to included status.
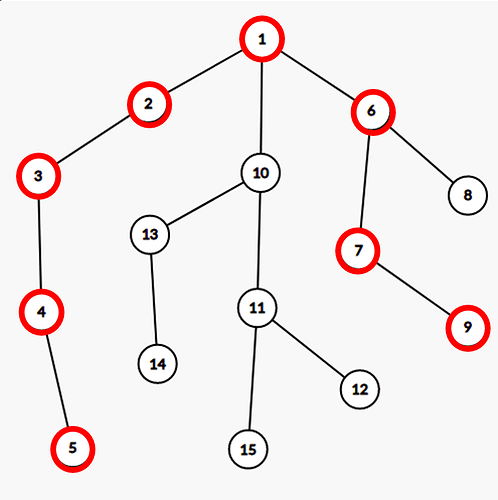
Let’s see the example below.
The path highlighted is the diameter of tree, and is already included in induced subtree by nodes 5 and node 9.
Let’s compute G_u for all non-included nodes. We have G_{10} = G_8 = 1, G_{11} = G_{13} = 2 and G_{12} = G_{14} = G_{15} = 3
Let’s say node 12 is added to subset. Now, we need to update G for all nodes not in induced subtree.
Nodes 10, 11 and 12 shall get added to induced subtree. So the resulting values would be G_8 = G_{15} = G_{13} = 1 and G_{14} = 2 We assume G_u = 0 if u is included in subtree.
Claim: If node u is added to subset, then G_v shall be reduced by G_{lca(u, v)} for all nodes v.
Proof: All nodes on path from lca(u, v) to nearest included nodes are the ones which get excluded from G_v by reducing G_v.
Hence, let’s consider nodes 10, 11 and 12 in this order as candidates for lca(12, v).
- For node 10, Both nodes 13 and node 14 has lca with 12 at node 10. So we reduce G_{13} and G_{14} by G_{10} = 1 each.
- For node 11, Only node 15 has lca with node 12 at node 11. Hence, G_{15} is reduced by G_{11}
- There’s no node with lca(v, 12) = 12
Hence, while considering node x, we iterate over all children of x not included in subtree, and reduce them by G_x.
If we build an euler tour on tree, then these transform to range decrement queries. Finding u with maximum value of G_u is just the argmax query, the position of maximum value. For removing some value, we can decrement them with N, so that they are never considered again.
Lastly, since each node shall be move from non-included to included only once, we can process nodes (like we processed 10, 11 and 12) one by one.
TIME COMPLEXITY
Diameter can be computed in O(N). Segment Tree operations take O(log(N)) per query after O(N) construction. Each node is processed only once, so the number of processed nodes is O(N) and the number of segment tree operations is proportional to the number of edges, which is O(N) as well.
Hence, the time complexity is O(N*log(N)) per test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
#define LL long long
using namespace std;
clock_t start = clock();
LL readInt(LL l, LL r, char endd) {
LL x = 0;
char ch = getchar();
bool first = true, neg = false;
while (true) {
if (ch == endd) {
break;
} else if (ch == '-') {
assert(first);
neg = true;
} else if (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + ch - '0';
} else {
assert(false);
}
first = false;
ch = getchar();
}
if (neg) x = -x;
if (x < l || x > r) {
cerr << l << " " << r << " " << x << " failed\n";
}
assert(l <= x && x <= r);
return x;
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert (g != -1);
if (g == endd) {
break;
}
++cnt;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
LL readIntSp(LL l, LL r) {
return readInt(l, r, ' ');
}
LL readIntLn(LL l, LL r) {
return readInt(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
const int MAX_T = (int)1e6;
const int SUM_N = (int)1e6;
int sum_n, vis[SUM_N];
vector<int> g[SUM_N];
void check_connectivity(int u) {
vis[u] = 1;
for (int v : g[u]) if (!vis[v]) {
check_connectivity(v);
}
}
int du, dv, diameter, lca, par[SUM_N];
pair<int, int> deepest_node[SUM_N];
void find_diameter(int u, int p) {
par[u] = p;
deepest_node[u] = {u, 1};
int mx1 = 0, mx2 = 0, mx1_u = u, mx2_u = u;
for (int v : g[u]) if (v != p) {
find_diameter(v, u);
if (deepest_node[v].second >= mx1) {
mx2 = mx1;
mx2_u = mx1_u;
mx1 = deepest_node[v].second;
mx1_u = deepest_node[v].first;
} else {
if (mx2 < deepest_node[v].second) {
mx2 = deepest_node[v].second;
mx2_u = deepest_node[v].first;
}
}
}
deepest_node[u] = {mx1_u, mx1 + 1};
if (diameter < mx1 + mx2 + 1) {
diameter = mx1 + mx2 + 1;
lca = u;
du = mx1_u;
dv = mx2_u;
}
}
vector<int> height[SUM_N];
void get_depth(int u) {
deepest_node[u] = {u, 1};
vis[u] = 1;
for (int v : g[u]) if (!vis[v]) {
par[v] = u;
get_depth(v);
if (deepest_node[v].second + 1 > deepest_node[u].second) {
deepest_node[u] = {deepest_node[v].first, deepest_node[v].second + 1};
}
}
height[deepest_node[u].second].push_back(u);
}
void solve() {
int n = readIntSp(1, SUM_N);
sum_n += n;
int k = readIntLn(1, n);
for (int i=1;i<=n;++i) {
g[i].clear();
vis[i] = 0;
height[i].clear();
}
for (int i=1;i<n;++i) {
int u = readIntSp(1, n);
int v = readIntLn(1, n);
g[u].push_back(v);
g[v].push_back(u);
}
check_connectivity(1);
for (int i=1;i<=n;++i) {
assert(vis[i]);
vis[i] = 0;
}
if (k == 1) {
cout << "1\n";
return;
}
du = dv = lca = -1;
diameter = 0;
find_diameter(1, 0);
if (k <= diameter) {
cout << "2\n";
return;
}
int u = du;
vector<int> visit_me;
while (u != lca) {
vis[u] = 1;
visit_me.push_back(u);
u = par[u];
}
u = dv;
while (u != lca) {
vis[u] = 1;
visit_me.push_back(u);
u = par[u];
}
vis[lca] = 1;
visit_me.push_back(lca);
for (int u : visit_me) {
for (int i : g[u]) if (!vis[i]) {
par[i] = -1;
get_depth(i);
}
}
for (int i=1;i<=n;++i) vis[i] = 0;
int ans = 2, subtree_size = diameter;
// cout << diameter << " " << du << " " << dv << '\n';
for (int i=n;i>0;--i) {
for (int u : height[i]) if (!vis[u]) {
subtree_size += i;
ans++;
int cur = deepest_node[u].first, taken = 0;
// cout << u << " " << i << " " << cur << " taking\n";
while (cur != -1 && !vis[cur]) {
vis[cur] = 1;
taken++;
cur = par[cur];
}
assert(taken == i);
if (subtree_size >= k) break;
}
if (subtree_size >= k) break;
}
cout << ans << '\n';
}
int main() {
// Start solution here use readIntLn, readIntSp and readStringSp and readStringLn
// for reading input
int T = readIntLn(1, MAX_T);
sum_n = 0;
while (T--) {
solve();
}
// End solution here
assert(1 <= sum_n && sum_n <= SUM_N);
assert(getchar() == EOF);
cerr << fixed << setprecision(10);
cerr << "Time taken = " << (clock() - start) / ((double)CLOCKS_PER_SEC) << " s\n";
return 0;
}
Tester's Solution
#include <iostream>
#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <random>
#ifdef HOME
#include <windows.h>
#endif
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T& a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T& a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x = 0;
int cnt = 0;
int fi = -1;
bool is_neg = false;
while (true) {
char g = getchar();
if (g == '-') {
assert(fi == -1);
is_neg = true;
continue;
}
if ('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if (cnt == 0) {
fi = g - '0';
}
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if (g == endd) {
assert(cnt > 0);
if (is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
}
else {
//assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert(g != -1);
if (g == endd) {
break;
}
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l, r, ' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l, r, '\n');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
int main(int argc, char** argv)
{
#ifdef HOME
if (IsDebuggerPresent())
{
freopen("../SUBTRCOV_2.in", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
int T = readIntLn(1, 1'000'000);
int sumN = 0;
forn(tc, T)
{
int n = readIntSp(1, 1'000'000);
sumN += n;
int k = readIntLn(1, n);
vector<vector<int>> neigh(n);
forn(i, n - 1)
{
int u = readIntSp(1, n);
int v = readIntLn(1, n);
assert(u != v);
--u; --v;
neigh[u].push_back(v);
neigh[v].push_back(u);
}
if (k == 1)
{
printf("1\n");
continue;
}
vector<int> rem(n);
//find root
auto furthest2 = [&](int st) {
vector<tuple<int, int, int>> q(1, { st, -1, 1 });
forn(i, q.size())
{
int act = get<0>(q[i]);
int p = get<1>(q[i]);
int d = get<2>(q[i]);
for (auto cand : neigh[act])
{
if (p != cand && !rem[cand])
{
q.push_back({ cand, act, d + 1 });
}
}
}
return make_pair(get<0>(q.back()), get<2>(q.back()));
};
set<tuple<int, int, int>> s;
auto aa = furthest2(0);
auto bb = furthest2(aa.first);
s.insert({ bb.second, bb.first, aa.first });
vector<int> parent(n);
int ans = 1;
while (k > 0)
{
++ans;
auto best = *s.rbegin();
s.erase(best);
k -= get<0>(best);
int u = get<1>(best);
int v = get<2>(best);
//remove path u,v
{
vector<pair<int, int>> q(1, { u, -1 });
forn(i, q.size())
{
int act = q[i].first;
int p = q[i].second;
for (auto cand : neigh[act])
{
if (!rem[cand] && cand != p)
{
q.push_back({ cand, act });
parent[cand] = act;
}
}
}
}
rem[v] = true;
int actt = v;
while (actt != u)
{
actt = parent[actt];
rem[actt] = true;
}
//collect nodes next to the path which are not removed yet
vector<int> newRoots;
auto collect = [&](int node) {
for (auto cand : neigh[node])
{
if (!rem[cand])
{
newRoots.push_back(cand);
}
}
};
actt = v;
collect(v);
while (actt != u)
{
actt = parent[actt];
collect(actt);
rem[actt] = true;
}
//add the trees to the s
for (auto nr : newRoots)
{
auto nf = furthest2(nr);
s.insert({ nf.second, nr, nf.first });
}
}
printf("%d\n", ans);
}
assert(sumN <= 1'000'000);
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class SUBTRCOV{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), K = ni();
int[] from = new int[N-1], to = new int[N-1];
for(int i = 0; i< N-1; i++){
from[i] = ni()-1;
to[i] = ni()-1;
}
int[][] g = make(N, from, to);
int root = 0;
int[] dist = new int[N];Arrays.fill(dist, 2*N);
dist[0] = 0;
Queue<Integer> q = new LinkedList<>();
q.add(0);
while(!q.isEmpty()){
int u = q.poll();
for(int v:g[u]){
if(dist[v] > dist[u]+1){
dist[v] = dist[u]+1;
q.add(v);
}
}
}
for(int i = 0; i< N; i++)if(dist[i] > dist[root])root = i;
time = -1;
int[] eu = new int[N], st = new int[N], en = new int[N], depth = new int[N], par = new int[N];
dfs(g, par, depth, eu, st, en, root, -1);
LazySegmentTree segmentTree = new LazySegmentTree(N);
for(int i = 0; i< N; i++)segmentTree.update(st[i], st[i], depth[i]);
boolean[] inc = new boolean[N];
inc[root] = true;
int size = 1, ans = 1;
long IINF = (long)1e13;
segmentTree.update(st[root], st[root], -IINF);
while(size < K){
long[] pair = segmentTree.query(0, N-1);
int u = eu[(int)pair[0]];
int add = (int)pair[1];
ans++;
for(int cur = u; !inc[cur]; cur = par[cur]){
size++;
segmentTree.update(st[cur], st[cur], -IINF);
inc[cur] = true;
for(int v:g[cur]){
if(v == par[cur] || inc[v])continue;
segmentTree.update(st[v], en[v], -add);
}
add--;
}
}
pn(ans);
}
int time;
void dfs(int[][] g, int[] par, int[] depth, int[] eu, int[] st, int[] en, int u, int p){
par[u] = p;
eu[++time] = u;
st[u] = time;
for(int v:g[u]){
if(v == p)continue;
depth[v] = depth[u]+1;
dfs(g, par, depth, eu, st, en, v, u);
}
en[u] = time;
}
class LazySegmentTree{
int m = 1;
long IINF = (long)1e18;
long[] t, lazy;
long[] ind;
public LazySegmentTree(int n){
while(m<n)m<<=1;
t = new long[m<<1];
lazy = new long[m<<1];
ind = new long[m<<1];
for(int i = 0; i< m; i++)ind[m+i] = i;
for(int i = m-1; i> 0; i--)
ind[i] = t[i<<1] <= t[i<<1|1]?ind[i<<1]:ind[i<<1|1];
}
private void push(int i, int ll, int rr){
if(lazy[i] != 0){
t[i] += lazy[i];
if(i < m){
lazy[i<<1] += lazy[i];
lazy[i<<1|1] += lazy[i];
}
lazy[i] = 0;
}
}
public void update(int l, int r, long x){u(l, r, 0, m-1, 1, x);}
public long[] query(int l, int r){return q(l, r, 0, m-1, 1);}
public long max(int l, int r){return query(l, r)[1];}
public int argmax(int l, int r){return (int)query(l, r)[0];}
private void u(int l, int r, int ll, int rr, int i, long x){
push(i, ll, rr);
if(l == ll && r == rr){
lazy[i] += x;
push(i, ll, rr);return;
}
int mid = (ll+rr)/2;
if(r <= mid){
u(l, r, ll, mid, i<<1, x);
push(i<<1|1, mid+1, rr);
}else if(l > mid){
push(i<<1, ll, mid);
u(l, r, mid+1, rr, i<<1|1, x);
}else{
u(l, mid, ll, mid, i<<1, x);
u(mid+1, r, mid+1, rr, i<<1|1, x);
}
t[i] = Math.max(t[i<<1], t[i<<1|1]);
if(t[i] == t[i<<1])ind[i] = ind[i<<1];
if(t[i] == t[i<<1|1])ind[i] = ind[i<<1|1];
}
private long[] q(int l, int r, int ll, int rr, int i){
if(l == ll && r == rr)return new long[]{ind[i], t[i]};
int mid = (ll+rr)>>1;
if(r <= mid)return q(l, r, ll, mid, i<<1);
if(l > mid)return q(l, r, mid+1, rr, i<<1|1);
long[] p1 = q(l, mid, ll, mid, i<<1), p2 = q(mid+1, r, mid+1, rr, i<<1|1);
if(p1[1] >= p2[1])return p1;
return p2;
}
}
int[][] make(int N, int[] from, int[] to){
int[] cnt = new int[N];
for(int x:from)cnt[x]++;
for(int x:to)cnt[x]++;
int[][] g = new int[N][];
for(int i = 0; i< N; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< N-1; i++){
g[from[i]][--cnt[from[i]]] = to[i];
g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new SUBTRCOV().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()