Subtree size calculation using BFS (Graph problem 2)

general
, , ,
1

I want to calculate Subtree size (for each vertex ) , of a given graph I know how to do with DFS but how can i implement using BFS ?

Iterative BFS/DFS - Codeforces
I also visit this above link , but unable to implement , I wanna do something with parent but how ? Please help @galencolin @carre @waqar_ahmad224 @hetp111

// DFS implementation
lli SubtreeSize_DFS(lli source , vi adj[] , bool* vis , lli* subtree_size){
    vis[source] = 1;
    lli crsize = 1;
    for(auto xt : adj[source]){
        if(!vis[xt])
            crsize += SubtreeSize_DFS(xt,adj,vis,subtree_size);
    }
    subtree_size[source] = crsize;
    return crsize;
}

//BFS implementataion (complete this )

void SubtreeSize_BFS(bool vis[], lli dist[], lli parent[] , lli s , lli* subtree_size){
    queue<lli>q;
    q.push(s);
    vis[s]=1;
    dist[s]=0;
    parent[s] = s;
    lli cnt=0;
    while(q.empty()==false){

        lli x = q.front();
        q.pop();
        for(auto xt : adj[x])
            {
                if(!vis[xt])
                {
                    dist[xt] = dist[x]+1;
                    vis[xt]=1;
                    q.push(xt);
                    parent[xt] = x;
                }
            }
    }
}
2

First calculate the number of nodes of each node. As in the code, simple recursively calculate the number of nodes by counting the children in each edge.

1 Like
3

For each node I have to backtrack to its parent and store count in the parent it will be N2

4

In above link one user said this but how can i implement - ?

Screenshot_2020-07-01 Iterative BFS DFS - Codeforces
Screenshot_2020-07-01 Iterative BFS DFS - Codeforces903×493 65.4 KB

5
6

Once you have the parents and depth of all nodes using BFS, start from maximum depth(N in worst case), for each node at depth ‘d’, do sz[par[node]]+=sz[node]…iterate from maximum depth to depth = 1…I guess this clears your doubt??

1 Like
7

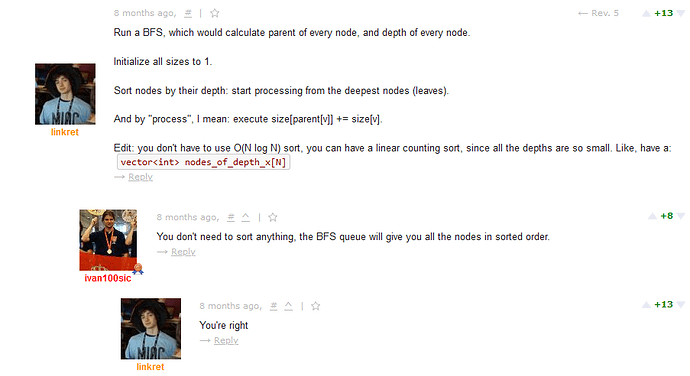
Het I know iterative DFS , but question is how to find with BFS and parent array as one user said this (see pic)

2 Likes
8

Can u write code , it will more understable for me ( as same thing is said by other user but unable to implement that’s why i m asking here :slight_smile: ) , U can edit in my BFS implementation

9

See if this helps:

10

Tell me a thing Basically if we use DFS complexity is (E + V ) when we use BFS still (E+V) or ?

11

It’s O(E+V) in both cases…

1 Like
12

Isn’t time complexity is O( V * ( Number of nodes at depth ‘D’) ?

13

Why??

14 
for(int i=n-1;i>0;i--)
        for(auto j : nodes[i])
            sz[par[j]]+=sz[j];

Outer loops N (means total vertex V) , and inner loop iteraters for all those nodes which are at depth ’ i ’

15

You are analyzing this loop in a wrong way, the total complexity would be O(sum of number nodes at depth ‘d’, d = 1 to n-1) which is equal to ‘n’ since you have ‘n’ nodes in total and therefore overall complexity of this loop is O(n)…is it clear now??

1 Like
16

Overall Complexity is V+E right same as BFS :slight_smile: … Thanks man ,
can u suggest me some set of question in which This Subtree size calculation is used :slight_smile:

17

Even though you’ve found a solution, what’s the point of doing it with BFS?

1 Like
18

Just a thought :slight_smile: . . in cf blog the user said if number of nodes is105 then it will be TLE so i want an iterative approach…

Can u share some questions so that i will practice on this topic :slight_smile:

19

I think you misunderstood the blog. The only issue with DFS was that there would possibly be a stack overflow error. But that would only happen for weaker languages like Python (not C++), and even then, there are very easy ways to get around that.

Also, to get practice problems, just search “trees” as a problem tag on CF and determine if subtree sizes would be useful for each one

2 Likes
20

Ok thanks :slight_smile: . . . My mistake