Hello community, In the march starter contest there was a problem by the name of Server Trouble. I couldn’t do it into the contest. First I thought there would be some sort of binary search in it, but I was wrong. It was simple 4-5 line of code.
But I’m still not getting the approach at all.
Can someone help me getting the approach. How to actually think about the solution.
This is the problem link:
SVRT
Yes I checked the editorial…and also watched the youtube tutorial. but still I’m not satisfied. If you can make the words simple, can you please write the approach in your words, if I get it, that would be amazing…
I know this could be very easy for you…but I have just started cp few months ago.
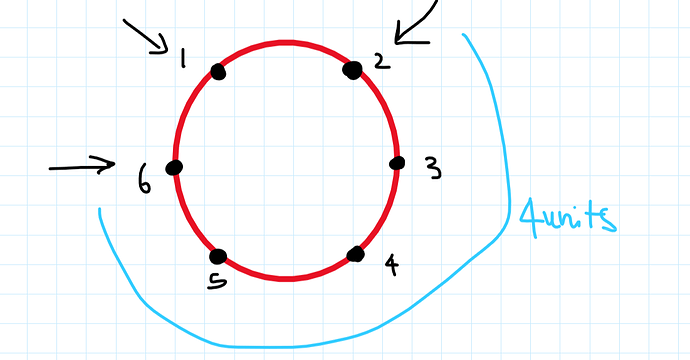
Okay, I’ll try. So the problem asks us to place K servers out of the given N locations such that the maximum distance between any 2 servers can be minimized. Let’s see what the problem looks like for K=3 and N=6. Since the locations 1 and N are adjacent. So we can visualize the setting as a circle and we need to choose any 3 points to put the servers on.
Reference
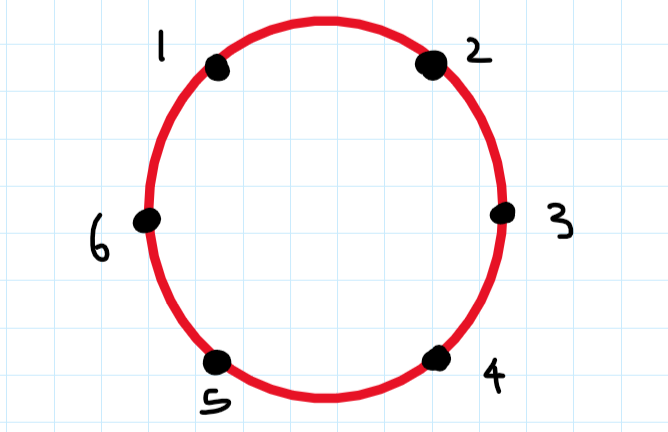
Let’s see what options do we have.
- If we choose point 6,1 and 2 then maximum distance would be 4 (max(1,1,4)).
- Similarly If we choose point 6,1 and 3 then maximum distance would be 3 (max(1,2,3)).
- But if we choose points 6,2 and 4 then maximum distance would be 2 = max(2,2,2).
So from the above analysis, we get an intuition that may be dividing the circle into K equal parts is a good idea. And it is the case because if we try to reduce the distance between any two servers then we actually end up increasing the distance between some pair of servers because of the circular nature of the problem.
So we just reduced the problem to dividing N into K parts which are as equal as possible. Now let’s do some casework.
CASE1: N%k=0:
- It’s the case that we saw just now. And it is clearly evident that maximum distance could be made N/K (6/3=2)for all the K (3) adjacent pairs.
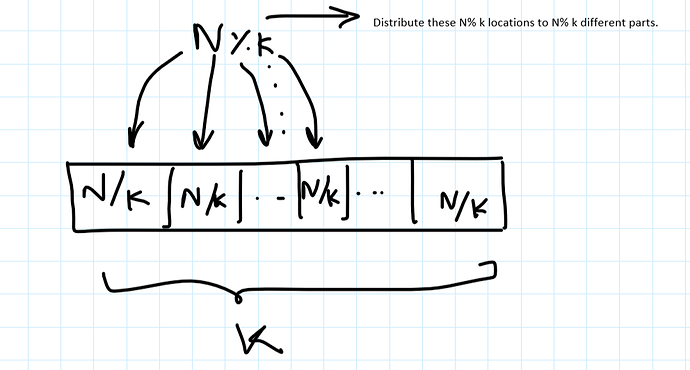
CASE2: N%k !=0 :
- So firstly we can always give N/K to the K parts which we are aiming for. And now we will be left with a residual amount of N%K. And since it will obviously less than K we can simply give all of the N%K locations to N%K different parts thus increasing their count by 1. So Maximum distance would be max(N/K+1,N/K) which is N/K+1 and N%K pairs would have this distance.
Tell me if there is anything in particular which you weren’t able to understand.
I really am not so good at explaining but in that question you were supposed to make a combination of arrangement that would give us minimum of all the maximum distance of adjacent servers.A bit of observation was required for that. The best way of approaching this kind of problems would be to start brute forcing some examples with your pen and paper and see the patterns and then generate a brute force code for it. Soon you will be able to generate a O(1) solution for it (basically a mathematical formula) . Here is my brute force code that I used to see the pattern.
int main(){
speedUP();
int t; cin >> t;
while(t--){
int n, k; cin >> n >> k;
ll d = ceil(n,k);
// ll x = d, y = d-1, ans = -1;
// for(int i = 1; i <= k; i++){
// if( (x * i) + (y * (k - i) ) == n){
// ans = i;
// break;
// }
// }
ll tmp = n % k;
if(tmp == 0){
tmp = k;
}
print(d,tmp);
}
}
I hope this could help a bit!
Eg: 15 6
place servers at 1 4 7 10 12 14 ~ the distance between adjacent pairs was 3 , 3 ,3, 2 , 2 , 2 . This gave me the idea to find the arrangement using brute force
I got it now…actually the problem happening with me was understanding the second case…but now I got it. previously I was not getting residual N%K part…but now I understood it when I read it and try it by myself.
Thanks man, I really appreciate your effort and time to make me understand this…this would really motivate me.
got it…thanks man.
You explained the approach and solution really well, but
and N%K pairs would have this distance.
(Case 2)
How do you figure this out? How did you deduced that N % K pairs would have that maximum distance?
I hope you got the reduced problem (tell me if you didn’t). We only need to divide N into K parts. And each part can be visualized as a pair. So we just need to count the number of parts that have this 1 extra location.
thus increasing their count by 1
I didn’t understand this part…why will it be increased by 1?
Since you’re giving N%k different items to N%k different parts so you’ll increase the count of each part by one as each cell receives exactly one location