TARITAR - EDITORIAL

[taran_1407]

PROBLEM LINK:

Practice
Contest

Setter: Abhishek Pandey
Tester: Taranpreet Singh
Editorialist: This person

DIFFICULTY:

Easy

PREREQUISITES:

Basic Trees, Path, DFS would do the trick.Understanding of Euler tree tour or Binary Lifting would be helpful.

PROBLEM:

Given a tree and location of Tarini X, find if shop P lies in path of Taran T and X.

VARIOUS SOLUTIONS

•   Root the tree on $X$ and just check whether Node $T$ lies in subtree of node $P$ using euler tree tour.
  

•   Root the tree on $X$ and check if $P$ is an ancestor of $T$ using binary Lifting.
  

EXPLANATION

Since we have a node given, rooting the tree can significantly reduce complexity of our solution.

Suppose we have rooted the tree at some node other than X. Let LCA of X and T be L, then our problem is to find whether P lies on path X to L or P lies on path L to T. If either is positive, answer is true.

Just by rooting the tree at X, we reduced above problem to checking if P lies on path of X to T as LCA (root,T) is root.

Now,
Euler Tour Tree Solution

Euler tour can be defined as the tour of tree in a DFS manner, so as to flatten the tree into an array.

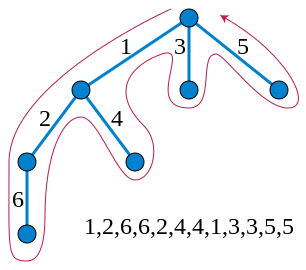
The notable properties of this ordering is that,

• Each vertex is visited exactly twice, one time during entering, and once during leaving.
• Each vertex has a corresponding interval, ranging between entry time ans exit time.
• **Node X is in subtree of node Y if Node Y is entered before Node X and X is left before Node Y. Formally, if st[] denote start time and en[] denote end time, then node X is chid of Node Y is st[Y]<= st[X] and en[X] <= en[Y].

This is all we need to solve this problem using euler tour. Just run a dfs to compute st and en array, thus answering subtree queryies in O(1).

Binary Lifting Solution

We now view the problem in a different manner. Root the tree at X and we need to check if node P is an ancestor of node X.

This a standard binary lifting problem and can be solved as explained by following cases, D[X] denote depth of Node X.

• If D[P] >D[T] ans is NO.
• Else Find ancestor of Node T at same depth as P. If P is that ancestor, answer is YES, else answer is NO.

Bonus Problem

Solve same problem, but X varies with each query.

Complexity:
Euler Tour solution: Precomputation O(N), O(1) per query.
Binary Lifting soluton: Precomputation O(N), O(logN) per query.

AUTHOR’S AND TESTER’S SOLUTIONS:

Setter’s solution
Tester’s solution

Feel free to share your solution or ask any doubts.

PS:There doesn’t exist any person called Tarini, except in mind of Setter.

[vijju123]

Analysis of Contestant’s Solutions-

This problem was a lot of fun to watch. When we proposed it, I intended it to be second easiest problem of the set, solved by almost everyone at least for 40 points.

This problem was especially fun to watch, because when submissions to this problem started happening, me and @taran_1407 were rooting who would be at rank #1 in the contest. At that time, @allllekssssa had solved both of taran’s problems (the third and fourth hardest ones!) along with Terrible Implementation while @meooow was yet to solve the hardest problem. Naturally, taran felt @allllekssssa stood a very good chance (he especially had shown to be good at solving observation/constructive problems as seen in his recent LTIME and COOKOFF set), while I was rooting for my favorite co-mod and the most powerful cat-man/Shatki-Billi our one and only @meooow XD. Now that the contest is over, I can say both of their solutions could be improved . @meooow used LCA (I think) while @allllekssssa also did that using Sparse table if I interpretted his solution right. Both were at least two times more complex than intended one :p.

The problem’s intuition was simple, and there lied its beauty. If you take the tree rooted at 1 like you do for all the other problems, you’d feel its a question of LCA and will probably need some dp and binary lifting to solve. But root the tree at X, and you see that question reduces to checking if a node is in sub-tree of another. Which is simple DFS + Euler Tour.

However, very very VERY few people did it in O(N), most used LCA and Binary Lifting. The first solution I saw using Euler Tour was @dhruvsomani , but he was getting TLE for all the test cases. I wondered why and then noticed he didnt clear the adjacency list after each test case . Not only him, many other, especially div1 coders did henious mistakes like forgetting resetting the counter variable of euler tour, not clearing the list after each test cases, NOT CLEARING VISITED ARRAY EACH TEST CASE. LOL XD. At that time I felt how the leaderboard would be if we used no-feedback system like topcoder where you just submit and you get to know if your solution is correct or not only after contest. XD.

That being said, not many people obtained 40 for this problem, and for a very silly reason. The subtask #2 was designed such that tree has height O(LogN), making brute force answer query in O(LogN). But even in brute fore, many people faced problem. The intended brute force was, take the node of Taran, or Tarini, whichever is at greater depth, move up by 1, see if there is a shop there or not, and if they met or not. But people used DFS (got WA when shop was in not in path of taran to tarini but near taran anyway). Then, some people who got the brute force right, were able to fetch only 20, why? Slow input and Slow output!

Setter’s solution, when tested on testing page, with fast input-output, took 0.36 seconds. Seeing that, a time limit of 1 or 1.5 seconds would have been quite reasonable. But it turns out, many coders, even div1, forgot that there is a huge input and a HUGE output to print! One has to read and print \approx {10}^6 numbers for larger files, which takes quite a lot of time. O(N) solutions using Euler Tour with slow output did it in 1.45 seconds while with slow input and output, they got TLE. And I feel its good, unrated contest is the best place to learn such lessons. BTW, how many of you noticed in statement of TIMPLEM that “Give them so many intervals that they get TLE in I/O operations itself!”. Well, surprise, it applies for this problem! XD. It was a hidden hint, I just threw Fast I/O there so that it gets in back of your mind, so that when you guys try this problem you guys keep in mind to use it either because of getting TLE, or because you used it in TIMPLEM. (There are at least 5 hidden meanings in each of my statements but lets keep that for some other day XD)

Back to Time Limit, I decided to keep it at 2 seconds also as it gave a bit of scope to any alternative solution, and I feel it went well this time as had the time limit been 1 seconds, many LCA approaches would have failed (esp. because of I/O).

That being said, I hope you guys appreciate the simplicity of the problem. While LCA was the standard way to go, just a little observation and thinking reduced this problem to a very basic one. To all those who were able to see this, whether you got AC or not, doesnt matter, you guys won most of the problem by this. Implementation will follow with practice, getting logic and ideas is the first and most important step to success.

Regards
@vijju123

[anon95832944]

Please give a hint for the bonus