PROBLEM LINK:
Author: Erfan Alimohammadi
Tester: Hussain
Editorialist: Oleksandr Kulkov
DIFFICULTY:
HARD
PREREQUISITES:
Analytic geometry, Mechanics
PROBLEM:
You’re given 2 balls A and B on 2-dimensional plane moving with constant velocities A_v and B_v and having radii A_r and B_r. Also there is a wall from which they might bounce off. You have to calculate the area of the largest possible intersection of these two balls over all moments of time.
QUICK EXPLANATION:
Add “virtual” balls moving on us from the other side of the wall, this reduces our problem to finding moment of time when two moving points have smallest distance between each other, after that use every single formula from computational geometry you can recall to solve the problem.
EXPLANATION:
For convenience we will use STL complex numbers as substitute for point class:
typedef double ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return a.x() * b.x() + a.y() * b.y();
}
ftype cross(point a, point b) {
return a.x() * b.y() - a.y() * b.x();
}
void read(point &r) {
ftype x, y;
cin >> x >> y;
r = {x, y};
}
Let’s solve the problem step by step, from less horrifying parts to more horrifying ones.
Overlapping area. It’s pretty obvious that we need to know the minimum possible distance between centers of two balls. Let’s learn how to calculate area of intersection, given balls radii r_1 and r_2 and distance between their centers d. First of all in case d>r_1+r_2 then intersection is empty and in case d < |r_1-r_2| smallest ball completely lies inside largest, thus answer in this case is \pi \min(r_1,r_2)^2.
Otherwise situation is as follows:
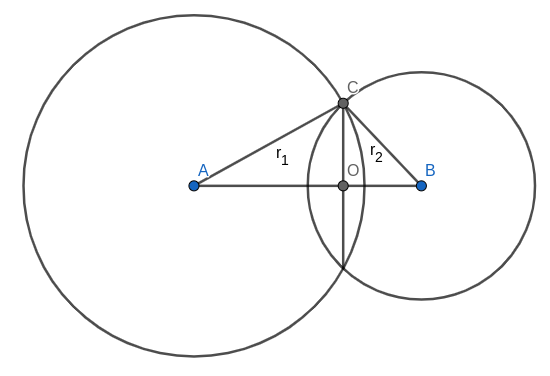
To calculate the area of intersection we have to know AO, we can obtain it from equation:
You’re given r_1=AC, r_2 = BC and d=AB. Let a = AO, then:
Now that we know a we may split the whole calculation in two parts, namely for first circle with parameters (r_1,a) and for second circle with parameters (r_2, d-a):
ftype overlap(ftype r1, ftype r2, ftype d) {
if(d >= r1 + r2) {
return 0;
} else if(d <= abs(r1 - r2)) {
return pi * norm(min(r1, r2));
} else {
ftype a = (norm(r1) - norm(r2) + norm(d)) / (2 * d);
return area(r1, a) + area(r2, d - a);
}
}
Area of circular segment. Now our situation is as follows:
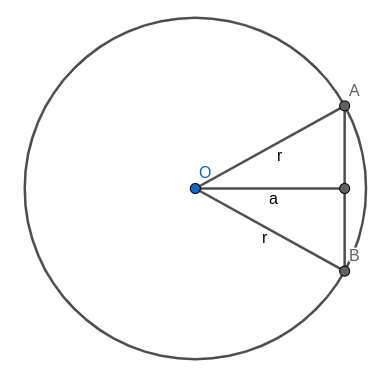
We have to calculate area of circular segment AB, to do this we should subtract area of \triangle OAB from area of circular sector OAB. Let \angle AOB = 2\varphi, then circular sector has area \varphi r^2 and triangle has area a\sqrt{r^2-a^2}. Note that \cos \varphi = \tfrac{a}{r}, thus you should return following value:
ftype area(ftype r, ftype a) {
return norm(r) * acos(a / r) - a * sqrt(norm(r) - norm(a));
}
Note that formula holds even if a\leq 0.
Mirrors and reflections. Consider the movement of ball A when it bounces from the wall:
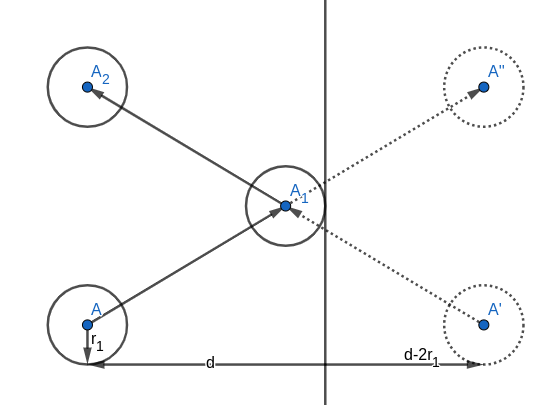
It proves convenient to assume that ball A simply fell behind the wall and continued its movement towards position A'' while at the same time it’s reflection A' ascended from the wall and moved towards A_2 instead of initial ball A. It heavily simplifies problem because it allows us to forget about the wall at all and instead consider four moving balls A,A',B,B'. Closest distance between any ball marked with A or A' and any ball marked with B or B' will provide us with the answer.
Note though that for these intersections you must consider balls which are really presented on our side of the wall. Let A_t be the time to get from A to A_1. Then we deal with ball A on [0,A_t] and with A' on [A_t,+\infty). Note that if A_t < 0 we may say that ball A already bounced from the wall and we actually should consider only movement of ball A.
Now we should carefully replicate the balls and recalculate their velocities. To do this we will consider normal unit vector n to the line L=(W_1,W_2). Distance from A to L has signed length equal to d=(A-W_1) \cdot n and projection of A's velocity on L is V_d = A_v \cdot n. From this we may obtain explicit formulas for A' and A_v':
Also since we know that distance from A_1 to L is A_r, we may say that:
Thus we have following implementation for calculating A, A_v and A_t.
ftype sign(ftype x) {
return x < 0 ? -1 : 1;
}
tuple<point, point, ftype> reflect(point A, point Av, ftype Ar, point W1, point W2) {
point nrm = point(0, 1) * (W2 - W1);
nrm /= abs(nrm);
ftype d = dot(A - W1, nrm);
ftype Vd = dot(Av, nrm);
point A_ = A - 2 * (d - sign(d) * Ar) * nrm;
point Av_ = Av - 2 * Vd * nrm;
if(abs(Vd) < eps || sign(d - sign(d) * Ar) != sign(Vd)) {
return {A, Av, 0};
} else {
ftype At = -(d - sign(d) * Ar) / Vd;
return {A_, Av_, At};
}
}
Closest distance between rays. Now for the final part. We have balls A and B flying in 2D space with velocities A_v and B_v correspondingly. We need to calculate closest distance between them in segment of time [t_l,t_r]. Instead of considering both movements we will say that A doesn’t move at all and B moves with velocity B_v-A_v, then our task now is to find distance from A to the ray which goes from B and has direction B_v.
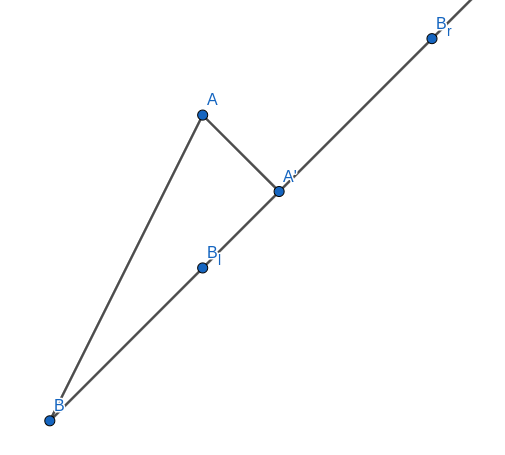
Here BA' = \tfrac{(A-B) \cdot B_v}{|B_v|}, thus it’ll take time t=\tfrac{(A-B)\cdot B_v}{|B_v|^2} to get from B to A'. If t_l \leq t \leq t_r then we should return distance from A to A' which is equal to \tfrac{(A-B)\times B_v}{|B_v|}, otherwise we should return minimum of distances from A to B_l and to B_r:
ftype dist(point A, point Av, point B, point Bv, ftype tl, ftype tr) {
if(tl > tr) {
return inf;
} else {
Bv -= Av;
ftype t = dot(A - B, Bv) / norm(Bv);
if(tl <= t && t <= tr) {
return abs(cross(A - B, Bv)) / abs(Bv);
} else {
return min(abs(A - (B + tl * Bv)), abs(A - (B + tr * Bv)));
}
}
}
Gluing it all together. After we’ve introduced all auxiliaries, solution looks like this:
void solve() {
point A, Av; ftype Ar;
point B, Bv; ftype Br;
read(A); read(Av); cin >> Ar;
read(B); read(Bv); cin >> Br;
point W1, W2;
read(W1); read(W2);
point A_, Av_, B_, Bv_;
ftype At, Bt;
tie(A_, Av_, At) = reflect(A, Av, Ar, W1, W2);
tie(B_, Bv_, Bt) = reflect(B, Bv, Br, W1, W2);
ftype d = min({dist(A, Av, B, Bv, 0, min(At, Bt)),
dist(A_, Av_, B, Bv, At, Bt),
dist(A, Av, B_, Bv_, Bt, At),
dist(A_, Av_, B_, Bv_, max(At, Bt), inf)});
cout << overlap(Ar, Br, d) << "\n";
}
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
Editorialist’s solution can be found here.