PROBLEM LINK:
Practice
Div-3 Contest
Div-2 Contest
Div-1 Contest
Author & Editorialist: Jay Sharma
Tester: Radoslav Dimitrov
DIFFICULTY:
MEDIUM
PREREQUISITES:
Reflected Binary Code (Gray Code)
PROBLEM:
An N\times N grid is filled with two types of 1\times 1 tiles which look like a square with a blue line running across exactly one of its diagonals. The initial configuration is not known. We can ask up to Q queries. In each query, we will provide the coordinates of a cell in the grid. The grader will rotate the tile in that cell by 90^{\circ} and return the number of squares of area 2 unit^2 in the grid formed by the blue diagonal lines only after the rotation. We need to guess the exact configuration of the grid after all the queries.
SOME HINTS:
Hint 1
Apart from getting information about the grid, we can also use the queries to rotate the tile in any arbitrary cell of the grid.
Hint 2
Instead of trying to guess the configuration, let’s try to set the grid to a particular configuration
Hint 3
The constraints for the First Subtask look strange. N\in \{ 2,4\}, why not N=3? Is there anything special about even length grids?
Hint 4
What can you infer from 4\cdot N^{2} queries? You can try all possible combinations for a 2\times 2 grid. So, divide the whole grid into 2\times 2 sub-grids and try to develop some kind of pattern for each of them individually.
Hint 5
Handle the case of odd N separately.
QUICK EXPLANATION:
Instead of guessing the configuration, let’s try to set the grid to a particular configuration. In this solution, I will choose the following end configuration for an even length grid -
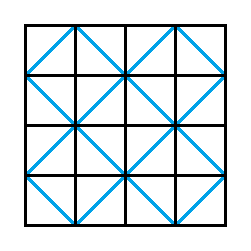
For an odd length grid, there can be many variations. In this solution, I will use the following end configuration -

EXPLANATION:
In this whole explanation, by squares I mean the squares of area 2 unit^2 formed by the blue diagonal lines only.
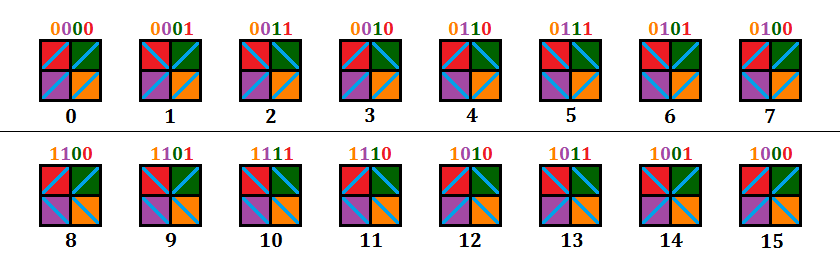
Let us start with the most basic case - the 2\times 2 grid. All possible configurations of the 2\times 2 grid are given below -
Out of all these configurations, the configuration 4 is of our interest since it is the only configuration which contains a square. So, for a 2\times 2 grid, we can generate all the 16 possible configurations and once we receive 1 as the output, we can be sure that the grid is in configuration 4.
How to generate all 16 configurations in just 16 queries
Let’s look again at the 16 configurations for the 2\times 2 grid. Note that each configuration differs from its previous configuration by exactly 1 tile. If we mask the tiles by assigning left-top tile as bit 0, right-top tile as bit 1, left-bottom tile as bit 2 and right-bottom tile as bit 3, then the bitmasks of each configuration will be the one given above it. The sequence we get is the Reflected Binary Code also known as Gray Code. You can read more about it here.
Now, we will extend this idea to any N\times N grid where N is even. Such grids can be perfectly divided into 2\times 2 sub-grids. In this solution, I will refer these sub-grids as blocks and the process of getting the configuration 4 for a block as setting up a block.
First, we will try to set up the blocks on the topmost two rows, then the leftmost two columns and then the rest of the blocks first row-wise and then column-wise.
We can generate all possible configurations for the blocks in a similar way as described above. But now, we need a different way to check whether the block is set or not.
Blocks on topmost rows and leftmost columns:
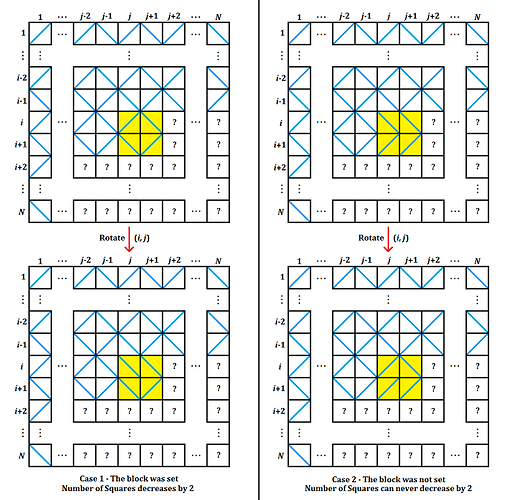
Consider the effect of rotating the top-left tile of a block as given in the image below -
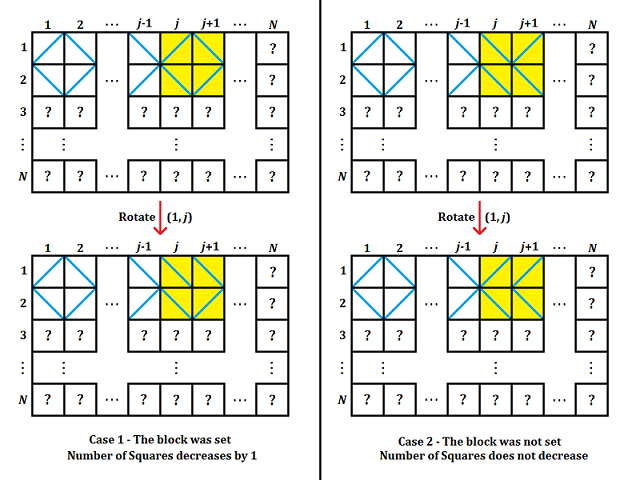
The block under consideration is coloured yellow. If the block was in configuration 4, the rotation decreases the number of squares by 1. If the block was in configuration 5, the rotation increases the number of squares by 1 and changes it to configuration 4. In all other cases, the rotation will not affect the number of squares.
Other blocks:
Once again, consider the effect of rotating the top-left tile of a block as given in the image below -
The block under consideration is coloured yellow. If the block was in configuration 4, the rotation decreases the number of squares by 2. If the block was in configuration 5, the rotation increases the number of squares by 2 and changes it to configuration 4. If the block was in one of the configurations 0,3,7,8,11,12 or 15, the rotation decreases the number of squares by 1. If the block was in one of the configurations 1,2,6,9,10,13 or 14, the rotation increases the number of squares by 1.
Thus, by rotating the top-left tile, we can check whether the block is set or not.
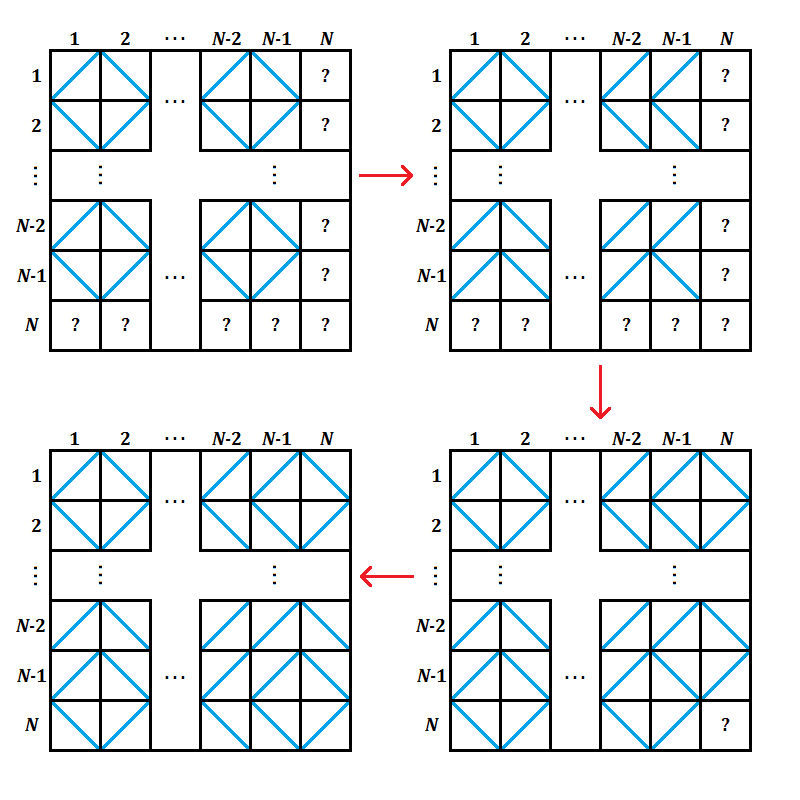
Finally, let us extend our idea to N\times N grids where N is odd. First, we will set up an (N-1)\times (N-1) grid as above. Then, we will invert all the tiles in the second-last row and second-last column except the last ones. Then we will set up the blocks in the last two rows and columns except the bottom-rightmost one. Finally, we will set up the bottom-rightmost block by inverting the tiles in the cells (N-1,N-1), (N-1,N) and (N,N-1) and trying the two configurations for the last cell. The whole process is described in the image below -
SUBTASKS, NUMBER OF QUERIES AND TIME COMPLEXITY:
Subtask 1 - Bruteforce all 2^{N^{2}} configurations using Gray Code. Whenever we receive \frac{(N-1)^{2}+1}{2} from the judge, there is only one possible configuration corresponding to it.
Time Complexity - \mathcal O(2^{N^{2}}) or \mathcal O(N^2\cdot 2^{N^{2}}) depending upon implementation.
Subtask 2 - Let us simply simulate the algorithm described above.
For even N, there will be \frac{N^{2}}{4} blocks. For each block, there are 16 configurations and for checking out each configuration, we need 3 queries, one for flipping the tile required to change the configuration and two for checking if the block is set or not. Thus, in total, we require:
\frac{N^{2}}{4}\times 16\times 3
=12\cdot N^{2} queries.
For odd N, we require 12\cdot (N-1)^{2} queries for setting up the (N-1)\times (N-1) grid, 14\cdot (N-1) queries for setting up the last row and column and 9 queries for setting up the last cell. Thus, in total, we require:
12\cdot (N-1)^{2}+14\cdot (N-1)+9
=12\cdot N^{2}-10\cdot N+7
\leq 12\cdot N^{2} \forall N\geq 2
Time Complexity - \mathcal O(N^{2}).
Subtask 3 - Let us notice one thing. In the Gray Code encoding, we are flipping the top-left tile of a block every alternate move. Instead of checking each configuration separately, we can check two configurations differing in the top-left tile simultaneously. Then, there will be no need to separately flip the top-left tile two times for checking whether the block is set or not. The state of one configuration can now simply be used to check the state of the other. But there may a case when the first configuration was set but the second one was not. In this case, we will require 1 additional query to set it back. Thus, now each block can be set in 17 queries and there are \frac{N^{2}}{4} blocks for even N. For even N, we require:
=\frac{17\cdot N^{2}}{4}
\leq 5\cdot N^{2} \forall N\geq 2
For odd N, after this optimisation, we will require:
\frac{17\cdot (N-1)^{2}}{4}+14\cdot (N-1)+9
=\frac{17\cdot N^{2} + 22\cdot N-3}{4} queries.
Unfortunately, this is > 5\cdot N^{2} for N\in \{3,5,7\}.
To fix this, notice that for the blocks in the last column, we can also use the top-right cell for checking whether the block is set or not. Similarly, we can use the bottom-left cell for blocks in the last row. With this optimisation, the number of queries we will require is:
\frac{17\cdot (N-1)^{2}}{4}+7\cdot (N-1)+5
=\frac{17\cdot N^{2} - 6\cdot N+9}{4}
\leq 5\cdot N^{2} \forall N\geq 2
Time Complexity - \mathcal O(N^{2}).
Subtask 4 - Notice that we just need to eliminate 1 query per block from the solution for Subtask 3 to get to the final solution. Till now, we had been considering all blocks independently. But in fact, we can eliminate the first query for every block by simply using the last query from the previous block. For the first block, we can use the initial number of squares given as an initial input. Alternatively, we can leave the block in configuration 5 and set a flag bit for the block meaning that the top-left cell of that block is flipped. This will save us one query per block but will require unnecessary storage and will also destroy the beauty of the final configuration of the grid. So, I prefer using the first optimisation.
Now, for even N, we will require:
16\times \frac{N^{2}}{4}
=4\cdot N^{2} queries.
For odd N, we will require:
4\cdot (N-1)^{2}+5\cdot (N-1)+5
=4\cdot N^{2}-3\cdot N+4 queries
\leq 4\cdot N^{2} \forall N\geq 2
Time Complexity - \mathcal O(N^{2}).
SOLUTIONS:
Setter's Solution (in C++)
/*Problem - Guess The Tiling
*Author - Jay Sharma (jay_1048576)
*/
#include <bits/stdc++.h>
using namespace std;
/*This is the order in which cells must be rotated in order to generate all possible combinations.
*It follows the Gray Code Scheme
*/
pair<int,int> transition[] = {{1,1},{1,0},{1,1},{0,1},{1,1},{1,0},{1,1}};
//Similar to the transition array, this is used to adjust the last row and colunmn only
int transition2[] = {1,0,1};
int query(int i,int j)
{
int x;
cout << 1 << " " << i << " " << j << endl;
cin >> x;
return x;
}
void print(int i,int j,int k)
{
if(((i+j)%2)==k)
cout << 0 << " ";
else
cout << 1 << " ";
}
/*Function to adjust each 2x2 block except probably the last row or column.
*Requires atmost 16 queries per 4 cells
*/
int adjust2x2(int i,int j,int step,int prev)
{
int x,y;
x=query(i,j);
if(x==prev-step)
{
x=query(i,j);
return prev;
}
else if(x==prev+step)
return x;
else
{
int k=0;
while(true)
{
x=query(i+transition[k].first,j+transition[k].second);
y=query(i,j);
if(x==y-step)
return y;
else if(x==y+step)
{
y=query(i,j);
return x;
}
else
k++;
}
}
}
//Function to adjust the blocks of the last row ignoring the top right cell of the block
int adjustEndRowIgnore(int n,int j,int prev)
{
int x,y;
y=query(n-1,j+1);
if(y==prev+1)
return y;
else
{
int k=0;
while(true)
{
x=query(n,j+1+transition2[k]);
if(x==y+1)
return x;
else
k++;
}
}
}
/*Function to adjust the blocks of the last row considering the top right cell.
*Requires atmost 5 queries per 2 cells
*/
int adjustEndRow(int n,int j)
{
int x=query(n-1,j+2);
return adjustEndRowIgnore(n,j,x);
}
/*Function to adjust the blocks of the last column.
*Requires atmost 5 queries per 2 cells
*/
int adjustEndCol(int n,int i)
{
int x=query(i+2,n-1);
int y=query(i+1,n-1);
if(y==x+1)
return y;
else
{
int k=0;
while(true)
{
x=query(i+1+transition2[k],n);
if(x==y+1)
return x;
else
k++;
}
}
}
/*Function to adjust the right bottom corner block
*Requires atmost 5 queries for just the last cell
*But the extra query is always compensated for by the above 2 functions
*/
int adjustCorner(int n)
{
int x=query(n-1,n-1);
x=query(n,n-1);
x=query(n-1,n);
int y=query(n,n);
if(x>y)
return query(n,n);
else
return y;
}
int adjustEvenGrid(int n,int prev)
{
for(int j=0;j<n;j+=2)
prev=adjust2x2(1,j+1,1,prev);
for(int i=2;i<n;i+=2)
prev=adjust2x2(i+1,1,1,prev);
for(int i=2;i<n;i+=2)
for(int j=2;j<n;j+=2)
prev=adjust2x2(i+1,j+1,2,prev);
return prev;
}
int adjustOddGrid(int n,int prev)
{
prev=adjustEvenGrid(n-1,prev);
for(int i=0;i<n-1;i+=2)
prev=adjustEndCol(n,i);
for(int j=0;j<n-3;j+=2)
prev=adjustEndRow(n,j);
prev=adjustEndRowIgnore(n,n-3,prev);
return adjustCorner(n);
}
int main()
{
int tc;
cin >> tc;
while(tc--)
{
int n,q,prev;
cin >> n >> q >> prev;
if(n%2==0)
{
prev=adjustEvenGrid(n,prev);
cout << 2 << endl;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
print(i,j,0);
cout << endl;
}
}
else
{
prev=adjustOddGrid(n,prev);
cout << 2 << endl;
for(int i=0;i<n-2;i++)
{
for(int j=0;j<n-2;j++)
print(i,j,0);
for(int j=n-2;j<n;j++)
print(i,j,1);
cout << endl;
}
for(int i=n-2;i<n;i++)
{
for(int j=0;j<n-2;j++)
print(i,j,1);
for(int j=n-2;j<n;j++)
print(i,j,0);
cout << endl;
}
}
int verdict;
cin >> verdict;
if(verdict==-1)
return 0;
}
return 0;
}
Setter's Solution (in Java)
/**Problem - Guess The Tiling
*Author - Jay Sharma (jay_1048576)
*/
import java.util.Scanner;
class TILESQRS
{
/*This is the order in which cells must be rotated in order to generate all possible combinations.
*It follows the Gray Code Scheme
*/
static int transition[][] = {{1,1},{1,0},{1,1},{0,1},{1,1},{1,0},{1,1}};
//Similar to the transition array, this is used to adjust the last row and colunmn only
static int transition2[] = {1,0,1};
static Scanner in = new Scanner(System.in);
static int query(int i,int j)
{
int x;
System.out.println("1 "+i+" "+j);
System.out.flush();
x = in.nextInt();
return x;
}
static void print(int i,int j,int k)
{
if(((i+j)%2)==k)
System.out.print("0 ");
else
System.out.print("1 ");
}
/*Function to adjust each 2x2 block except probably the last row or column.
*Requires atmost 16 queries per 4 cells
*/
static int adjust2x2(int i,int j,int step,int prev)
{
int x,y;
x=query(i,j);
if(x==prev-step)
{
x=query(i,j);
return prev;
}
else if(x==prev+step)
return x;
else
{
int k=0;
while(true)
{
x=query(i+transition[k][0],j+transition[k][1]);
y=query(i,j);
if(x==y-step)
return y;
else if(x==y+step)
{
y=query(i,j);
return x;
}
else
k++;
}
}
}
//Function to adjust the blocks of the last row ignoring the top right cell of the block
static int adjustEndRowIgnore(int n,int j,int prev)
{
int x,y;
y=query(n-1,j+1);
if(y==prev+1)
return y;
else
{
int k=0;
while(true)
{
x=query(n,j+1+transition2[k]);
if(x==y+1)
return x;
else
k++;
}
}
}
/*Function to adjust the blocks of the last row considering the top right cell.
*Requires atmost 5 queries per 2 cells
*/
static int adjustEndRow(int n,int j)
{
int x=query(n-1,j+2);
return adjustEndRowIgnore(n,j,x);
}
/*Function to adjust the blocks of the last column.
*Requires atmost 5 queries per 2 cells
*/
static int adjustEndCol(int n,int i)
{
int x=query(i+2,n-1);
int y=query(i+1,n-1);
if(y==x+1)
return y;
else
{
int k=0;
while(true)
{
x=query(i+1+transition2[k],n);
if(x==y+1)
return x;
else
k++;
}
}
}
/*Function to adjust the right bottom corner block
*Requires atmost 5 queries for just the last cell
*But the extra query is always compensated for by the above 2 functions
*/
static int adjustCorner(int n)
{
int x=query(n-1,n-1);
x=query(n,n-1);
x=query(n-1,n);
int y=query(n,n);
if(x>y)
return query(n,n);
else
return y;
}
static int adjustEvenGrid(int n,int prev)
{
for(int j=0;j<n;j+=2)
prev=adjust2x2(1,j+1,1,prev);
for(int i=2;i<n;i+=2)
prev=adjust2x2(i+1,1,1,prev);
for(int i=2;i<n;i+=2)
for(int j=2;j<n;j+=2)
prev=adjust2x2(i+1,j+1,2,prev);
return prev;
}
static int adjustOddGrid(int n,int prev)
{
prev=adjustEvenGrid(n-1,prev);
for(int i=0;i<n-1;i+=2)
prev=adjustEndCol(n,i);
for(int j=0;j<n-3;j+=2)
prev=adjustEndRow(n,j);
prev=adjustEndRowIgnore(n,n-3,prev);
return adjustCorner(n);
}
public static void main(String args[])
{
int tc;
tc = in.nextInt();
while(tc-->0)
{
int n,q,prev;
n = in.nextInt();
q = in.nextInt();
prev = in.nextInt();
if(n%2==0)
{
prev=adjustEvenGrid(n,prev);
System.out.println("2");
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
print(i,j,0);
System.out.println();
}
System.out.flush();
}
else
{
prev=adjustOddGrid(n,prev);
System.out.println("2");
for(int i=0;i<n-2;i++)
{
for(int j=0;j<n-2;j++)
print(i,j,0);
for(int j=n-2;j<n;j++)
print(i,j,1);
System.out.println();
}
for(int i=n-2;i<n;i++)
{
for(int j=0;j<n-2;j++)
print(i,j,1);
for(int j=n-2;j<n;j++)
print(i,j,0);
System.out.println();
}
System.out.flush();
}
int verdict;
verdict = in.nextInt();
if(verdict==-1)
System.exit(0);
}
}
}
Tester's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (1 << 10);
int n, q, k;
vector<int> order = {0, 1, 3, 2, 6, 7, 5, 4};
array<int, 3> dx = {0, 1, 1}, dy = {1, 0, 1};
class QueryHandler {
private:
int K, Q;
public:
QueryHandler(int initial_K, int max_Q) {
K = initial_K;
Q = max_Q;
}
int query(int x, int y) {
assert(Q > 0);
int new_K, delta;
cout << 1 << " " << x + 1 << " " << y + 1 << endl << flush;
cin >> new_K;
delta = new_K - K;
K = new_K;
Q--;
return delta;
}
};
void fix(int x, int y, int need, QueryHandler &handler) {
int last = 0;
for(int c: order) {
int diff = c ^ last;
last = c;
for(int i = 0; i < 3; i++) {
if(diff & (1 << i)) {
handler.query(x + dx[i], y + dy[i]);
}
}
int delta = handler.query(x, y);
if(delta == need) {
return;
} else if(delta == -need) {
assert(handler.query(x, y) == need);
return;
}
}
}
void read() {
cin >> n >> q >> k;
}
void solve() {
QueryHandler handler(k, q);
for(int row = 0, delta_ur; row < n - 1; row += 2) {
for(int col = 0; col < n - 1; col += 2) {
fix(row, col, 1 + (int)(col > 0 && row > 0), handler);
}
if(n % 2 == 1) {
handler.query(row, n - 2);
handler.query(row + 1, n - 2);
delta_ur = handler.query(row, n - 1);
if(delta_ur == 1) {
continue;
} else if(delta_ur == -1) {
assert(handler.query(row, n - 1) == 1);
continue;
}
// change dr
handler.query(row + 1, n - 1);
delta_ur = handler.query(row, n - 1);
if(delta_ur == 1) {
continue;
} else if(delta_ur == -1) {
assert(handler.query(row, n - 1) == 1);
continue;
}
assert(false);
}
}
if(n % 2 == 1) {
// fix last row and col
for(int col = 0, delta_dl; col < n - 1; col += 2) {
handler.query(n - 2, col);
if(col != n - 3) {
handler.query(n - 2, col + 1);
}
delta_dl = handler.query(n - 1, col);
if(delta_dl == 1) {
continue;
} else if(delta_dl == -1) {
assert(handler.query(n - 1, col) == 1);
continue;
}
// change dr
handler.query(n - 1, col + 1);
delta_dl = handler.query(n - 1, col);
if(delta_dl == 1) {
continue;
} else if(delta_dl == -1) {
assert(handler.query(n - 1, col) == 1);
continue;
}
assert(false);
}
handler.query(n - 1, n - 2);
handler.query(n - 2, n - 2);
handler.query(n - 2, n - 1);
if(handler.query(n - 1, n - 1) != 1) {
assert(handler.query(n - 1, n - 1) == 1);
}
}
cout << 2 << endl << flush;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
int ret = i + j + (int)(i >= n - 2 && n % 2) + (int)(j >= n - 2 && n % 2);
cout << ret % 2 << " ";
}
cout << endl << flush;
}
int resp;
cin >> resp;
assert(resp == 1);
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while(T--) {
read();
solve();
}
return 0;
}
VIDEO EDITORIAL:
If you have a different approach, feel free to share it below even if it passes only some subtasks. And as always, doubts are welcome ![]()