PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Deepak Prajapati
Tester: Istvan Nagy
Editorialist: Taranpreet Singh
DIFFICULTY
Cakewalk
PREREQUISITES
None, prefix sums might be helpful.
PROBLEM
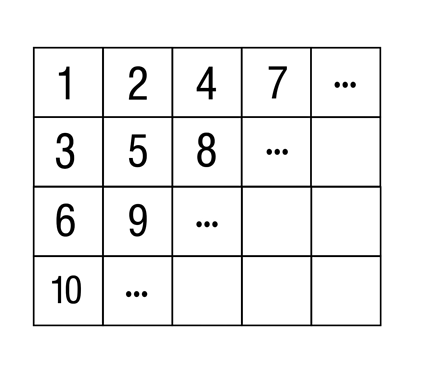
Given an infinite matrix, whose values are filled in the following manner.
Among all paths from cell (x_1, y_1) to (x_2, y_2) by only moving right or down, find the value of the path with maximum value, where the value of a path is the sum of values of cells on the path including starting and ending cell.
QUICK EXPLANATION
- The optimal path is to move downwards from (x_1, y_1) to (x_2, y_1) and then from (x_2, y_1) to (x_2, y_2).
- The values of vertical and horizontal paths can be computed by precomputing the prefix sums of each row and column.
EXPLANATION
Assume we have already generated the matrix, V_{i, j} denoting the value of cell (i, j).
Figuring out Optimal Path
Let’s figure out how this matrix is generated. The values are filled diagonal-wise, and each diagonal is filled from top to bottom. We are going to use the second fact.
1 2 4 7 11
3 5 8 12
6 9 13
10 14
15
Let’s consider a path from cell (1, 1) to cell (3, 3) and consider all paths.
- (1,1) -> (1, 2) -> (1, 3) -> (2, 3) -> (3, 3) with value 28
- (1,1) -> (1, 2) -> (2, 2) -> (2, 3) -> (3, 3) with value 29
- (1,1) -> (1, 2) -> (2, 2) -> (3, 2) -> (3, 3) with value 30
- (1,1) -> (2, 1) -> (2, 2) -> (2, 3) -> (3, 3) with value 30
- (1,1) -> (2, 1) -> (2, 2) -> (3, 2) -> (3, 3) with value 31
- (1,1) -> (2, 1) -> (3, 1) -> (3, 2) -> (3, 3) with value 32
As you may already have guessed, the optimal path moves all downward moves first, and then all right moves.
Let’s denote the sequence of moves by characters ‘R’ denoting the right move and ‘D’ denoting the downward move.
Claim: In optimal move sequence, there are no two consecutive moves where the first move is a right move and the second move is a down move. That means, RD doesn’t appear in the move sequence.
Proof: Let’s assume we are at cell (x, y) and the next two moves are RD in this order. The path would look like (x, y) -> (x, y+1) -> (x+1, y+1). We can see that we can replace this sequence with DR, resulting in path (x, y) -> (x+1, y) -> (x+1, y+1). Let’s compare their values.
Cell (x, y) and (x+1, y+1) appear in both sequences, so their weight doesn’t matter. We only need to compare V_{x, y+1} and V_{x+1, y}. As a matter of fact, they lie on the same diagonal. Specifically, while constructing matrix, cell (x, y+1) is filled first, immediately followed by cell (x+1, y). Hence, the V_{x+1, y} = 1+V_{x, y+1}
Hence, in the move sequence, if there appears any occurrence of moves RD, we can swap moves to obtain DR. We keep doing this until there’s no occurrence of RD in the move sequence. The move sequence becomes DDD \ldots DDRR \ldots RR, all down moves followed by all right moves.
Computing the value of the path
Constraints are small enough to iterate moving from cell (x_1, y_1) to (x_2, y_1) and then to (x_2, y_2) and adding up their values. Setter’s solution does this.
Alternatively, you may use prefix sums for each row and column to answer test cases in O(1) time. You may read more on prefix sums here, or refer to my implementation below.
Implementation Error to avoid: Generate the matrix of size 2000 instead of 1000, since value at cell (1000, 1000) is impacted by cells outside 1000*1000 matrix.
TIME COMPLEXITY
The time complexity is O(MAX^2+T) or O(MAX^2+T*MAX) where MAX = 2000 depending upon implementation.
SOLUTIONS
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
int matrix[1005][1005];
void infiniteMatrix()
{
for(int i = 1; i <= 1000; i++)
{
matrix[i][1] = i * (i+1)/2;
for(int j = 2; j <= 1000; j++)
{
matrix[i][j] = matrix[i][j-1] + (j - 1) + (i - 1);
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
infiniteMatrix();
int t;
cin >> t;
while(t--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
int sum = 0;
for(int i = x1; i <= x2; i++)
{
sum += matrix[i][y1];
}
for(int i = y1+1; i <= y2; i++)
{
sum += matrix[x2][i];
}
cout << sum << "\n";
}
}
Tester's Solution
#include <iostream>
#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <random>
#ifdef HOME
#include <windows.h>
#endif
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T &a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x = 0;
int cnt = 0;
int fi = -1;
bool is_neg = false;
while (true) {
char g = getchar();
if (g == '-') {
assert(fi == -1);
is_neg = true;
continue;
}
if ('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if (cnt == 0) {
fi = g - '0';
}
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if (g == endd) {
assert(cnt > 0);
if (is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
}
else {
//assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert(g != -1);
if (g == endd) {
break;
}
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l, r, ' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l, r, '\n');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
int main(int argc, char** argv)
{
#ifdef HOME
if(IsDebuggerPresent())
{
freopen("../in.txt", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
const int maxV = 1002;
vector<vector<int>> v(maxV, vector<int>(maxV));
forn(i, maxV)
{
v[i][0] = i ? v[i - 1][0] + i : 1;
fore(j, 1, maxV-1)
{
v[i][j] = v[i][j - 1] + i + j + 1;
}
}
vector<vector<int>> dp(1000, vector<int>(1000));
int T = readIntLn(1, 1000);
forn(tc, T)
{
int x1 = readIntSp(1, 1000);
int y1 = readIntSp(1, 1000);
int x2 = readIntSp(x1, 1000);
int y2 = readIntLn(y1, 1000);
--y1, --x1, --y2, --x2;
dp[y1][x1] = v[y1][x1];
fore(i, y1, y2)
{
fore(j, x1, x2)
{
if (i != y1)
{
dp[i][j] = dp[i - 1][j] + v[i][j];
if (j != x1)
dp[i][j] = max(dp[i][j - 1] + v[i][j], dp[i][j]);
}
else if(j != x1)
dp[i][j] = dp[i][j-1] + v[i][j];
}
}
printf("%d\n", dp[y2][x2]);
}
assert(getchar() == -1);
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class TLAPM{
//SOLUTION BEGIN
int max = 2000;
int[][] mat, row = new int[1+max][1+max], col = new int[1+max][1+max];
void pre() throws Exception{
mat = new int[1+max][1+max];
for(int d = 2, val = 1; d <= 2*max; d++){
for(int r = 1; r < d; r++, val++){
int c = d-r;
if(Math.min(r, c) >= 1 && Math.max(r, c) <= max){
mat[r][c] = val;
row[r][c] = row[r][c-1]+mat[r][c];
col[r][c] = col[r-1][c]+mat[r][c];
}
}
}
}
void solve(int TC) throws Exception{
int x1 = ni(), y1 = ni(), x2 = ni(), y2 = ni();
int ans = col[x2][y1]-col[x1-1][y1]+row[x2][y2]-row[x2][y1];
pn(ans);
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new TLAPM().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()