PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter:
Tester: Istvan Nagy
Editorialist: Taranpreet Singh
DIFFICULTY
Easy-Medium
PREREQUISITES
Coordinate compression and difference arrays
PROBLEM
Given two lists of segments A and B containing N and M segments respectively. A segment is represented by endpoints [L, R] and its length is given by R-L.
Compute the sum of length of intersection of every pair of segments a and b where a \in A and b \in B
QUICK EXPLANATION
- If some interval [L, R] is covered by x segments in A and y segments in B, then it contributes (R-L)*x*y to the required total.
- Divide the whole number line into disjoint segments and count the number of segments in A and B containing those segments.
- If we divide the number line based on start and end points of all segments, we automatically get disjoint segments.
- In order to compute the number of segments in given lists covering some interval, we can use difference arrays.
EXPLANATION
Slow solution
The naive solution would be to consider each pair of segments and add the length of its intersection, which works in O(N*M), which would time out.
Going even slower
If we split the whole number line into intervals of size one, then we can try each interval one by one and count the number of segments in A and B which contain current interval.
Let’s say we are considering interval [p, p+1], there are x segments in A which contain this interval and y segments in B which contain this interval. Then we can see that this interval contributes to the final sum x*y times.
Why: Suppose we iterate over all pair of segments. For interval (p, p+1) and pair of segments (l_1, r_1) \in A and (l_2, r_2) \in B, this interval is included in intersection of (l_1, r_1) and (l_2, r_2) only when both of these contain interval (p, p+1). Since there are x candidates for (l_1, r_1) in A and y candidates for (l_2, r_2) in B, hence this interval (p, p+1) is counted x*y times.
So this way, we have found a very slow solution, considering each interval on number line one by one, and then iterating over each pair.
Observation 1
Considering one segment in A, we can see that it covers a continuous range of intervals we divided the whole number line into.
So if we have an array cntA where cntA_i denote the number of segments in A which contain i-th interval of number line, and similarly cntB for list of segments in B, then we can rewrite the required sum as
\displaystyle \sum_{i = 1}^{MX} cntA_i * cntB_i where MX denote the number of intervals. So if we can somehow compute cntA and cntB arrays quickly, then we can compute required sum in O(MX) time.
Observation: We can see that a segment contain some continuous intervals of number line.
That means, a single segment [L, R] in A increase cntA_i, cntA_{i+1}, cntA_{i+1}, \ldots cntA_{j} for some i \leq j by one.
So we need to perform range additions on both cntA and cntB and determine the final values. The data structure difference array supports the very same updates.
Hence, using two difference arrays, we can compute cntA and cntB in O(N+M) time, and then compute the sum of intersections in O(MX) time, leading to O(N+M+MX) time.
Since currently all segments have 1 \leq L < R \leq 10^8, MX ~ 10^8, hence this solution needs to be optimized too.
Observation 2
Till now, we split the whole number line into intervals of length 1. But we don’t need to. If we can reduce the number of intervals, we can reduce the time complexity of our previous solution.
Observation: We only need to split number line at positions where some interval begin, or ends in any segment in any list.
Why: Let’s assume we have made intervals of size one. Now start merging adjacent intervals which have both cntA_i and cntB_i same. Keep doing till we can. Now all adjacent intervals shall have atleast cntA_i different or cntB_i different. But this can happen only at positions which are start or end point of some segments in set A or B.
Hence, by splitting the number line into intervals only at positions where some segment begin or ends, we can reduce the number of intervals.
Following image depicts how the number line is divided into intervals.
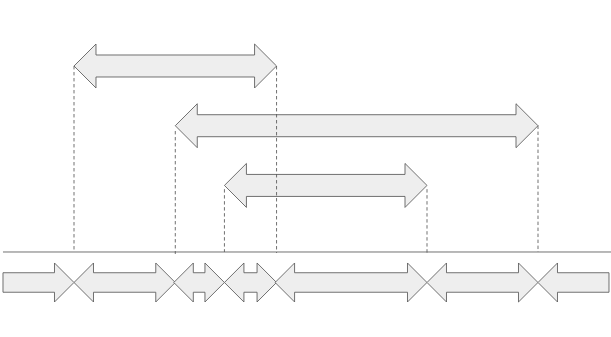
The number of intervals is guaranteed to be of the order of N+M, hence the whole time complexity comes down to O((N+M)*log(N+M)) which shall fit within time limit.
We also need to account for the length of intervals, since each interval may have different length. It can be handled by adding all start and end positions into a sorted list and considering intervals one by one.
Following implementations can be referred in case of doubts.
TIME COMPLEXITY
The time complexity is O((N+M)*log(N+M)) per test case.
The memory complexity is O(N+M) per test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
struct point{
public:
int loc, id, val;
point(int a, int b, int c){
loc = a; id = b; val = c;
}
};
const int maxt = 1e5;
const int maxn = 1e5;
const int maxm = 1e5;
const int maxtn = 2e5;
const int maxtm = 2e5;
const int maxv = 1e8;
int main()
{
int t; cin >> t;
while(t-- > 0){
int n, m; cin >> n >> m;
vector<point> v;
for(int i = 0; i < n + m; i++){
int l, r; cin >> l >> r;
int id = i < n ? 0 : 1;
v.push_back(point(l, id, 1)); v.push_back(point(r, id, -1));
}
sort(v.begin(), v.end(), [](const point& A, const point& B) {
return A.loc < B.loc;
});
long long int ans = 0; long long int c[] = {0, 0}, prv = -1;
for(int i = 0; i < 2 * (n + m);){
if(prv != -1){
ans += c[0] * c[1] * (v[i].loc - prv);
}
int j = i;
while(j < 2 * (n + m) && v[j].loc == v[i].loc){
point p = v[j];
c[p.id] += p.val;
++j;
}
prv = v[i].loc;
i = j;
}
cout << ans << endl;
}
}
Tester's Solution
#include <iostream>
#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <random>
#ifdef HOME
#include <windows.h>
#endif
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T& a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T& a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x = 0;
int cnt = 0;
int fi = -1;
bool is_neg = false;
while (true) {
char g = getchar();
if (g == '-') {
assert(fi == -1);
is_neg = true;
continue;
}
if ('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if (cnt == 0) {
fi = g - '0';
}
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if (g == endd) {
assert(cnt > 0);
if (is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
}
else {
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert(g != -1);
if (g == endd) {
break;
}
// if(g == '\r')
// continue;
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l, r, ' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l, r, '\n');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
int main(int argc, char** argv)
{
#ifdef HOME
if(IsDebuggerPresent())
{
freopen("../TOVERLP_1.in", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
int T = readIntLn(1, 100'000);
int sumN = 0;
int sumM = 0;
forn(tc, T)
{
int N = readIntSp(1, 100'000);
int M = readIntLn(1, 100'000);
sumN += N;
sumM += M;
vector<int> AS(N), AE(N);
vector<int> BS(M), BE(M);
forn(i, N)
{
AS[i] = readIntSp(1, 100'000'000);
AE[i] = readIntLn(AS[i] + 1, 100'000'000);
}
forn(i, M)
{
BS[i] = readIntSp(1, 100'000'000);
BE[i] = readIntLn(BS[i] + 1, 100'000'000);
}
sort(AS.begin(), AS.end());
sort(AE.begin(), AE.end());
sort(BS.begin(), BS.end());
sort(BE.begin(), BE.end());
int ASIndex = 0, AEIndex = 0;
int BSIndex = 0, BEIndex = 0;
int actPos = 0;
uint64_t res = 0;
while (AEIndex < AE.size() && BEIndex < BE.size())
{
int nextPos = 1e9;
if (ASIndex < AS.size())
{
nextPos = min(nextPos, AS[ASIndex]);
}
nextPos = min(nextPos, AE[AEIndex]);
if (BSIndex < BS.size())
{
nextPos = min(nextPos, BS[BSIndex]);
}
nextPos = min(nextPos, BE[BEIndex]);
uint64_t AD = ASIndex - AEIndex;
uint64_t BD = BSIndex - BEIndex;
res += (nextPos - actPos) * AD * BD;
actPos = nextPos;
while (ASIndex < AS.size() && AS[ASIndex]<= actPos)
{
++ASIndex;
}
while (AEIndex < AE.size() && AE[AEIndex] <= actPos)
{
++AEIndex;
}
while (BSIndex < BS.size() && BS[BSIndex] <= actPos)
{
++BSIndex;
}
while (BEIndex < BE.size() && BE[BEIndex] <= actPos)
{
++BEIndex;
}
}
printf("%llu\n", res);
}
assert(sumN <= 200'000);
assert(sumM <= 200'000);
assert(getchar() == -1);
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class TOVERLP{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), M = ni();
int[][] A = new int[N][2], B = new int[M][2];
TreeSet<Integer> events = new TreeSet<>();
for(int i = 0; i< N; i++){
A[i] = new int[]{ni(), ni()};
events.add(A[i][0]);
events.add(A[i][1]);
}
for(int i = 0; i< M; i++){
B[i] = new int[]{ni(), ni()};
events.add(B[i][0]);
events.add(B[i][1]);
}
int P = events.size();
int[] points = new int[P];
int c = 0;
HashMap<Integer, Integer> map = new HashMap<>();
for(int x:events){
map.put(x, c);
points[c++] = x;
}
//seg[i] = points[i]-points[i-1], seg[0] = undefined.
int[] sumA = new int[1+P], sumB = new int[1+P];
for(int[] a:A){
sumA[map.get(a[0])+1]++;
sumA[map.get(a[1])+1]--;
}
for(int[] b:B){
sumB[map.get(b[0])+1]++;
sumB[map.get(b[1])+1]--;
}
long ans = 0;
long curA = 0, curB = 0;
for(int i = 1; i< P; i++){
curA += sumA[i];
curB += sumB[i];
ans += curA * curB * (points[i]-points[i-1]);
}
pn(ans);
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new TOVERLP().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()


