PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Video Editorial
Author: Sahil Chimnani
Tester: Suchan Park
Editorialist: Sahil Chimnani
DIFFICULTY:
CakeWalk
PREREQUISITES:
Basic programming, Array
PROBLEM:
There are N sticks placed in a straight line where i^{th} stick has height A_i. The task is to cut all the sticks completely i.e. the height of each stick becomes 0 by performing below operations. In one operation:
- Choose an integer H and fix a cutter at height H from the ground.
- The cutter moves from the 1^{st} to the N^{th} stick and cuts the upper part of all the sticks with a height greater than H.
- Suppose M(M≤N) upper parts were cut during the cutting process. You need to choose H such that all the M parts are of equal length.
If A=[5,3,5], some valid values for H are 3, 4 which will cut upper parts of 2 sticks with length [2,2] and [1,1] respectively. H = 2 is an invalid choice because this will cut upper parts of 3 sticks with length [3,1,3] i.e unequal length of upperparts. The task is to print the minimum number of operations needed to cut all the sticks completely.
The problem is to be solved for T number of test cases.
QUICK EXPLANATION:
- The minimum number of operations needed to cut all the sticks completely is the number of non- zero distinct elements in the array A.
EXPLANATION:
There are 3 simple observations leading to the solution:
Observation 1:
- Sticks with zero height (A_i = 0) can be removed from the array A as there won’t be any impact on their height in any operation.
Observation 2:
- Any number of sticks having the same height can be replaced with one stick of that height. While performing a cutting operation, the cutter moves from 1^{st} to the N^{th} stick and cuts the upper part of all the sticks with a height greater than H, and it will lead to an identical impact on the sticks with the same height.
Observation 3:
- From the above 2 observations, we have an array with non-zero and distinct values. Now in one operation, we can fix the cutter at the height of the second tallest stick. After performing the operation, the tallest stick will become equal to the height of the second tallest stick. Now, as these two sticks are having the same height can be replaced with one stick according to observation 2.
Thus, the minimum number of operations needed can be calculated as the number of non-zero distinct elements in the array A.
Thanks for reading, hope you enjoyed the editorial ![]()
SOLUTIONS:
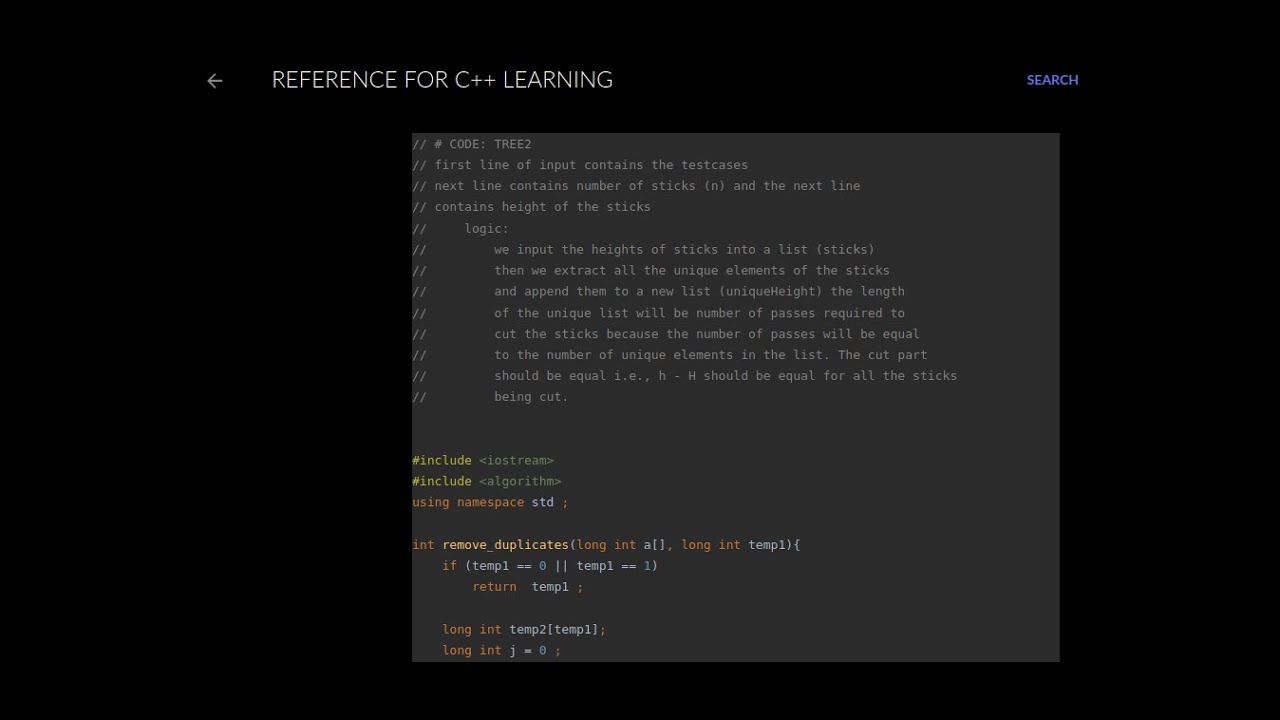
Setter's Solution(Language: CPP)
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--){
int n;
cin >> n;
set<int> s;
for(int i = 0;i < n;i++) {
int num;
cin >> num;
if(num > 0)
s.insert(num);
}
cout << s.size() << "\n";
}
return 0;
}
Tester's Solution(Language: Kotlin)
// Kotlin
class TREE2_SOLVER {
fun solve() {
val N = readLine()!!.toInt()
val A = readLine()!!.split(' ').map(String::toInt)
println(A.filter{ it > 0 }.toSet().size)
}
}
fun main(args: Array<String>) {
val T = readLine()!!.toInt()
require(T in 1..50)
repeat(T) {
TREE2_SOLVER().solve()
}
}