PROBLEM LINK:
Author: Hasin Rayhan Dewan Dhruboo
Tester: Raja Vardhan Reddy
Editorialist: William Lin
DIFFICULTY:
Medium Hard
PREREQUISITES:
Trees, Lowest Common Ancestor, Prefix sums, DFS order
PROBLEM:
Given a tree with N nodes, the beauty of the tree is \sum_{i=1}^N A_i \cdot F_i, where A_i is given and F_i is the number of distinct colors in the subtree of i. You are given Q updates of the form (a, x), which sets the color of node a to x. Find the beauty of the tree after each update.
QUICK EXPLANATION:
Whenever we color/uncolor a node u, all nodes on the path from u to one of its ancestors will have F_i increased by 1 or decreased by 1, so we update the beauty by adding or subtracting the sum of A_i on that path. To find that path, for each color, we maintain a set of the nodes with that color, sorted by dfs order.
EXPLANATION:
Let’s split each update into two operations: uncoloring a node (so that it has no color) and coloring it with a new color. Both operations are similar, so I will only focus on the second operation.
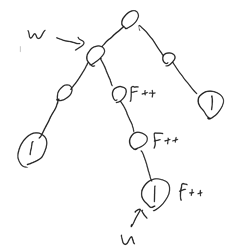
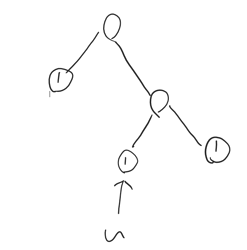
When we color a node u with a color x, some of the ancestors of u will now have color x in their subtrees, so their F_i will increase by 1. An example is shown in the picture below, where color 1 is added to u:
In this example, 3 ancestors (including u) have their F_i increased by 1. However, w (and its ancestors) do not have their F_i increased as they already contained a node with color 1 in their subtree.
Let’s suppose that we somehow know how to find w. How does the answer change? Since all nodes on the path from u to w (not including w) have their F_i increased by 1, the beauty of the tree increases by the sum of A_i for all nodes on the path from u to w. We can find the sum of A_i on the path efficiently by precalculating prefix sums of A_i from the root to each node.
What remains is to find w, the lowest ancestor of u that does not have its F_i changed.
One inefficient approach is as follows: Let’s consider all nodes with color x. For each of those nodes, we will find the lowest common ancestor of that node with u. That lowest common ancestor is the lowest node which contains both u and the node with color x in its subtree. The lowest of all such lowest common ancestors will be w (the lowest node which contains u with any node of color x in its subtree).
How do we optimize this? If we sort all nodes with color x by their dfs order, we only need to check the node which is before u in the dfs order and the node which is after u in the dfs order. This is kind of intuitive and is somewhat well-known, but unfortunately I don’t know how to prove it rigorously. Update: You can see @kshitij_789’s proof in this comment below.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
typedef vector<int> vi;
typedef vector<pair<int,int> > vpi;
const int maxn = 100009;
const int LOG = 19;
vector < int > edges[maxn];
pair < int , int > upds[maxn];
vector < int > perColorNode[maxn];
int shurutime[maxn], seshtime[maxn], Parmain[maxn], Dmain[maxn], Color[maxn], perNodeVal[maxn];
long long nodetorootsum[maxn];
int tmme;
long long curAns = 0;
map < int , int > initial_map[maxn];
pair < int , int > allupdates[maxn];
void Merge(int pos1, int pos2)
{
if(initial_map[pos1].size() < initial_map[pos2].size()) {
initial_map[pos1].swap(initial_map[pos2]);
}
for(auto e : initial_map[pos2]) initial_map[pos1][e.first] = 1;
}
void dfs1(int pos, int par, int lvl, long long val)
{
shurutime[pos] = ++tmme;
Parmain[pos] = par;
Dmain[pos] = lvl;
nodetorootsum[pos] = val;
initial_map[pos][Color[pos]] = 1;
// cout << pos << endl;
for(int to : edges[pos]){
if(to == par) continue;
dfs1(to, pos, lvl + 1, val + (long long) perNodeVal[to]);
Merge(pos, to);
}
curAns += (long long)perNodeVal[pos] * (long long)initial_map[pos].size();
seshtime[pos] = tmme;
}
struct sparseTable{
int color;
vector < vector < int > > P, edges;
vector < int > Par, D, intime, outtime;
map < int , int > mapping, rev;
int ttme;
int n;
vector < int > tree;
void Clear(){
color = n = ttme = 0;
tree.clear(); P.clear(); edges.clear();
Par.clear(), D.clear(), intime.clear(), outtime.clear();
mapping.clear(), rev.clear();
}
///point update, range query
///initial elements at tree[n]....tree[2*n-1]
void build(int _n){
n = _n;
tree.resize(2 * n + 10, 0);
}
void update(int p,int value){
for(tree[p+=n]=value; p>1; p>>=1)
tree[p>>1]=(tree[p] + tree[p^1]);
}
//outputs max(l,r-1)
int query(int l,int r){
int res=0;
for(l+=n, r+=n; l<r; l>>=1, r>>=1) {
if(l&1) res=(res + tree[l++]);
if(r&1) res=(res + tree[--r]);
}
return res;
}
void sparseMain(int n)
{
for(int i=1; i<=n; i++) for(int j=0; j<LOG; j++) P[i][j] = 0;
for(int i=1; i<=n; i++) P[i][0] = Par[i];
for(int j=1; j<LOG; j++){
for(int i=1; i<=n; i++){
if(P[i][j-1] != 0){
int x = P[i][j-1];
P[i][j] = P[x][j-1];
}
}
}
}
void buildSparse(int n){
P.resize(n + 1), Par.resize(n + 1, 0), D.resize(n + 1, 0), mapping.clear(), rev.clear();
intime.resize(n + 1, 0), outtime.resize(n + 1, 0);
for(int i = 1; i <= n; i++) P[i].resize(LOG), Par[i] = Parmain[i], D[i] = Dmain[i], mapping[i] = rev[i] = i, intime[i] = shurutime[i], outtime[i] = seshtime[i];
sparseMain(n);
}
void dfs(int pos, int par, int lvl)
{
D[pos] = lvl, Par[pos] = par, intime[pos] = ++ttme;
for(int to : edges[pos]) dfs(to, pos, lvl + 1);
outtime[pos] = ttme;
}
void buildSparse(vpi &alledges, vector < int > &subset){
int cur = 0;
mapping.clear(), rev.clear();
for(auto val : subset) mapping[val] = ++cur, rev[cur] = val;
for(auto &e : alledges) {
if(mapping[e.first] == 0) assert(0);
if(mapping[e.second] == 0) assert(0);
e.first = mapping[e.first];
e.second = mapping[e.second];
}
edges.resize(cur + 1), P.resize(cur + 1), Par.resize(cur + 1, 0), D.resize(cur + 1, 0);
intime.resize(cur + 1, 0), outtime.resize(cur + 1, 0), ttme = 0;
for(int i = 1; i <= cur; i++) P[i].resize(LOG);
for(auto e : alledges){
if(e.first > cur || e.second > cur) assert(0);
edges[e.first].push_back(e.second);
}
dfs(1, 0, 1);
sparseMain(cur);
build(cur);
for(int i = 1; i <= cur; i++) if(Color[rev[i]] == color) update(i - 1, 1);
}
int LCA(int p,int q){
p = mapping[p];q = mapping[q];
if(p == 0 || q == 0) assert(0);
if(D[p]<D[q]) swap(p,q);
int Log = log2(D[p])+1;
for(int i=Log;i>=0;i--) if(D[p]-D[q] >= (1<<i)) p = P[p][i];
if(p==q) return p;
for(int i=Log;i>=0;i--) if(P[p][i]!=0 && P[p][i] != P[q][i]) {p = P[p][i]; q = P[q][i];}
int LCA = Par[p];
return LCA;
}
int FindClosestNonzeroParent(int pos)
{
for(int i = LOG - 1; i >= 0; i--){
if(P[pos][i] == 0) continue;
int tmp = P[pos][i];
int beg = intime[tmp], ed = outtime[tmp];
if(query(beg - 1, ed) == 0) pos = tmp;
}
return Par[pos];
}
void Set(int pos, int setBit){
int curpos = pos;
pos = mapping[pos];
if(pos == 0) assert(0);
if(setBit != 1 && setBit != -1) assert(0);
if(setBit == -1) update(intime[pos] - 1, 0);
// cout << "yo : " << curpos << ' ' << color << ' ' << query(intime[pos] - 1, outtime[pos]) << endl;
///if the subtree-sum of pos is already non-zero, that means changing it won't affect any nodes distinct color count
if(query(intime[pos] - 1, outtime[pos]) == 0){
int closestPar = FindClosestNonzeroParent(pos);
closestPar = rev[closestPar];/// even if pos = 0, rev[pos] should be 0, so it's okay
curAns += (nodetorootsum[curpos] - nodetorootsum[closestPar]) * setBit;
// cout << curpos << ' ' << setBit << ' ' << closestPar << ' ' << nodetorootsum[curpos] << ' ' << nodetorootsum[closestPar] << endl;
}
if(setBit == 1) update(intime[pos] - 1, 1);
return;
}
} trees[maxn];
void compressTree(vector<int>& li, vpi& ret) {
auto cmp = [&](int a, int b) {
return shurutime[a] < shurutime[b];
};
sort(li.begin(),li.end(), cmp);
int m = li.size()-1;
for(int i=0; i<m; i++) {
int a = li[i], b = li[i+1];
li.push_back(trees[0].LCA(a, b));
}
sort(li.begin(),li.end(), cmp);
li.erase(unique(li.begin(),li.end()), li.end());
ret.clear();
for(int i=0; i<li.size()-1; i++) {
int a = li[i], b = li[i+1];
ret.emplace_back(trees[0].LCA(a, b),b);
}
}
int main()
{
// freopen("in01.txt", "r", stdin);
//freopen("outj01.txt", "w", stdout);
int t, cs = 1;
cin >> t;
while(t--){
int n, q;
scanf("%d %d", &n, &q);
tmme = curAns = 0;
for(int i = 1; i <= n; i++){
edges[i].clear();
perColorNode[i].clear(); initial_map[i].clear();
trees[i].Clear();
}
for(int i = 1; i < n; i++){
int x, y;
scanf("%d %d", &x, &y);
edges[x].push_back(y);
edges[y].push_back(x);
}
for(int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
Color[i] = x;
perColorNode[x].push_back(i);
}
for(int i = 1; i <= n; i++) scanf("%d", &perNodeVal[i]);
for(int i = 1; i <= q; i++){
int x, y;
scanf("%d %d", &x, &y);
upds[i] = {x, y};
perColorNode[y].push_back(x);
allupdates[i] = {x, y};
}
dfs1(1, 0, 1, perNodeVal[1]);
trees[0].buildSparse(n);
int totsize = 1;
for(int i = 1; i <= n; i++){
if(perColorNode[i].size() == 0) continue;
vpi tmpEdge;
compressTree(perColorNode[i], tmpEdge);
// cout << "for i : " << i << endl;
// for(auto e : tmpEdge) cout << e.first << ' ' << e.second << endl;
// cout << endl << endl;
if(tmpEdge.size() + 1 != perColorNode[i].size()) assert(0);
trees[i].color = i;
trees[i].buildSparse(tmpEdge, perColorNode[i]);
totsize += trees[i].mapping.size();
// cout << "done" << endl;
}
if(totsize > 2 * (n + q)) assert(0);
for(int i = 1; i <= q; i++){
int pos = allupdates[i].first;
int nxtClr = allupdates[i].second;
int prvColor = Color[pos];
// cout << "after : " << i << ' ' << pos << ' ' << prvColor << ' ' << nxtClr << endl;
trees[prvColor].Set(pos, -1);
trees[nxtClr].Set(pos, 1);
Color[pos] = nxtClr;
printf("%lld\n", curAns);
// cout << endl;
}
}
return 0;
};
Tester's Solution
//raja1999
//#pragma comment(linker, "/stack:200000000")
//#pragma GCC optimize("Ofast")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,avx,avx2")
#include <bits/stdc++.h>
#include <vector>
#include <set>
#include <map>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <climits>
#include <utility>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
//setbase - cout << setbase (16)a; cout << 100 << endl; Prints 64
//setfill - cout << setfill ('x') << setw (5); cout << 77 <<endl;prints xxx77
//setprecision - cout << setprecision (14) << f << endl; Prints x.xxxx
//cout.precision(x) cout<<fixed<<val; // prints x digits after decimal in val
using namespace std;
using namespace __gnu_pbds;
#define f(i,a,b) for(i=a;i<b;i++)
#define rep(i,n) f(i,0,n)
#define fd(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
#define mp make_pair
#define vi vector< int >
#define vl vector< ll >
#define ss second
#define ff first
#define ll long long
#define pii pair< int,int >
#define pll pair< ll,ll >
#define sz(a) a.size()
#define inf (1000*1000*1000+5)
#define all(a) a.begin(),a.end()
#define tri pair<int,pii>
#define vii vector<pii>
#define vll vector<pll>
#define viii vector<tri>
#define mod (1000*1000*1000+7)
#define pqueue priority_queue< int >
#define pdqueue priority_queue< int,vi ,greater< int > >
//#define int ll
typedef tree<
int,
null_type,
less<int>,
rb_tree_tag,
tree_order_statistics_node_update>
ordered_set;
//std::ios::sync_with_stdio(false);
int tim=0;
int a[100005],in[100005],out[100005],par[100005][25],arr[100005],st[500005];
ll sum[100005],res[100005];
int n;
vector<vi>adj(100005);
vector<vi>pos(100005);
vector<viii>op(100005);
vi col;
ll ans[100005];
int c[100005],q;
set<int>act;
set<int>::iterator it;
int dfs(int u,int p,ll s){
int i;
sum[u]=a[u]+s;
par[u][0]=p;
in[u]=tim;
arr[tim]=u;
tim++;
rep(i,adj[u].size()){
if(adj[u][i]!=p)
dfs(adj[u][i],u,sum[u]);
}
out[u]=tim;
}
int build(int s,int e,int node){
if(s==e){
st[node]=0;
return 0;
}
int mid=(s+e)/2;
build(s,mid,2*node);
build(mid+1,e,2*node+1);
st[node]=st[2*node]+st[2*node+1];
return 0;
}
int update(int s,int e,int node,int pos,int val){
if(s>pos||e<pos){
return 0;
}
if(s==e){
st[node]=val;
return 0;
}
int mid=(s+e)/2;
update(s,mid,2*node,pos,val);
update(mid+1,e,2*node+1,pos,val);
st[node]=st[2*node]+st[2*node+1];
return 0;
}
int query(int s,int e,int node,int l,int r){
if(s>r||e<l){
return 0;
}
if(l<=s&&r>=e){
return st[node];
}
int mid=(s+e)/2;
return query(s,mid,2*node,l,r)+query(mid+1,e,2*node+1,l,r);
}
ll add(int u){
if(query(0,n-1,1,in[u],out[u]-1)>=1){
update(0,n-1,1,in[u],1);
return 0;
}
int u1=u,i;
fd(i,20,0){
if(par[u][i]!=-1){
if(query(0,n-1,1,in[par[u][i]],out[par[u][i]]-1)==0){
u=par[u][i];
}
}
}
update(0,n-1,1,in[u1],1);
ll val=0;
if(u==0){
val+=sum[u1];
}
else{
val+=sum[u1]-sum[par[u][0]];
}
return val;
}
ll remove(int u){
update(0,n-1,1,in[u],0);
if(query(0,n-1,1,in[u],out[u]-1)>=1){
return 0;
}
int u1=u,i;
fd(i,20,0){
if(par[u][i]!=-1){
if(query(0,n-1,1,in[par[u][i]],out[par[u][i]]-1)==0){
u=par[u][i];
}
}
}
ll val=0;
if(u==0){
val-=sum[u1];
}
else{
val-=sum[u1]-sum[par[u][0]];
}
return val;
}
int reset(){
int i;
build(0,n-1,1);
rep(i,n){
adj[i].clear();
}
rep(i,col.size()){
op[col[i]].clear();
pos[col[i]].clear();
}
col.clear();
rep(i,q+2){
ans[i]=0;
}
act.clear();
tim=0;
}
main(){
//std::ios::sync_with_stdio(false); cin.tie(NULL);
int t;
//cin>>t;
//t=1;
scanf("%d",&t);
while(t--){
int i,u,v,j,x,id;
ll val;
//cin>>n>>q;
scanf("%d %d",&n,&q);
reset();
rep(i,n-1){
//cin>>u>>v;
scanf("%d %d",&u,&v);
u--;
v--;
adj[u].pb(v);
adj[v].pb(u);
}
rep(i,n){
//cin>>c[i];
scanf("%d",&c[i]);
op[c[i]].pb(mp(i,mp(0,1)));
col.pb(c[i]);
}
rep(i,n){
//cin>>a[i];
scanf("%d",&a[i]);
}
dfs(0,-1,0);
f(i,1,21){
rep(j,n){
if(par[j][i-1]==-1){
par[j][i]=-1;
}
else{
par[j][i]=par[par[j][i-1]][i-1];
}
}
}
rep(i,q){
//cin>>x>>v;
scanf("%d %d",&x,&v);
x--;
if(c[x]==v){
continue;
}
pos[c[x]].pb(i+1);
op[c[x]].pb(mp(x,mp(i+1,-1)));
op[v].pb(mp(x,mp(i+1,1)));
c[x]=v;
col.pb(v);
pos[v].pb(i+1);
}
sort(all(col));
col.resize(unique(col.begin(),col.end())-col.begin());
int pre;
rep(i,col.size()){
for(it=act.begin();it!=act.end();it++){
update(0,n-1,1,in[*it],0);
}
act.clear();
val=0;
rep(j,op[col[i]].size()){
if(op[col[i]][j].ss.ff!=0){
id=j;
break;
}
act.insert(op[col[i]][j].ff);
val=add(op[col[i]][j].ff);
ans[0]+=val;
}
f(j,id,op[col[i]].size()){
if(op[col[i]][j].ss.ss==-1){
val=remove(op[col[i]][j].ff);
act.erase(op[col[i]][j].ff);
ans[op[col[i]][j].ss.ff]+=val;
}
else{
val=add(op[col[i]][j].ff);
act.insert(op[col[i]][j].ff);
ans[op[col[i]][j].ss.ff]+=val;
}
}
}
res[0]=ans[0];
rep(i,q){
res[i+1]=res[i]+ans[i+1];
//cout<<res[i+1]<<"\n";
printf("%lld\n",res[i+1]);
}
}
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ar array
const int mxN=1e5;
int n, q, c[mxN], dt, ds[mxN], d[mxN], anc[mxN][17];
vector<int> adj[mxN];
ll a[mxN], ans;
set<ar<int, 2>> s[mxN];
void dfs(int u=0, int p=-1) {
ds[u]=dt++;
anc[u][0]=p;
for(int i=1; i<17; ++i)
anc[u][i]=~anc[u][i-1]?anc[anc[u][i-1]][i-1]:-1;
for(int v : adj[u]) {
if(v==p)
continue;
a[v]+=a[u];
d[v]=d[u]+1;
dfs(v, u);
}
}
int lca(int u, int v) {
if(d[u]<d[v])
swap(u, v);
for(int i=16; ~i; --i)
if(d[u]-(1<<i)>=d[v])
u=anc[u][i];
if(u==v)
return u;
for(int i=16; ~i; --i) {
if(anc[u][i]^anc[v][i]) {
u=anc[u][i];
v=anc[v][i];
}
}
return anc[u][0];
}
void upd(int i, int x) {
//find min ancestor which already has c[i]
int w=-1;
//before i
auto it=s[c[i]].lower_bound({ds[i]});
if(it!=s[c[i]].begin()) {
--it;
w=lca(i, (*it)[1]);
++it;
}
//after i
if(it!=s[c[i]].end()) {
int w2=lca(i, (*it)[1]);
if(w<0||d[w2]>d[w])
w=w2;
}
//update ans for path
ans+=x*(a[i]-(~w?a[w]:0));
}
void solve() {
//input
cin >> n >> q;
for(int i=0; i<n; ++i)
adj[i].clear();
for(int i=1, u, v; i<n; ++i) {
cin >> u >> v, --u, --v;
adj[u].push_back(v);
adj[v].push_back(u);
}
for(int i=0; i<n; ++i)
cin >> c[i], --c[i];
for(int i=0; i<n; ++i)
cin >> a[i];
//dfs for info
dfs();
//prepare for queries
ans=0;
for(int i=0; i<n; ++i)
s[i].clear();
//add initial colors
for(int i=0; i<n; ++i) {
upd(i, 1);
s[c[i]].insert({ds[i], i});
}
//answer queries
for(int u, x; q--; ) {
cin >> u >> x, --u, --x;
//remove color of u
s[c[u]].erase({ds[u], u});
upd(u, -1);
c[u]=x;
//add new color of u
upd(u, 1);
s[x].insert({ds[u], u});
//output
cout << ans << "\n";
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()