PROBLEM LINKS:
Practice Contest
Editorialist: hackxsaras
DIFFICULTY:
Sorting, STL, Dynamic Programming
PROBLEM (in short):
There are N citizens participating in an event. The event has 3 tracks (say A,B,C in order). Each participant has to do all the three tracks in the same order. More than one participants can do B and C simultaneously whereas A has to be done separately. We can alter the order in which participants appear in the event ( order of tracks remaining same ).
Given, the time required by each of the participants for each track. Calculate the minimum time in which the whole event could be completed.
For example, suppose N = 3, and the time they need for the three tracks are as follows:
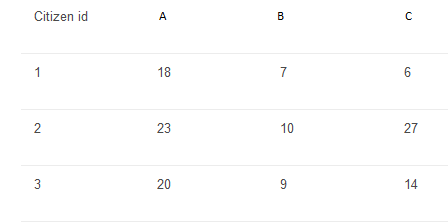
If the citizens start at time 0 and proceed in the order 1,2,3, then citizen 1 will finish at time 18+7+6 = 31, citizen 2 will finish at time 18 + (23+10+27) = 78, and citizen 3 will finish at time 18+23 + (20+9+14) = 84. The event ends at time max(31,78,84)=84. (this is not the optimal solution)
EXPLANATION:
Now with keen observation, we could establish a fact that if we arrange the citizens according to the sum of time of the tracks B and C in reverse order, the time is minimised. In the above example the order would be 2, 3,1 because (10+27) > (9+14) > (7+6) and Time to complete event = 74.
So, We have to use a comparator which will sort the citizens according to the sum of B and C in decreasing order [ O(N log N) ] and then just calculate the time required to complete the event [O(N)].
TIME COMPLEXITY:
O(N log N) (as disussed above)
SOLUTION:
If above link is dead
#include <bits/stdc++.h>
using namespace std;
#define tc int t;cin>>t;while(t--)
#define fio ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define ff(i,a,b) for(int i=a;i<b;i++)
#define fb(i,b,a) for(int i=b;i>a;i--)
#define ffi(i,a,b,c) for(int i=a;i<b;i+=c)
#define fbi(i,b,a,c) for(int i=b;i>a;i-=c)
#define clin(s) getline(cin,s)
#define MOD 1e9+7
#define pb push_back
#define mp make_pair
#define all(var) var.begin(),var.end()
bool comp(vector<int> a,vector<int> b){
return (a[2]+a[1])>(b[2]+b[1]);
}
int main() {
int n;
cin>>n;
vector<vector<int>> tri;
ff(i,0,n){
int a,b,c;
cin>>a>>b>>c;
tri.pb({a,b,c});
}
sort(all(tri),comp);
int cobol=0,spent=0;
for(int i=0;i<n;i++){
cobol+=tri[i][0];
spent=max(spent,cobol+tri[i][1]+tri[i][2]);
}
cout<<spent<<"\n";
return 0;
}
Thank You for Reading ![]()