Problem Link:
Difficulty:
Medium
Pre-requisites:
line-sweep, rank-query DS
Problem:
Given N points (Xi, Yi), and Q queries (x, y, d), find for each query how many of the N points lie within or on the boundary of the triangle formed by the triangle A(x+d, y), B(x,y), C(x,y+d).
Explanation:
This problem is solved by offline processing of the queries and using a line-sweep. Unlike most line-sweep problems, where you would sweep a (vertical) line across the X-axis (or a horizontal line across the Y-axis), and keep an active set etc, in this problem, you sweep a line of the form “x+y=c” across the plane. (Note that the slope of the hypotenuse of our query-triangle is parallel to such a sweep-line and hence the motivation for such a choice).
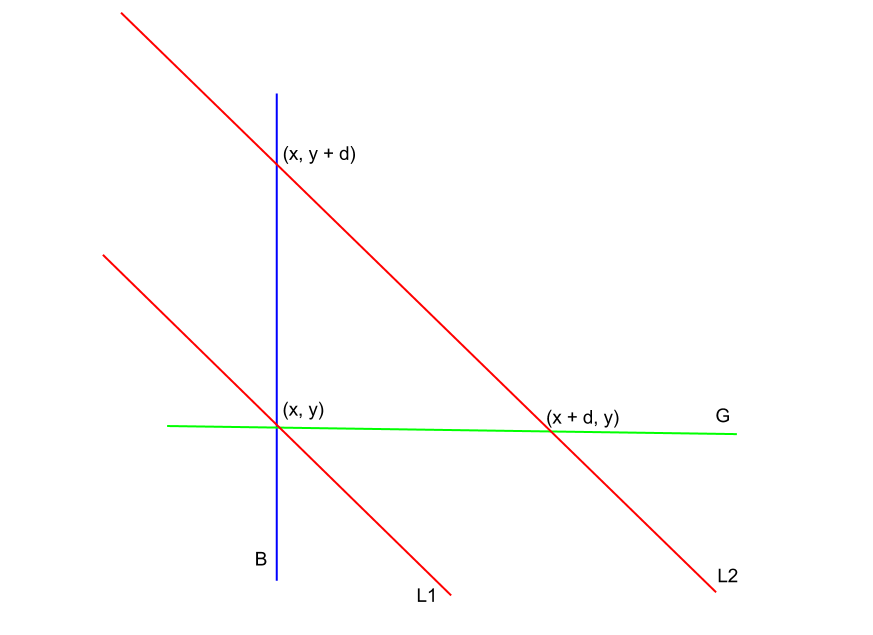
In the figure shown, we want to find the number of points in or within the boundary of L2, B and G. If we are processing lattice points in the plane in order of sweep-line, and have so far seen points below L2, we just need to remove from this set of seen points, the ones that are below G or to the left of B.
This suggests that we have an active set of “seen points”, wherein at time T, their X+Y <= T (i.e. T defines our sweep-line). From this set of seen points, we want to remove those whose X <= x, or whose Y <= y. If we store the seen points in 2 Binary Indexed Trees (BIT): one for their X coordinate, one for their Y coordinate, and query for how many points <= x, or <= y, then using principle of inclusion-exclusion, we get that the required answer = Total seen points - num(points left of B) - num(points below G) + num(points left of B and below G).
How do we find num(points left of B and below G)?
The answer lies in the line L1. When our sweep-line was at L1, we have: Total number of points seen so far = points either left of B or below G. Again by Inclusion-Exclusion, we have Total points seen so far = num(points left of B) + num(points below G) - num(points left of B and below G). From this, we can calculate num(points left of B and below G).
Thus, our algorithm is as follows:
For each of the N lattice points (X, Y), associate an event “Add (X,Y) to active set at time point X+Y”.
For every query (x, y, d), associate 2 events. Event 1 is: “Find num(points having X<=x and Y<=y) at time point x+y”.
Event 2 is: “Answer required query at time point x+y+d”.
Lets call the first kind of event as “Add point” event, the second kind of event as “L1-type” event, and the third kind as “L2-type” event.
Finally, care has to be taken to ensure that we include the boundary of our triangle formed by B, G, L2. This is done by breaking ties of time-point in the manner of L1-type event comes before any Add-point event which comes before any L2-type event.
Setter’s Solution:
Can be found here
Tester’s Solution:
Can be found here
