Practice
Div-2 Contest
Div-1 Contest
Author: Miloš Purić
Tester: Danya Smelskiy
Editorialist: Miloš Purić
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Math, Knowledge about permutation groups, Invariants
PROBLEM:
Given a permutation p of length n, find a way to sort it using at most \left \lfloor{\frac{n}{2}}\right \rfloor cyclical shifts of length 3.
QUICK EXPLANATION:
We have to find a sequence of swaps to sort the permutation. If the permutation is odd, it is not possible to sort it. Let’s process the swaps from the sequence two by two. If the current two swaps are from the same cycle, we can replace them with a single shift, otherwise we can perform two shifts. If we sort the cycles so that the ones of odd length come first, we will never use more than \left \lfloor{\frac{n}{2}}\right \rfloor operations.
EXPLANATION:
We’ll refer to our operation on indices i, j, k as shift(i,j,k) and to a regular swap on indices i, j as swap(i,j). Let’s try to decompose a shift into regular swaps of two indices.
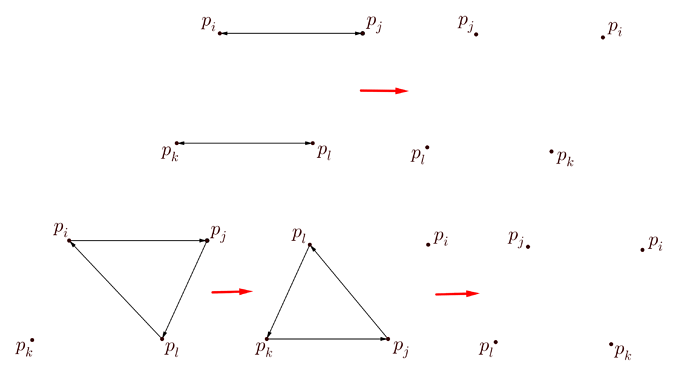
\textbf{Observation 1}: A shift(i,j,k) is equivalent to performing two swaps swap(i,j), swap(i,k) in that order (we swap the elements on those indices, rather than the indices themselves).
It can be shown that the parity of the permutation (i.e. the parity of the number of inversions) changes after a single swap has been made.
Proof 1
Let’s swap the numbers on two different indices i and j within a permutation of length n. We’ll prove that the parity of the number of inversions in this permutation changes.
The following inversions will remain after the swap: (k,i) where k<i, (i,k) where j<k, (k,j) where k<i and (j,k) where j<k.
Therefore, if we denote x as the count of numbers greater than p_i in the range (i,j) , y as the count of numbers less than p_j in the range (i,j) and a as the number of inversions before the swap had been made, the number of inversions b after the swap will be:
We add \pm1 because the pair (i,j) will either become an inversion or be one no longer. From this we infer b \not\equiv a \pmod 2, so the parity of the permutation has indeed changed.
Since a shift is equivalent to two regular swaps, we conclude that after performing a single shift the parity of the permutation does not change. Hence, if the parity of the given permutation is odd, we can never sort it using the given operation. From now on we consider only even permutations.
Let’s find all the cycles of the given permutation. For a cycle of length l (a cycle that contains l indices) we need l-1 swaps to sort it, so we characterize every cycle as a list of cycle size-1 swaps. Note that within a single cycle the first index in every swap is the same, so each cycle is represented by a list of this form:
Using \textit{Observation 1} we can replace two swaps (x,y),(x,z) with a single shift(x,y,z). If a cycle is of odd size, we need an even number of swaps to sort it, so we replace two consecutive swaps (x,y_{2i-1}),(x,y_{2i}) with a single shift(x,y_{2i-1},y_{2i}) for each 1 \leq i \leq \frac{cyclesize-1}{2} . But, if a certain cycle is of even length, then a problem arises. We have to deal with a list of an odd number of swaps, and one will be left after we process the first cyclesize-2 swaps. The following observation comes in handy when dealing with that swap.
\textbf{Observation 2}: Two regular swaps swap(i,j),swap(k,l) are equivalent to shift(i,j,l), shift(k,l,i) in the given order if i,j,k,l are pairwise distinct indices.
Here is a sketch for better understanding:
We can apply this to the swap we are left with and the first swap of the next cycle, as all the indices in them are different (they belong to different cycles). In consequence, if we are left with only one swap in a cycle, we can do it together with the first swap of the next cycle using 2 operations, and handle the next cycle without the first swap. The ‘next’ cycle will undoubtedly exist owing to the total number of swaps being even (we consider only even permutations).
However, this solution is not sufficient. There are permutations for which this solution exceeds the limit for number of operations significantly. There is an interesting proof on the upper bound of the operations it uses.
Proof 2
It can be shown that this solution uses at most \left \lfloor{\frac{2n}{3}}\right \rfloor operations.
Let f_{x,c} be the maximum number of operations this solution can use if the permutation has c cycles (we count those of length 1 too) and x=n-c (the length of the sequence of swaps, where n is the length of the permutation). Note that we consider only even x ’s because the permutation has to be even.
We can write f_{x,c} in terms of previous f ’s by considering the length of the last cycle. If the last cycle was of even length then we go to f_{x-2y,c-1} by using y operations.
If the last cycle was of odd length then we go to f_{x-2y-2,c-1} by using y+2 operations, because we have to do to the last swap of the second to last cycle with the first swap of the last cycle. In this case, we can also go to f_{x-2y-2,c-2} if we wish for the second to last cycle to have length 1. However, f_{a,b} \geq f_{a,b-1} is obviously true for all a and b \geq 1 so we can omit this.
Thus, the following recurrent relation holds true:
This expression can be rewritten in the following way (we omit the base values f_{0,c} for clarity):
The second term is obviously always bigger so:
We will now prove that f_{x,c} \leq \frac{2(x+c)}{3} for every x \geq 1 and c \geq 1 by induction on the number of cycles c.
\textbf{Base case:} f_{x,1}=\frac{x}{2} \leq \frac{2(x+1)}{3}
\textbf{Inductive step:} From the above reasoning, derived from the definition:
By the inductive hypothesis f_{a,c-1} \leq \frac{2(a+c-1)}{3} for all a \geq 1. Thus:
This shows that the statement is correct for all f's with c cycles, so the step is over.
Hence, f_{x,c} \leq \frac{2(x+c)}{3} is true for all x \geq 1 and c \geq 1.
Since n=x+c, then O \leq \frac{2n}{3} (i.e. O \leq \left \lfloor{\frac{2n}{3}}\right \rfloor) for every permutation of length n. Equality can be reached by tracing back the values of f.
To optimize it we need to consider the fact that the order of processing the cycles does not matter. We will sort all cycles so that we first process all the cycles for which we need an even number of swaps (cycles of odd size) and then all the cycles for which we need an odd number of swaps (cycles of even size). We can prove that by processing cycles in this manner we never use more than \left \lfloor{\frac{n}{2}}\right \rfloor operations.
Proof 3
Let c_e,c_o be the number of even cycles and odd cycles respectively, e_i,o_i be the size of the i-th even and i-th odd cycle respectively, l_e,l_o be the total length of all even and odd cycles (i.e. the sum of sizes of all even and odd cycles) respectively.
For processing all the cycles of odd length (each of them requires an even number of swaps) we need a operations where:
The number of cycles of even length must be even (since each of them requires an odd number of swaps). For every two adjacent cycles of even length we will do the last swap of the first cycle with the first swap of the second cycle using 2 operations. Taking that into account, for processing all the cycles of even length we need b operations where:
Summing these two up, we get that the total number of operations O is:
From this we see that O \leq \frac{n}{2} and so O \leq \left \lfloor{\frac{n}{2}}\right \rfloor. The equality can be achieved when all cycles are of even length (i.e. c_o=0).
IMPLEMENTATION NOTES:
Representing the permutation as a product of transpositions quickly (i.e. extracting all the swaps that need to be made) may be the first somewhat troubling part in case you have never done it before. It is usually being implemented in the following way:
ListOfTranspositions #an empty list of pairs - transpositions
for i = 1 . . . n:
while(a[i] != i)
#the element currently standing on position i should go to position a[i]
ListOfTranspositions.append({i,a[i]}) #add the transposition from i to a[i]
swap(a[i],a[a[i]]) #swap the corresponding values on those indices
From the fact that the parity of the permutation changes after a single swap has been made (see Proof 1), it follows that the parity of the permutation is the same as the parity of the number of transpositions in it’s representation. Consequently, we can just check if the length of the ListOfTranspositions is odd and output -1 if that is the case.
In order to be able to sort the cycles according the parity of their length, we need to create a separate list for each cycle and store each transposition in the list of the cycle it belongs to. We can achieve that by modifying the code above:
ListOfListsOfTranspositions #an empty list of lists
for i = 1 . . . n:
ListOfTranspositions #an empty list of pairs - transpositions
while(a[i] != i)
#the element currently standing on position i should go to position a[i]
ListOfTranspositions.append({i,a[i]}) #add the transposition from i to a[i]
swap(a[i],a[a[i]]) #swap the corresponding values on those indices
ListOfListsOfTranspositions.append(ListOfTranspositions)
sort(ListOfListsOfTranspositions) #sort the cycles according to their parity
Now it only remains to construct the solution by traversing the transpositions and grouping them two by two as described, in the order they are given in the ListOfListsOfTranspositions.
The time complexity of this solution is O(n \log n) and the memory complexity is O(n). The time complexity would have been O(n) if we had used counting sort for sorting the cycles.
REMARKS:
If you are not familiar with the basic terms in permutation groups, I suggest you take a look at
this article as an introduction to permutation groups with some more interesting results. Wikipedia’s articles on permutation groups and symmetric groups, which are closely related in the field of group theory, are also quite nicely written.
Problems in permutation groups and their solutions have applications in fields like bioinformatics, for example, sorting of genomic sequences. Some more applications have been pointed out in this article, which I encourage you to take a look at.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair <int,int> p;
typedef pair <p,int> t;
const int N = 2e5+23;
int a[N],b[N];
vector <vector<p>> cycles; /// all the cycles are stored here (actually the swaps that are needed to sort them)
vector <p> swaps;
vector <t> sol;
void op(int i,int j,int k){
sol.push_back(t(p(i,j),k));
}
void solve(){
cycles.clear();
swaps.clear();
sol.clear();
int n,k,parity = 0;
cin >> n >> k;
for(int i = 1; i <= n; i++){
cin >> a[i];
b[i] = a[i];
}
vector <vector<p>> oddcycles; /// we'll put all cycles of odd length here
for(int i = 1; i <= n; i++){ /// now we single out the cycles
vector <p> v;
while(a[i] != i){ /// a[i] is the position where the element currently on position i should go
v.push_back(p(i,a[i])); /// add this swap
parity++;
swap(a[i],a[a[i]]);
}
if(v.size()){
if(v.size()%2 == 0){ /// if this cycle is of even size put it into cycles
cycles.push_back(v);
}
else{ /// if it is of odd size put it here
oddcycles.push_back(v);
}
}
}
for(int i = 0; i < oddcycles.size(); i++){ /// then add all the odd length cycles to the back so that all the cycles are sorted according to their parity
cycles.push_back(oddcycles[i]);
}
if(parity%2 == 1){ /// if the permutation is odd it is impossible to sort it using given operations
cout << "-1\n";
return;
}
if(n == 3){ /// base cases, probably not needed
if(b[1] == 1){
cout << "0\n";
}
else if(b[1] == 2){
cout << "1\n";
cout << "1 2 3\n";
}
else{
cout << "1\n";
cout << "1 3 2\n";
}
return;
}
for(auto f : cycles){ /// from now on we just need the whole list of swaps, that is the vector 'swaps'
for(auto g : f){
if(g.first > g.second){
swap(g.first,g.second);
}
swaps.push_back(g);
}
}
for(int x = 0; x < swaps.size(); x += 2){ /// we process the swaps two by two
p f = swaps[x],g = swaps[x+1];
int i1 = f.first,j1 = f.second,i2 = g.first,j2 = g.second;
if(i1 > j1){
swap(i1,j1);
}
if(i2 > j2){
swap(i2,j2);
}
/// if any two indices are equal then these two swaps belong to the same cycle and we can do them using one operation
if(i1 == i2){
op(i1,j1,j2);
continue;
}
if(j1 == j2){
op(j1,i1,i2);
continue;
}
if(i1 == j2){
op(i1,j1,i2);
continue;
}
if(i2 == j1){
op(j1,i1,j2);
continue;
}
/// otherwise we have four different indices i1,j1,i2,j2 and we can do them together using two operations
op(i1,j1,j2);
op(i2,j2,i1);
}
cout << sol.size() << "\n";
for(auto f : sol){
cout << f.first.first << " " << f.first.second << " " << f.second << "\n";
}
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
/*freopen("tst.txt","r",stdin);
freopen("output.txt","w",stdout);*/
int te;
cin >> te;
while(te--){
solve();
}
}
Tester's Solution
#include <iostream>
#include <algorithm>
#include <vector>
#include <tuple>
using namespace std;
const int N = 200'005;
int n, k;
int p[N];
bool used[N];
void solve(int test_id) {
vector<pair<int, int>> two_node_cycles;
vector<tuple<int, int, int>> answer;
cin >> n >> k;
for (int i = 1; i <= n; ++i) {
cin >> p[i];
}
for (int i = 1; i <= n; ++i) {
used[i] = false;
}
for (int i = 1; i <= n; ++i) if (!used[i]) {
vector<int> cycle;
int j = i;
while (!used[j]) {
used[j] = true;
cycle.push_back(j);
j = p[j];
}
while (cycle.size() > 2) {
// x -> y -> z -> x
int z = cycle.back();
cycle.pop_back();
int y = cycle.back();
cycle.pop_back();
int x = cycle.back();
if (cycle.size() == 1)
cycle.pop_back();
answer.push_back(tie(x, y, z));
--k;
}
if (cycle.size() == 2) {
two_node_cycles.push_back(make_pair(cycle[0], cycle[1]));
}
}
while (two_node_cycles.size() > 1) {
// a -> b -> a,
// c -> d -> c
pair<int, int> fir = two_node_cycles.back();
two_node_cycles.pop_back();
pair<int, int> sec = two_node_cycles.back();
two_node_cycles.pop_back();
// b -> c -> d
// a -> b -> c
answer.push_back(tie(fir.second, sec.first, sec.second));
answer.push_back(tie(fir.first, fir.second, sec.first));
k -= 2;
}
if (!two_node_cycles.empty()) {
k = -1;
}
if (k < 0) {
cout << "-1\n";
} else {
cout << answer.size() << '\n';
for (int i = 0; i < answer.size(); ++i) {
cout << get<0>(answer[i]) << " "
<< get<1>(answer[i]) << " "
<< get<2>(answer[i]) << '\n';
}
}
return;
}
int main(int argc, const char * argv[]) {
#ifdef __APPLE__
freopen("/Users/danya.smelskiy/Documents/Danya/Resources/input.txt","r",stdin);
#endif
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int tests;
cin >> tests;
for (int i = 0; i < tests; ++i) {
solve(i);
}
return 0;
}