Problem Link:
Author: Pavel Sheftelevich
Tester: Kanstantsin Sokal
Editorialist: Sunny Aggarwal
Difficulty:
Medium
Pre-Requisite:
Geometry, Implementation, Mathematics
Problem Statement:
Given 2 triangles and a quadrilateral. We are asked to check whether it’s possible to combine these triangles by moving, flipping and/or rotating them, and cover exactly the quadrilateral with no overlap between the two triangles.
Brief Explanation:
There are no so many possible configurations in which we can combine given 2 triangles to form a quadrilateral such that there is no overlap between the triangles.
-
1 side of a triangle is put against equal length side of other triangle to form quadrilateral.
-
1 side of a triangle is put against relatively longer side of other triangle to form quadrilateral.
Check all above listed configurations.
Solution:
1^{st} Configuration
One side of the first triangle is put against the same-length side of the second triangle. This case can also degenerate into a case, when quadrangle appears to be a triangle. Any way, we should fix which sides will be put against each other and them try all possible combinations of the remaining sides to complete the quadrangle.
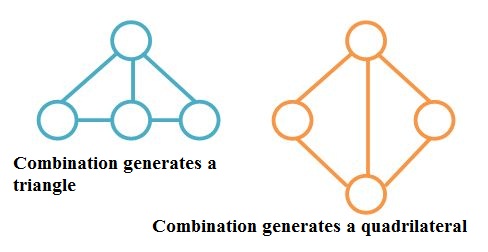
2^{nd} Configuration
One side of one triangle is put against a longer side of the other triangle in such a way, that it continues one of the sides of the second triangle (like on the picture attached to this letter). In this case, we should fix the part of the side of the second triangle, which is next to the one put against the shorter side of the first triangle, and then intersect the line formed by the part of the side and the opposite side of the quadrangle.

How to check for these configurations ?
Some Pre-Requisites
Please have a look at given code. I have tried to cover the implementation in the comments.
C++ Code
#define X first
#define Y second
#define pb push_back
#define ld long double
const ld eps = 1E-6, PI = acos(-1.0);
vector<ld>l1, l2;
pair<ld, ld>p[4];
ld dist(pair<ld, ld> A, pair<ld, ld>B) {
// finding euclidean between 2 coordinates
return sqrt( (A.X - B.X) * (A.X - B.X) + (A.Y - B.Y) * (A.Y - B.Y) );
}
ld area(pair<ld, ld>A, pair<ld, ld>B, pair<ld, ld>C) {
// finding 2 * area of triangle formed by these 3 coordinates.
return A.X * (B.Y - C.Y) + B.X * (C.Y - A.Y) + C.X * (A.Y - B.Y) ;
}
int n, m;
ld given[10][10];
ld g[10][10];
bool eq(ld a, ld b) {
return fabs(a - b) < eps;
}
ld angle(ld a, ld b, ld c) {
return acos ( (a*a + b*b - c*c) / (2.0 * a * b) );
}
ld side(ld a, ld b, ld ang) {
return sqrt( a*a + b*b - 2 * cos(ang)*a*b );
}
void assign(int a, int b, ld c) {
g[a][b] = g[b][a] = c;
}
bool check() {
if (n != m)
return false;
vector<int>perm;
for (int i = 0; i < m; i++)
perm.pb(i);
for (int i = 0; i < n; i++) {
perm.pb(perm[0]);
perm.erase(perm.begin() );
bool ok = true;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ( !eq( g[ perm[i] ][ perm[j] ], given[i][j]) ) {
ok = false;
}
}
}
if (ok) {
return true;
}
}
perm.clear();
for (int i = m - 1; i >= 0; i--)
perm.pb(i);
for (int i = 0; i < n; i++) {
perm.pb(perm[0]);
perm.erase(perm.begin() );
bool ok = true;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ( !eq( g[ perm[i] ][ perm[j] ], given[i][j]) ) {
ok = false;
}
}
}
if (ok) {
return true;
}
}
return false;
}
void solve() {
pair<ld, ld>a, b, c;
// reading first triangle
cin>>a.X>>a.Y;
cin>>b.X>>b.Y;
cin>>c.X>>c.Y;
l1.clear(); l2.clear();
l1.pb( dist(a, b) ); l1.pb ( dist(a, c) ); l1.pb( dist(b, c) );
// l1 contains length of sides of first triangle
// reading second triangle
cin>>a.X>>a.Y;
cin>>b.X>>b.Y;
cin>>c.X>>c.Y;
l2.pb( dist(a, b) ); l2.pb ( dist(a, c) ); l2.pb( dist(b, c) );
// l2 contains lengths of sides of second triangle
sort(l1.begin(), l1.end() );
sort(l2.begin(), l2.end() );
// reading quadrilateral
for (int i = 0; i < 4; i++) {
cin>>p[i].X>>p[i].Y;
}
int del = -1;
for (int i = 0; i < 4; i++) {
if ( eq( area(p[i], p[ (i + 1) % 4 ], p[ (i + 2) % 4 ]), 0.0 ) ) {
del = (i + 1) % 4;
}
}
vector<int>who;
if (del == -1) {
// quadrilateral is not of triangular form
m = 4;
for (int i = 0; i < 4; i++) {
who.pb(i);
}
}
else {
// quadrilateral is of triangular form
m = 3;
for (int i = 0; i < 4; i++) {
if (del != i) {
who.pb(i);
}
}
}
// calculate pairwise distance between the vertices of quadrilateral
for (int i = 0; i < who.size(); i++) {
for (int j = 0; j < who.size(); j++) {
given[i][j] = dist(p[who[i] ], p[who[j] ]);
}
}
// consider sides of triangles one by one in all possible order
do {
do {
// new distance matrix where we will compute distance from each vertex to each other
// vertex of configuration formed by the combination of 2 triangles considering
// their sides in the chosen order.
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
g[i][j] = 0.0;
}
}
// calculating angle using cosine rule
ld ang1 = angle(l1[0], l1[1], l1[2]);
ld ang2 = angle(l2[0], l2[1], l2[2]);
if ( eq(PI, ang1 + ang2) && eq(l1[0], l2[0]) ) {
// combination of triangle along equal sides generates a triangle as shown
// in the figure above.
n = 3;
// computing pair-wise distances
assign(0, 1, l1[2]);
assign(0, 2, l2[2]);
assign(1, 2, l1[1] + l2[1]);
}
else {
n = 4;
if (eq(l1[0], l2[0]) ) {
// combination of triangle along equal sides generates a quadrangle
// as shown in the figure above.
// computing pair-wise distances
assign(0, 1, l1[2] );
assign(1, 2, l1[1]);
assign(0, 3, l2[2]);
assign(3, 2, l2[1]);
assign(0, 2, l1[0]);
assign(1, 3, side(l1[1], l2[1], ang1 + ang2) );
}
if (eq(PI, ang1 + ang2) ) {
// combination of smaller side of triangle against longer side of
// other traingle to form a quadrangle
bool sw = false;
if (l1[0] > l2[0]) {
sw = true;
swap(l1, l2);
}
assign(0, 1, l2[0] - l1[0]);
assign(1, 2, l1[2]);
assign(2, 3, l1[1] + l2[1]);
assign(3, 0, l2[2]);
assign(1, 3, side(l1[0], l2[1], ang2) );
ld help;
help = angle(l1[0], l1[2], l1[1]);
help = PI - help;
assign(2, 0, side(l1[2], l2[0] - l1[0], help) );
if (sw) {
swap(l1, l2);
}
}
}
// check if the computed pairwise distance for this configuration of triangle is
// equal to the pair wise distances obtained from the given quadrilateral or not.
if ( check() ) {
cout<<"Yes"<<endl;
return ;
}
}
while ( next_permutation(l2.begin(), l2.end() ) );
}
while (next_permutation(l1.begin(), l1.end() ) );
cout<<"No"<<endl;
}
Time Complexity:
Implementation based
Space Complexity:
O(1)
Similiar Problems:
To be updated soon
Solution:
Setter’s solution can be found here
Tester’s solution can be found here
Feel free to post comments if anything is not clear to you.