Problem Link
Author: Stacy Hong
Tester: Misha Chorniy
Editorialist: Bhuvnesh Jain
Difficulty
MEDIUM
Prerequisites
Problem
You are given a grid with numbers written on every cell. You are required to find the largest connected component on the grid such that it contains at most 2 distinct numbers in it.
Note that editorial refers to the flowers as numbers.
Explanation
Subtask 1: N, M ≤ 100
A simple brute force which considers every pair of different numbers and performs BFS on the grid to find the connected component and their sizes is enough to pass this subtask. Below is a pseudo-code for it.
def solve(c1, c2):
res = 0
for i in [1, n]:
for j in [1, m]:
if vis[i][j] or (a[i][j] != c1 and a[i][j] != c2):
continue
# perform bfs to find size of connected component containing c1 and c2
# update res variable with maximum value
return res
ans = 0
for c1 in [1, 100]:
for c2 in [i, 100]:
# also handle case of one color only.
ans = max(ans, solve(c1, c2))
The time complexity of the above approach is O(n * m * {\text{Max(a[i][j])}}^{2}).
Subtask 2, 3: N, Q ≤ 2000
The solution approach for last 2 subtasks is same. Just difference in implementation and constant factors can lead to passing subtask 2 only.
The full solution idea relies on the brute force solution above. Instead of doing a complete BFS on the grid every time based on the type of colour you need to consider, we store the edges containing different numbers and do BFS/DSU on it. Below are the 2 different approaches for it.
Author/Tester Solution: DSU + Sorting/HashMap
First find all connected components which have the same type of numbers. Store with each component the size of the component and the index of the component as well. This can be easily done with a BFS/DFS. Now create edges between 2 component which are adjacent to each other in the grid i.e. there exists a cell in component 1 which is adjacent to a cell in component 2. Store the edges in the following format:
To avoid doing the same computation again, store only the edges such that \text{Number in component 1} < \text{Number in component 2}. This will help to reduce the constant factor by 2 in your code.
Now, we traverse each edge based on the numbers they connect and perform DSU to find the maximum connected component. Below is the explanation of sample test case in the problem.
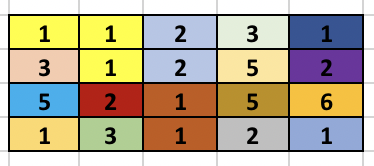
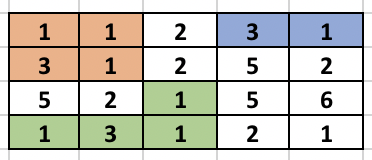
The left side image shows the different components formed after the first BFS is done. The second side image shows the result of performing DSU. So, once the BFS is done, we see that cell (2, 1) containing 3 is adjacent to cell (1, 1) containing 1, so we merge them using DSU. Again cell (4, 1) containing 1 is adjacent to cell (4, 2) containing 3 so, we merge them using DSU. The process continues as cell (4, 3) containing 1 is adjacent to (4, 2) containing 3 (which was already expanded before) and the component increases.
The only issue which needs to be taken care while implementing the above solution is resetting of DSU after every iteration. Doing it in naive manner i.e. resetting all the components to original sizes and parent as themselves will TLE even for subtask 2 as the complexity will be similar to subtask 1. Instead, we only restore the values whose parent or size changed while performing the DSU operation. This can be stored while performing the merge operation.
For more details, you can refer to the author’s or tester’s solution below.
The complexity of the above approach will be O(n * m * log(n * m)) as you will traverse each edge once. The logarithmic factor is due to sorting or using maps to store the edges. If you use hash-maps instead to store the edges, the complexity will be O(n * m) but will large constant factor.
Editorialist Solution: Edge-based Graph traversal
UPDATE: This solution is slow. The author created a counter test against it. The time complexity will be O(n^2*m^2) as pointed out in comments below. Even the test case provided is similar. Please refer to author’s solution above for full problem. Will ask Codechef team to add that case in the practice section too for help.
Instead of forming any components or performing DSU or doing BFS like the normal way, we see simple observation in the brute force approach. If, each edge connecting adjacent cells in the grid, whether having same numbers or different numbers if traversed at most twice while determining the size, the complexity will be O(8 * n * m) overall. Below is the detailed description of the idea:
First, select an edge in the grid. Find the numbers (at most 2) which will form the component. We will try to find the full component which contains this edge and make sure this component is traversed only once. For this, you start a normal BFS from each cell. You go to adjacent cell only if it is one of the 2 required numbers. While adding the node in the BFS queue, we all update the possible ways in which the edge could be traversed as part of the same component. So, cell (3, 2) containing 2 was visited from cell (2, 2) containing 1. But it could be traversed from cell (3, 3) containing 1 in future and will form the same component. So, we update all 4 directions of a cell can be visited in the same component before adding the cell in BFS queue. The BFS for a component is performed only if the edge was never traversed before in any component. The image below shows how the component is expanded in each step of BFS when the starting edge is selected as (1, 2) and (1, 3).
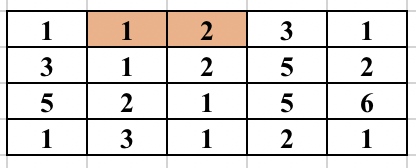
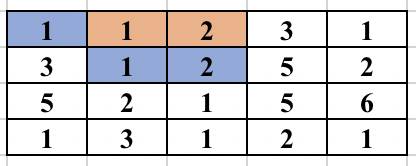
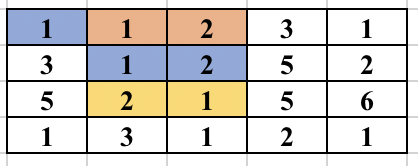
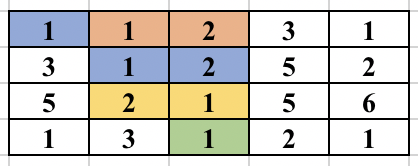
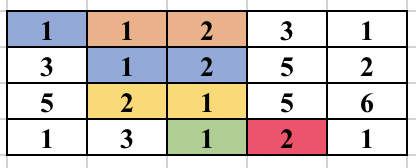
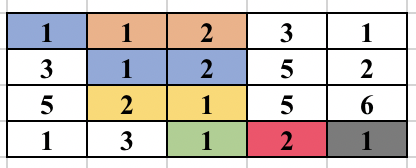
The time complexity of the above approach is O(n^2*m^2) and will pass subtask 1 only.
Once, you are clear with the above idea, you can see the editorialist implementation below for help.
Feel free to share your approach, if it was somewhat different.
Time Complexity
O(n * m)
Space Complexity
O(n * m)
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
Editorialist’s solution can be found here. (Will TLE).