Problem Link - 2 Two Paths
Problem Statement
You are given an N * M grid, A [1, 2, …, N] [1, 2, …, M], that has an integer, which may be negative, in every cell. The grid has N rows and M columns. (1,1) is the top left corner cell and (N, M) is the bottom right corner cell. You are also given an integer K.
A Path is a sequence of N cells that starts at any cell at the bottom-most row and goes up one row at a time. When you move from a row to the one above, you can only move straight-up, or up-and-left. That is, if you are at cell (i, j) you can move straight-up to the cell (i - 1, j) or up-and-left to the cell (i - 1, j - 1). You have to stay within the grid, always. Also, you are allowed to move up-and-left at most K times in a single Path.
You need to choose two Paths with the following constraints.
- The starting cells are different and have at least K other cells in between them. That is, if the starting cells are (N, a) and (N, b), then | a - b | should be greater than or equal to (K + 1).
- The Paths are non-intersecting. Two Paths are said to be intersecting if they have at least one cell in common.
The score associated with any such pair of Paths is the sum of all the values between these two Paths (including the cells on the two Paths). That is, take every cell that is on, or in between these two Paths, and add up their values.
Formally, the score for a pair of non-intersecting Paths is defined as follows. On row i, suppose one path passes through cell (i, a) and the other path passes through cell (i, b), where a < b. Then, Score[i], the score for row i, is the sum of all entries A[i][j] for a ≤ j ≤ b. The overall score is the sum of all row scores Score[i] for 1 ≤ i ≤ N.
If these were the two Paths that you had chosen, then your score would be the sum of all the values in the cells which are coloured blue:
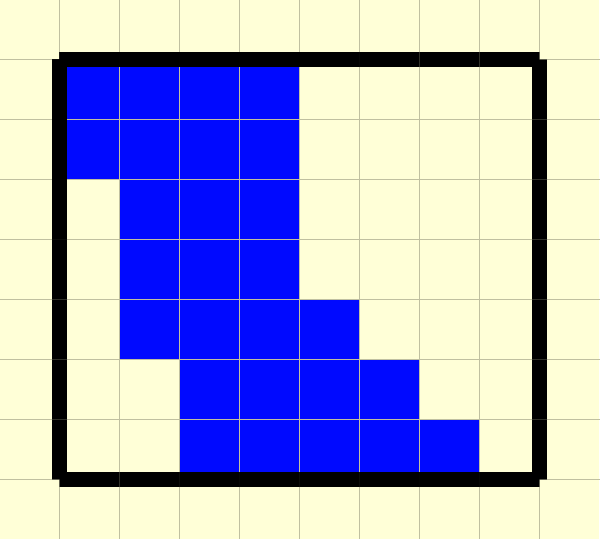
You need to choose two valid Paths such that the score is maximized, and you need to print this maximum score.
Approach
The approach involves dynamic programming to calculate the maximum scores of paths ending at each cell for a given number of leftward moves. First, for each column, compute cumulative sums from bottom to top, which helps in quickly summing up values for paths. The problem is solved in two parts: calculating the best possible score from left-to-right paths and right-to-left paths. For both parts, dynamic programming is used to track the maximum score for paths using at most K left moves. After finding the best left-to-right and right-to-left paths for each column, the solution involves checking pairs of columns that are (K + 1) apart and summing their respective scores. The final answer is the maximum of these combined scores.
Time Complexity
The time complexity is O(N \times M \times K), where N is the number of rows, M is the number of columns, and K is the maximum allowed leftward moves.
Space Complexity
The space complexity is O(N \times M) for storing the cumulative sums and dynamic programming arrays.