MOTIVATION:
I came across this problem today. Seems very interesting, yet I can’t make my mind to code this whole thing out. So, I’ll write this unofficial editorial out instead. Seems none of the problems of February Challenge 2017 have editorials. Maybe someone can write them?
Also, read this.
PROBLEM LINK:
contest
AUTHOR
mgch
DIFFICULTY
Supposedly medium, but I thought this was medium-hard (or at least \frac{\text{medium}+\text{medium-hard}}{2})
PREREQUISITES:
lca, Mo’s algorithm, persistence
PROBLEM:
Please refer link. In short: for a given (dynamic) tree, find the number of distinct elements on the path from node u to node v.
SOLUTION
(May be wrong, just something I came up with. Comments appreciated)
Before we do anything, we need a way to “find” the path from u to v. This is easy: we can use binary lifting to perform LCA queries in \mathcal{O}(\log N) time.
Tackling the static case.
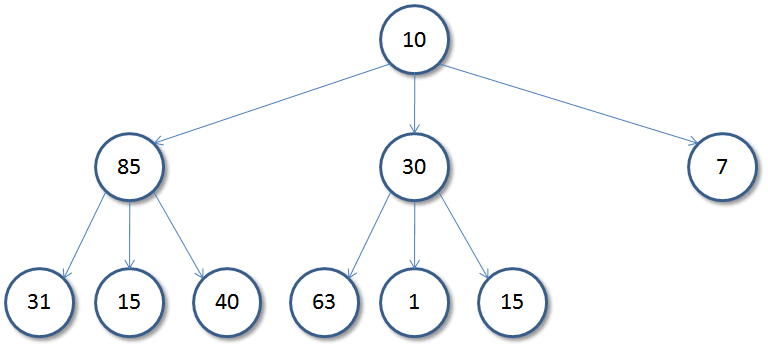
Consider taking an Euler tour around the tree. For each node, we store the in-time and the out-time, just as in the case of LCA queries. Let us denote the in-time and out-time of a node u in our dfs by \text{in}(u) and \text{out}(u). For instance, in the tree below,
The euler tour can be written as:
\text{10 85 31 31 15 15 40 40 85 30 63 63 1 1 15 15 30 7 7 10}
And \text{in}(30) = 10, \space \text{out}(30) = 17
Further, we maintain two arrays for the sake of Euler paths: one on node ID’s and one on the node values.
Assume that \text{in}(u) < \text{in}(v), then let us take two cases:
\text{Case 1.} \text{LCA}(u,v) = u. Then consider the subarray from \text{in}(u) to \text{in}(v). If we could perform the query on this range, we’d be done. Not really. What of the stray nodes that lie off to the “left” of node v which we would be including even though they arent on our path? The key is to note that these nodes occur twice in our u-v path. This is exactly the reason we stored two arrays for our Euler tour. Using the node ID array we can ascertain during Mo’s algorithm when we have a repeated (i.e. stray ) node in our range, and we can accordingly perform a \text{count[value(u)]- -} step to take care of this. Thus we can handle this accordingly using Mo’s algorithm.
\text{Case 2. LCA}(u,v) = p \neq u. In this case consider the subarray formed from \text{out}(u) to \text{in}(v). Perform the subsequent steps as in the previous case, except make one change: perform \text{count[value(p)]++} since p wasn’t taken care of in this case yet.
Dynamic case:
Making this dynamic is not that hard, but it indeed is elegant. Bring in persistence. When reading queries, for every operation \text{update u's value to } \mathcal{V} make a new node u_1 with value \mathcal{V} and attach it as a child of \text{parent}(u). Do this before the dfs/lca-binary-lifting-building. Now treat this as the static case.
Now, even though this may come as a surprise, I had never thought of implementing Mo’s algorithm on trees. Maybe that’s why it took me so long to come up with the static solution (and maybe thats why I thought it med-hard). I almost immediately made it dynamic, the persistence thing was not so hard. Though, I am really having some problem coding the static case out. In particular, whatever stuff I’m writing for for detecting stray nodes, doesn’t seem to work properly. This lead me to search online, and I found that article which mentions the same thing as my method. Can someone give some code for this part? I tried reading the AC solutions but it’s difficult to read the ultra compact code of most solutions.
TIME COMPLEXITY:
Building of the Euler tour arrays \rightarrow \mathcal{O}(N).
Building of binary lifting pointers \rightarrow \mathcal{O}(N \log N).
Queries of type 2 \rightarrow \mathcal{O}(1) per query.
Assuming Q \sim N , performing Mo on all queries of type 1 \rightarrow \mathcal{O}(N\sqrt{N}) overall.
Overall complexity assuming Q \sim N \rightarrow \mathcal{O}(N\sqrt{N}).