Hey guys, I have been trying to implement division of a number using Newton’s Method in Python. I studied about this method in an online lecture and am having trouble implementing it.
Link to the online lecture : Recitation 12: Karatsuba Multiplication, Newton's Method - YouTube
Instead of using floating point numbers I have used Python lists to represent the number.
The program takes two arguments (b and d) and is supposed to return the value of 1/b till d digits of precision. The program runs on the following formula :
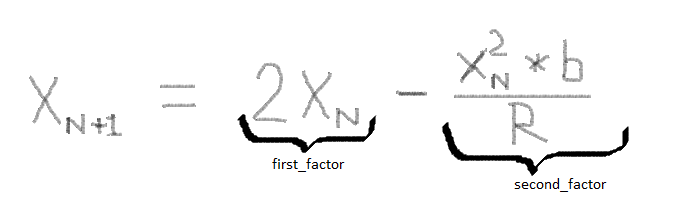
where R = 10^d
In my code I have named: Xn as prev_num , Xn+1 as next_num , 2Xn as first_factor (as shown in the photo) , (Xn^2)*b/R as second_factor (also shown in photo)
def divide(b,d):
prev_num = 1 #initial guess of 0.1
first_factor = 2*prev_num
first_factor_list = []
for i in str(first_factor):
first_factor_list.append(i)
if len(first_factor_list) < d:
first_factor_list = first_factor_list + ['0']*(d-len(first_factor_list))
if len(first_factor_list) > d:
first_factor_list = first_factor_list[:d]
second_factor = ((prev_num)**2)*b
second_factor_list = []
for i in str(second_factor):
second_factor_list.append(i)
if len(second_factor_list) > d:
second_factor_list = second_factor_list[:d]
first = int(''.join(first_factor_list))
second = int(''.join(second_factor_list))
next_num = first - second
print(next_num)
while abs(next_num - prev_num) > 1:
prev_num = next_num
first_factor = 2*prev_num
first_factor_list = []
for i in str(first_factor):
first_factor_list.append(i)
if len(first_factor_list) > d:
first_factor_list = first_factor_list[:d]
if len(first_factor_list) < d:
first_factor_list = ['0']*(d-len(first_factor_list)) + first_factor_list
second_factor = ((prev_num)**2)*b
second_factor_list = []
for i in str(second_factor):
second_factor_list.append(i)
if len(second_factor_list) > d:
second_factor_list = second_factor_list[:d]
first = int(''.join(first_factor_list))
second = int(''.join(second_factor_list))
next_num = first - second
print(next_num)
The following code runs fine for b = 7 and d = 20.
Output :
19999999999999999993
12000000000000000006
13920000000000000002
14276352000000000001
14285708150046720001
14285714285711650466
14285714285714285715
14285714285714285715
The answer obtained in the end is correct and also the rate of convergence is quadratic.
In fact this code gives the correct answer for b = 3,4,5,6,7 while keeping d = 20 and the initial guess 0.1
However the following code goes in an infinite loop for all other values of b.
I have tried making several changes to the code but haven’t been able to solve this. I couldn’t find such an implementation on the internet either. Please help me in solving this issue.
Thank you.