Using Topological sort v/s using DFS

help
,
1

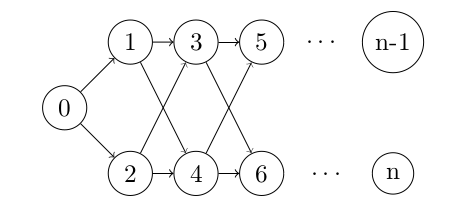
Question:

image
image1238×386 49.8 KB

Link to question: Lonely Island | Practice Problems

My question is what suggests that we’ve to use topo sort in this question? Why is my following DFS approach incorrect?

double prob[MAX];
int outdegree[MAX];
void DFS(vi adj[], int s, double parent_probability_through_this_path){
for(int i = 0; i < adj[s].size(); i++){
    prob[adj[s][i]] += parent_probability_through_this_path*(1.0/outdegree[s]);
    DFS(adj, adj[s][i], parent_probability_through_this_path*(1.0/outdegree[s]));
}

}
Full code: Submission (33961586) for Lonely Island | HackerEarth
I am simply adding all possible paths of reaching a node. There may be multiple paths to a node and hence I am not checking the visited condition. When a node is visited again, I simply add the prob of reaching here through this DFS path to the probability that existed by already visiting it through some other DFS path.This is only passing a few TCs.

PS: vi is vector. Calling function like this
prob[r] = 1;
DFS(adj, r, 1.0);
What’s the flaw in logic?

2

Your solution would indeed give the correct answer. However in this case the limiting factor would be time. Imagine the following graph:

image

Your algorithm would then have efficiency \mathcal{O}(2^n) while the algorithm using Topological sort would be \mathcal{O}(n).
In other words your solution would get Time Limit Exceeded

3

can you elaborate?