Can someone explain first test case for this problem
Thanks in advance.
3
0 0 4
5 0 4
-5 0 4
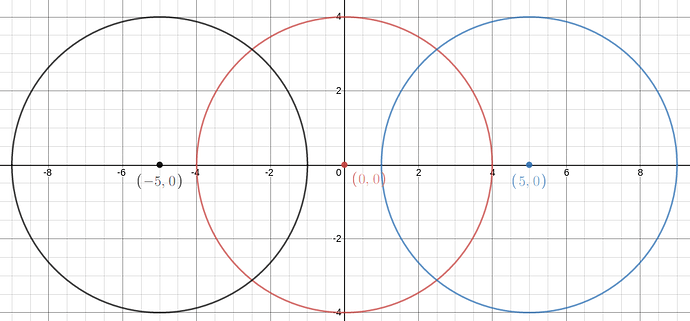
This is the visualisation of the first test case.
Hence, to cover the maximum area, we select the black crane and the blue crane as shown in diagram.
Area of a circle is given by \pi r^2.
Here, maximum possible area or A = \pi r_2^2 + \pi r_3^2
We need to report B, where
B = \dfrac{A}{\pi} = \dfrac{ \pi r_2^2 + \pi r_3^2}{\pi}=\dfrac{\pi (r_2^2 +r_3^2 )}{\pi} = r_2^2 +r_3^2
Hence, for this case B = 4^2 + 4^2 = 32.
in this u have to find the maximum sumof r^2 and also see that no two cranes collide … simply use dynamic programming in this …
i thought about greedy approach but it will not work everytime
also to see whether the two cranes are valid … ;
just use this
r1 + r2 >=( (x1-x2)^2 + (y1-y2)^2 )^1/2
soon i will send the code … rest for now this is the logic