PROBLEM LINK:
Author: Leo Lee
Tester: Daanish Mahajan
Editorialist: Leo Lee
DIFFICULTY:
Easy
PREREQUISITES:
None
PROBLEM:
A city has N vertical roads numbered 1, 2, ..., N from left to right, each spaced 1 unit apart; similarly, there are M horizontal roads numbered 1, 2, ..., M from bottom to top, each spaced 1 unit apart. We will denote the intersection between the x-th vertical road and the y-th horizontal road as (x, y).
You have to make K deliveries, with the i-th delivery starting at (x_i, y_i) and ending at (x'_i, y'_i). You can also travel every road with speed 0.5 (meaning it would take him 2 units of time to travel 1 unit of distance). However, you can also change exactly one horizontal road to a highway, meaning the speed on that road would increase to 1.
You want to choose a road to be a highway such that the sum of durations of all the deliveries is minimum possible. Find this minimum sum.
Note that each delivery starts exactly at (x_i, y_i) and ends at (x'_i, y'_i), i.e., we don’t count the time taken to travel from (x'_{i-1}, y'_{i-1}) to (x_i, y_i) in our answer.
Subtask 1 [17 points]: 1 \le N, M, K \le 10^5, y_i = y_{i-1} for all i>0.
Subtask 2 [34 points]: 1 \le N \le 10^5, K \le 10.
Subtask 3 [49 points]: 1 \le N, M, K \le 10^5
QUICK EXPLANATION:
We consider each possible horizontal road. For each road, there are 5 possible categories of deliveries: too low, increasing, middle, decreasing, too high. We can calculate the maximum amount we are saving per each road by iterating through each road and maintaining how many deliveries are in each category. We can then subtract this from the total cost (the Manhattan distance of every delivery times two).
EXPLANATION:
Subtask 1:
If all y_i are equal, that means we can use the y_0 th horizontal road for every delivery. Since every delivery can use the road, it is optimal to choose the y_0 th horizontal road to be a highway. The answer is then the sum of (|x_i - x'_i| + 2 * |y_i - y'_i|) across all i.
Subtask 2:
Note that the direction of travel doesn’t matter. For simplicity, we will assume y_i \le y'_i, since we can swap the start and end points if otherwise.
For each delivery, we can calculate the minimum time it takes to complete it when the highway is given.
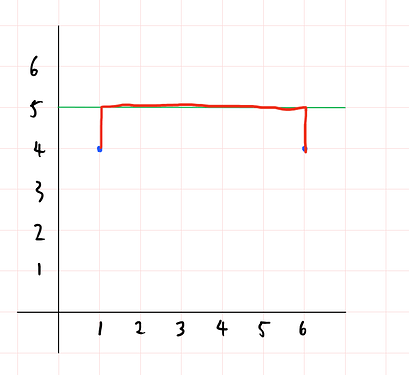
Consider the delivery from (1, 4) to (6, 4).
If we don’t have a highway, the time taken would be 2(|4-4|+|6-1|) = 10.
However, we can reduce the time taken to 5 by setting the 4th horizontal road as a highway:
However, this is not the only highway we can choose to reduce the duration of this delivery. We can also choose the 5th horizontal road to be a highway, which would make the delivery take 5+2*1+2*1 = 9 units of time, which is still smaller than the initial time of 10.
Note that there was a horizontal detour of 4 to make use of this highway.
Similarly, we can set the 3rd horizontal road to be a highway as well:
However, can we set the 2nd horizontal road to be a highway and still achieve a reduction in time taken? If we use this highway, the time taken is now 5+2*2+2*2=13, which is greater than the initial value of 10. This means that if there was a highway on the 2nd horizontal road, it is better off not taking it.
Indeed, we can see that there is a range of highways we can use for there to be a reduction in time for this delivery. If there is a highway outside this range, it is faster to not use it.
Now let’s consider the delivery (1, 4) to (6, 2). Using a similar logic as above, we can see that using highways 1 to 5 saves the time taken. Notice, however, that for highways 1 and 5, we need to make a vertical detour, while we don’t need to for 2 to 4.
We will call the three shades States A, B and C respectively (bottom to top) to help with the explanation.
Now, we can generalise this observation to any delivery. Let’s define the highway as the H th horizontal road.
If we don’t use the highway, the time would be 2(|x_i - x'_i| + |y_i - y'_i|).
If we do use the highway, there are three possibilities:
-
State A: If H < y_i, we need to make a detour down. Specifically, we can travel down from y_i to H, travel horizontally, go back up to y_i, then travel up to y'_i. Since we made a detour of distance y_i - H both ways, it will cost us 4(y_i -H) time. Therefore, the total taken is |x_i - x'_i| + 2*|y_i - y'_i| + 4(y_i -H).
-
State B: If y_i \le H \le y'_i, there is no need to take a detour. We can travel up from y_i to H, travel horizontally then travel up to y'_i. The time taken is |x_i - x'_i| + 2*|y_i - y'_i|.
-
State C: Similarly to above, if H > y'_i, we need to make a detour up. The total time taken here is |x_i - x'_i| + 2*|y_i - y'_i| + 4(H - y'_i).
We can therefore iterate through each road and check the minimum time it takes for each of the deliveries. Since we need to check all deliveries for all roads, this solutions runs in O(MK) time.
Subtask 3:
For each delivery, we can calculate the range of roads such that turning the road into a highway would decrease the total time. For taking the highway H to be beneficial, the time reduction for the horizontal road has to be greater than the vertical detour we are taking.
This means that |x_i - x'_i| > 4(y_i - H) and |x_i - x'_i| > 4(H - y'_i).
Rearranging this gives us (y_i - \frac{|x_i-x'_i|}{4}) \le H \le (y'_i + \frac{|x_i-x'_i|}{4}).
Therefore, for each package, we can keep track of where each package enters State A, enters State B, enters State C and exits State C.
This means that we can simply iterate through all the possible horizontal roads from 1 to M, keeping a count of the number of roads in each State. This can be done by handling entries and exits, calculating the initial saving then adding it onto the time saved when taking that road.
Now, let’s quickly consider the delivery from (1, 6) to (10, 4). If we draw the routes for each of the possible highway selections, it looks like this:
We can see that the time saved increases in State A, stays the same in State B and decreases in State C.
For every package in State A, the time saved we get from taking highway H+1 instead of H is increased by 4, as the detour distance is decreased by 2 (1 both ways). Similarly, for every package in State C, the time saved is decreased by 4. For packages in State B, there is no difference as there is no detour.
Therefore, we can handle the increase and decrease in time saved according to the number of roads that are in State A and State C. We add 4A and -4C to our time saved, where A is the number of packages in State A and C is the number of packages in State C respectively.
From this, we can keep a running maximum of the total time saved we get from each road. We can then subtract this maximum time saved from the cost of not taking any highway, i.e 2(|x_i - x'_i| + |y_i- y'_i|) for all i.
This solution runs in O(M+K), which is enough to pass this subtask and therefore the full problem. For implementation details, please refer to the commented code below.
SOLUTIONS:
Setter's Solution
#pragma region cp-helper
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define nl '\n'
#define fileio(in, out) freopen(in, "r", stdin); freopen(out, "w", stdout)
#define io ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0)
const int mod = 1000000007;
const int mod2 = 998244353;
#pragma endregion
const int N = 100005;
int n, m, k, incoming, outgoing, inside, ans, cost, saving;
struct deli {
int x1, y1, x2, y2;
};
deli arr[N];
vector<int> in[N], out[N], rin[N], rout[N];
signed main() {
io;
cin >> n >> m >> k;
for (int i=0; i<k; i++) {
cin >> arr[i].x1 >> arr[i].y1 >> arr[i].x2 >> arr[i].y2;
if (arr[i].y1 > arr[i].y2) {
swap(arr[i].x1, arr[i].x2);
swap(arr[i].y1, arr[i].y2);
}
cost += 2 * (abs(arr[i].x1 - arr[i].x2) + abs(arr[i].y1 - arr[i].y2));
int dist = abs(arr[i].x1 - arr[i].x2) / 4; // maximum detour
// lowest y where it is profitable
int l = max(0ll, arr[i].y1 - dist);
// highest y where it is profitable
int r = min(m+1, arr[i].y2 + dist);
in[l].push_back(i); // when to insert it into group
out[r].push_back(i); // when to exit
rin[arr[i].y1].push_back(i); // last index that increases
rout[arr[i].y2].push_back(i); // 1 before first index that decreases
}
// add all roads that starts increasing at 0 and below
for (auto j : in[0]) {
incoming++;
saving += abs(arr[j].x1 - arr[j].x2) - 4 * arr[j].y1;
}
for (int i=1; i<=m; i++) {
// consider taking this road
// first, handle increases and decreases of deliveries that was already added
saving += 4 * incoming; // for each road that is increasing, the 'profit' is increased by 4
saving -= 4 * outgoing; // same but reverse
// then, insert deliveries that start increasing here
for (auto j : in[i]) {
incoming++;
saving += abs(arr[j].x1 - arr[j].x2) - 4 * abs(i - arr[j].y1);
}
// 'saving' here is the amount we save when we take this road
// so maintain maximum
ans = max(ans, saving);
// then, insert roads that start decreasing from next road onwards
outgoing += rout[i].size();
// then, remove roads that stop increasing from next road onwards
incoming -= rin[i].size();
// then, remove roads that stop being profitable from next road onwards
for (auto j : out[i]) {
outgoing--;
saving -= abs(arr[j].x1 - arr[j].x2) - 4 * abs(i - arr[j].y2);
}
}
// final answer is cost without taking anything minus saving by taking one road
cout << cost - ans << endl;
}
Tester's Solution
import java.util.*;
import java.io.*;
public class Main{
static PrintWriter out;
static InputReader in;
public static void main(String args[]){
out = new PrintWriter(System.out);
in = new InputReader();
new Main();
out.flush(); out.close();
}
Main(){
solve();
}
final int max = 100005;
class pair{
int F, S, T;
pair(int a, int b, int c){
F = a; S = b; T = c;
}
public String toString(){
return F + " " + S + " " + T;
}
}
ArrayList<pair> al = new ArrayList<>();
ArrayList<pair> down = new ArrayList<>();
ArrayList<pair> up = new ArrayList<>();
pair x[] = new pair[max], y[] = new pair[max];
long ans[] = new long[max];
void solve(){
int n = in.nextInt(), m = in.nextInt(), k = in.nextInt();
long tot = 0;
for(int i = 0; i < k; i++){
int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 = in.nextInt();
tot += 2 * (Math.abs(x1 - x2) + Math.abs(y1 - y2));
al.add(new pair(Math.min(y1, y2), i, 2)); al.add(new pair(Math.max(y1, y2) + 1, i, 1));
x[i] = new pair(Math.min(x1, x2), Math.max(x1, x2), -1);
y[i] = new pair(Math.min(y1, y2), Math.max(y1, y2), -1);
}
Collections.sort(al, (A, B) -> A.F == B.F ? A.T - B.T : A.F - B.F);
long pvt = 0; int ptr = 0;
for(int i = 1; i <= m; i++){
while(ptr < 2 * k && al.get(ptr).F == i){
pair p = al.get(ptr);
int gap = x[p.S].S - x[p.S].F;
if(p.T == 2){
pvt += gap;
down.add(new pair(p.F - 1, p.S, 2));
down.add(new pair(p.F - gap / 4 - 1, p.S, 1));
}else{
pvt -= gap;
up.add(new pair(p.F, p.S, 2));
up.add(new pair(p.F + gap / 4, p.S, 1));
}
ptr++;
}
ans[i] = -pvt;
}
Collections.sort(down, (A, B) -> A.F == B.F ? A.T - B.T : B.F - A.F);
Collections.sort(up, (A, B) -> A.F == B.F ? A.T - B.T : A.F - B.F);
long xt = 0, yt = 0, cnt = 0;
ptr = 0;
for(int i = max - 1; i >= 0; i--){
while(ptr < down.size() && down.get(ptr).F == i){
pair p = down.get(ptr);
int gap = x[p.S].S - x[p.S].F;
if(p.T == 2){
xt += gap; yt += y[p.S].F; cnt++;
}else{
xt -= gap; yt -= y[p.S].F; cnt--;
}
ptr++;
}
ans[i] += 4 * (yt - cnt * i) - xt;
}
cnt = 0; xt = 0; yt = 0; ptr = 0;
for(int i = 0; i < max; i++){
while(ptr < up.size() && up.get(ptr).F == i){
pair p = up.get(ptr);
int gap = x[p.S].S - x[p.S].F;
if(p.T == 2){
xt += gap; yt += y[p.S].S; cnt++;
}else{
xt -= gap; yt -= y[p.S].S; cnt--;
}
ptr++;
}
ans[i] += 4 * (cnt * i - yt) - xt;
}
long rs = Long.MAX_VALUE;
for(int i = 0; i < max; i++){
rs = Math.min(tot + ans[i], rs);
}
out.println(rs);
}
public static class InputReader{
BufferedReader br;
StringTokenizer st;
InputReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public int nextInt(){
return Integer.parseInt(next());
}
public long nextLong(){
return Long.parseLong(next());
}
public double nextDouble(){
return Double.parseDouble(next());
}
public String next(){
while(st == null || !st.hasMoreTokens()){
try{
st = new StringTokenizer(br.readLine());
}catch(IOException e){}
}
return st.nextToken();
}
}
}