I was solving this problem and got 100 points.
This submission ran in 0.98s as seen below. I sorted the vector, considered every pair a[i], a[j] with i < j. Then using their common difference, I checked if the next value exists with the help of binary search (basic Arithmetic progression).
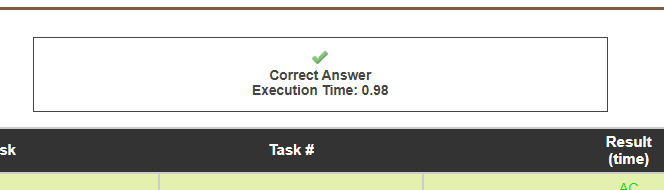
Since this is very slow (1 second time limit), I decided to try to use pragmas to decrease runtime. I don’t know much about that so I failed to get 100 points. I decided to submit my code without pragmas (the original submission). It ran in 0.99s.
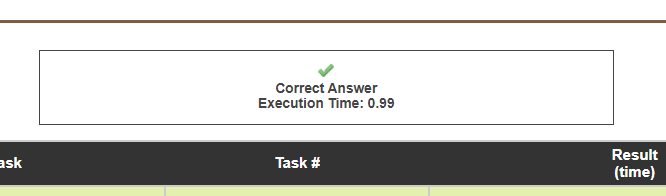
I don’t know why the exact same submission ran slower. Can someone please explain this?
For the most important part, I was annoyed about my code being slow. I decided to use unordered_map. I began to doubt the test cases. My solution with unordered_map got accepted in 0.36s which is almost 3x faster.
I blew up unordered_map.
I created an input file with 2500 occurrences of 99733 using this simple python code:
f = open("test.txt", "a")
s = "2500 "
for i in range(2500):
s += "99733 "
f.write(s)
f.close()
The same solution which ran in 0.36s is running since 10 minutes.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define ll long long
using namespace __gnu_pbds;
using namespace std;
template <class T> using oset = tree <T, null_type, less <T>, rb_tree_tag, tree_order_statistics_node_update>;
void usaco(string name = "")
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
if(name.size())
{
freopen((name+".txt").c_str(), "r", stdin);
freopen((name+".out").c_str(), "w", stdout);
}
}
int main()
{
usaco("test");
int n, ans = 1;
cin >> n;
vector <int> a(n);
unordered_map <int, int> m;
for (int i = 0; i < n; ++i) cin >> a[i], ++m[a[i]];
sort(begin(a), end(a));
for (int i = 0; i < n-1; ++i)
{
for (int j = i+1; j < n; ++j)
{
int d = a[j]-a[i];
int cur = a[j]+d;
int t = 2;
while (m[cur])
{
++t;
cur += d;
}
ans = max(ans, t);
}
}
cout << ans << '\n';
}
This shows how bad the test cases are. Anything above O(n^2) should not pass according to the constraints. Is it possible for the solutions to be rejudged?
Also, does anyone know how to do it in O(n^2)? ![]()