PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Daanish Mahajan
Tester & Editorialist: Taranpreet Singh
DIFFICULTY
Easy-Medium
PREREQUISITES
Combinatorics
PROBLEM
You are given a tree with N nodes numbered from 1 to N. A set S of nodes is called valid if there exist two vertices u and v (possibly, u=v) such that every node in S lies on the simple path from u to v.
Count the number of valid sets modulo 10^9+7. Two sets are different if one node is included in one set and not in the other. If there are multiple pairs (u, v) making a set valid, that set is still only counted once.
QUICK EXPLANATION
- For each node, find the number of ways to select a subset of nodes in subtree of the node, such that all nodes can lie on a single path starting from that node. Let’s call these paths as downward paths
- All paths in tree can be seen as combination of at most two such downward paths starting from a single node and going into different children subtrees.
EXPLANATION
Let’s consider this problem subtask by subtask.
Subtask 1
Let us think of the shortest path covering a given subset. We can prove that such path would be unique for a chosen subset and shall have both of its endpoints inside the subset. If not, we can further remove nodes on endpoint which is not included.
Hence, if we denote value of a path (u, v) as 2^{L-2} where L is the number of nodes on simple path from u to v if u \neq v and 1 if u = v, the answer to the original problem is the sum of values of paths over all unordered pairs (u, v).
Why?
Let’s group subsets by the endpoint pair of shortest path containing all the nodes of subset. Let’s assume pair (u, v) is the shortest path, and has total L nodes including u and v.
Now, both u and v must be in subset, but remaining L-2 nodes may or may not be inside subset. Hence, there would be 2^{L-2} subsets having (u, v) as the shortest path containing the subset.
Note that this holds only when u \neq v. In case u = v, Only subset is \{u\}
Hence, for solving subtask 1, we can try all pairs of paths, compute distances in order to quickly compute values. Excluding the value of paths (u, u), each path might be included twice depending upon implementation.
We can also try rooting the tree at node u and summing the value of paths from root to each node. This way, the depth of other endpoint would directly give the distance from root node.
Subtask 2
While the idea of summing the value of paths is good, we need to sum the value of paths in better than O(N^2).
Now, let’s root the tree at any node, and group the paths by the node having least depth among nodes lying on the path. We can see that for path (u, v), such node would be unique, and would be the Lowest Common Ancestor of u and v, say lca. For now, assume lca node is not u or v node.
Let’s consider following tree
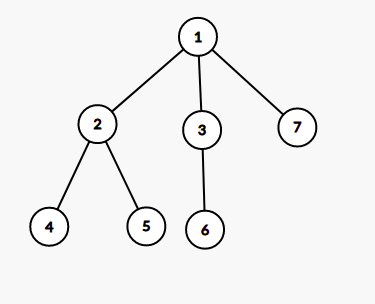
Let’s count the sum of values of paths, which have node 1 as lca node. All paths can be of two types.
- lca node is one of the endpoint
- Two chains start from lca node and end in different child subtrees
Let’s denote f(u) as the sum of values of paths starting from node u and ending in subtree of node u, where node u may or may not be selected, but node v is selected. Let’s refer to this as modified value.
Why defining new value: The benefit of using this definition is that we don’t need to multiply value sums by 2 when u no longer remains endpoint (when some path is joined at node u)
For the paths having lca as one endpoint, It’ll either be single node lca node path, or it will go into one of the child’s subtree. Let’s say immediate child ch is the child where the path ends. All paths starting from ch and ending in subtree of ch can be extended to include lca node.
For child ch, f(ch) denotes the sum of values paths in subtree of ch, which can be extended to end at lca node. Hence, the number of such paths is \displaystyle 1 + \sum_{ch \in child(u)} f(ch). Also, It is easy to see that \displaystyle f(u) = 1 + 2*\sum_{ch \in child(u)} f(ch)
Now, for paths not having lca node as endpoint, it shall be equivalent to selecting two children of lca node, and pair one chain in child one’s subtree with one chain in second child’s subtree. Say ch1 and ch2 are chosen. The sum of values of pairs of chains would be f(ch1)*f(ch2). Hence, we need to compute \displaystyle \sum_{ch1, ch2 \in child(u), ch1 < ch2} f(ch1)*f(ch2).
All these represent the subsets, but doesn’t account for the lca node. lca node can either be included or not for each pair of chain. Hence, the sum of values of paths of second type becomes \displaystyle 2* \sum_{ch1, ch2 \in child(u), ch1 < ch2} f(ch1)*f(ch2).
This quantity is easy to compute by considering children of u one by one and maintaing sum being sum of f(ch) for all children of u already considered.
Hence, we have computed the sum of values of paths of both types, and also computed f(u). Hence, we can solve this problme by a single DFS.
In case of doubts, please refer my implementation 1, which uses the same ideas line by line, and same variable names.
If interested, see an alternate implementation and try to prove how it works.
TIME COMPLEXITY
The time complexity is O(N) per test case.
SOLUTIONS
Setter's Solution
#include <sys/resource.h>
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int maxt = 5;
const int mod = 1e9 + 7;
long long ans = 0;
long long dp[100010];
vector<int> g[100010];
long long add(long long a, long long b){
a += b;
if(a >= mod)a -= mod;
return a;
}
long long mul(long long a, long long b){
a *= b;
if(a >= mod)a %= mod;
return a;
}
void dfs(int u, int pa){
long long sum = 0;
for(int v : g[u]){
if(v == pa)continue;
dfs(v, u);
ans = add(ans, add(mul(sum, mul(dp[v], 2)), dp[v]));
sum = add(sum, dp[v]);
}
dp[u] = add(mul(2, sum), 1);
}
int main()
{
rlimit R;
getrlimit(RLIMIT_STACK, &R);
R.rlim_cur = R.rlim_max;
setrlimit(RLIMIT_STACK, &R);
int t; cin >> t;
int n;
while(t--){
cin >> n;
for(int i = 0; i <= n; i++){
g[i].clear(); dp[i] = 0;
}
int u, v;
for(int i = 0; i < n - 1; i++){
cin >> u >> v;
g[u].pb(v); g[v].pb(u);
}
ans = n;
dfs(1, 0);
cout << ans << endl;
}
}
Tester's Solution
import java.util.*;
import java.io.*;
class VPATH{
//SOLUTION BEGIN
long MOD = (long)1e9+7;
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni();
int[] from = new int[N-1], to = new int[N-1];
for(int i = 0; i< N-1; i++){
from[i] = ni()-1;
to[i] = ni()-1;
}
int[][] g = make(N, from, to);
long[] f = new long[N];
pn(dfs(g, f, 0, -1));
}
long dfs(int[][] g, long[] f, int u, int p){
long ans = 0;
//Computing f(u) for children
for(int v:g[u])if(v != p){
ans += dfs(g, f, v, u);
if(ans >= MOD)ans -= MOD;
}
long sum = 0;
for(int v:g[u]){
if(v == p)continue;
ans += (sum*f[v]*2)%MOD;//pairing chain in subtree of child v with chains in subtrees of previous children
sum += f[v];//current child is added, to be considered for pairing with next children
if(ans >= MOD)ans -= MOD;
if(sum >= MOD)sum -= MOD;
}
ans += sum+1;//sum is the number of paths with u as endpoint and v in subtree of any of its children, 1 is for path (u, u)
if(ans >= MOD)ans -= MOD;
f[u] = (2*sum+1)%MOD;//For each path in subtree of u, node u may or may not be included, hence 2*sum. One is added for path having lower endpoint u
return ans;
}
int[][] make(int N, int[] from, int[] to){
int[] cnt = new int[N];
for(int x:from)cnt[x]++;
for(int x:to)cnt[x]++;
int[][] g = new int[N][];
for(int i = 0; i< N; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< N-1; i++){
g[from[i]][--cnt[from[i]]] = to[i];
g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new VPATH().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Tester's Alternate Implementation
import java.util.*;
import java.io.*;
class VPATH{
//SOLUTION BEGIN
long MOD = (long)1e9+7;
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni();
int[] from = new int[N-1], to = new int[N-1];
for(int i = 0; i< N-1; i++){
from[i] = ni()-1;
to[i] = ni()-1;
}
int[][] g = make(N, from, to);//building tree's adjacency list
long[] DP = new long[N];
//DP[u] -> Number of subsets in subtree of u such that for all subsets, there exists atleast one path
//starting from u,
//ending in subtree of u,
//contains all values present in subset on path
//endpoint v of that path is in subset
pn(dfs(g, DP, 0, -1));
}
long dfs(int[][] g, long[] DP, int u, int p){
long ans = 0;
for(int v:g[u])if(v != p){
ans += dfs(g, DP, v, u);
if(ans >= MOD)ans -= MOD;
}
long w0 = 0, w1 = 1;
ans++;
for(int v:g[u]){
if(v == p)continue;
ans += (w0+w1)*DP[v]%MOD;
w0 += DP[v];
w1 += DP[v];
if(ans >= MOD)ans -= MOD;
if(w0 >= MOD)w0 -= MOD;
if(w1 >= MOD)w1 -= MOD;
}
DP[u] = w0+w1;
if(DP[u] >= MOD)DP[u] -= MOD;
return ans;
}
int[][] make(int N, int[] from, int[] to){
int[] cnt = new int[N];
for(int x:from)cnt[x]++;
for(int x:to)cnt[x]++;
int[][] g = new int[N][];
for(int i = 0; i< N; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< N-1; i++){
g[from[i]][--cnt[from[i]]] = to[i];
g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new VPATH().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()
